【C++要笑着学】搜索二叉树 (SBTree) | K 模型 | KV 模型

文章列表

C++ 表情包趣味教程 👉 《C++要笑着学》

💭 写在前面：半年没更 C++ 专栏了，上一次更新还是去年九月份，被朋友催更很久了hhh

本章倒回数据结构专栏去讲解搜索二叉树，主要原因是讲解 map 和 set 的特性需要二叉搜索树做铺垫，理解搜索二叉树有助于更好地理解 map 和 set 的特性。第二个原因是为了后期讲解查找效率极高的平衡搜索二叉树，随后再讲完红黑树，我们就可以模拟实现 map 和 set 了。二叉树的基础知识讲解在我的《树锯结构》专栏中有写，这里放上链接方便复习。

🔗 复习链接：【数据结构】二叉树的遍历

Ⅰ. 搜索二叉树（SearchBinaryTree）

0x00 搜索二叉树的概念

📚 概念：搜索二叉树又称为二叉排序树，它或者是一颗空树，或者是具有以下性质的二叉树：

若其左子树不是空，则左子树上所有节点的值都小于根结点的值
若其右子树不是空，则右子树上所有结点的值都大于根结点的值
其左右子树必须都是二叉搜索树

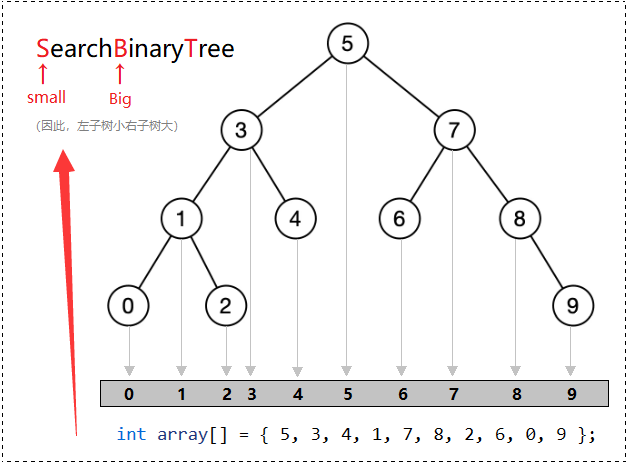
至于叫它 "搜索二叉树"，还是 "二叉搜索树"，这个似乎也没有特别的规定，应该都是可以的。

但我更喜欢叫它 "搜索二叉树"，因为这样翻译过来是 "Search Binary Tree"，

但是我并不是因为这样可以叫它 SB 树才喜欢的。

（而且这样也不文明，而且已经有 SB 树了，Size Balanced Tree）

而是因为叫 "搜索二叉树 Search Binary Tree" 可以顺便记住它的性质：

Search Binary Tree，S 也可以表示 Small，B 也可以表示 Big，SB 即左边小右边大！

（一般而言，搜索二叉树都是左边小右边大的）

这样可以正好能对应它的性质：左子树的值 < 根 < 右子树的值

🔺 结论：任意一个子树都需要满足，左子树的值 < 根 < 右子树的值，才能构成二叉搜索树。

0x01 搜索二叉树的优势

既然叫搜索二叉树，它肯定是用来搜索的，当满足搜索二叉树时你将可以快速地查找任意的值。

💭 举个例子： 查找 $7$

放到以前我们如果不用二分查找，可能会选择用暴力的方式去从头到尾遍历一遍。

但现在学了搜索二叉树，我们就可以轻松找到这个 $7$ 了，不信你看：

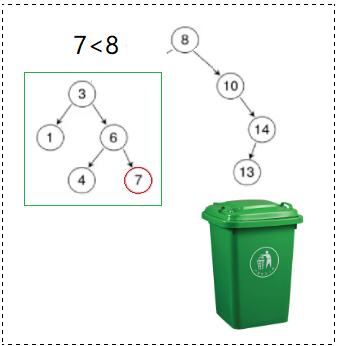
STEP1： $7$ 比 $8$ (根节点) 小，根据搜索二叉树的性质，它必然不会出现在右子树 (右边大) ！

所以，直接 🔒 锁定左子树开始找：

STEP2： $7$ 比 $3$ 大，根据性质它肯定不会出现在左子树 (左边小) ！

这次，直接 🔒锁定 右子树继续找：

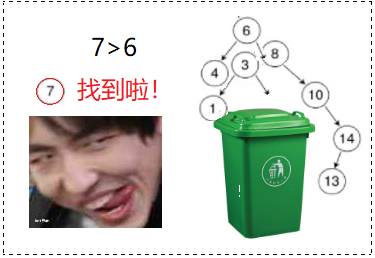
STEP3： 我们继续对比， $7$ 比 $6$ 大，所以在右边，就这么轻轻松松的找到了：

搜索二叉树查找一个值的最坏情况，也只是查找高度次。你就说爽不爽吧。

这就是搜索二叉树，它的搜索功能是真的名副其实的厉害！

0x02 二叉搜索树的时间复杂度：O(N)

上面的例子举得太丝滑了，会让人误以为搜索二叉树的时间复杂度是 $O(logN)$ ……

但实际上是 $O(N)$ ！！！

因为这棵树是有可能会蜕化的，极端情况下会蜕化成一个 "单边树" ：

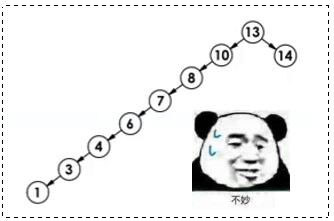
😢 最差情况：二叉搜索树退化为单边树（或类似单边），其平均比较次数为：

$O(\\frac{N}{2})\\Rightarrow O(N)$

但是在好的情况下，其搜索效率也是非常可观的：

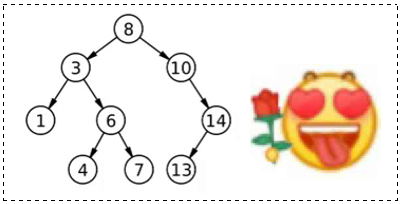
😍 最优情况：二叉搜索树为完全二叉树（或接近完全二叉树），其平均比较次数为：

$O(log_2N)\\Rightarrow O(logN)$

对于时间复杂度的分析我们要做一个悲观主义者，根据最差情况去定时间复杂度。

🔺 总结：搜索二叉树的时间复杂度为 $O(N)$

0x03 搜索二叉树的改良方案

如果搜索二叉树蜕化成了单边树，其性能也就失去了，能否进行改进让它保持性能？

如何做到不论按照上面次序插入关键码，二叉搜索树的性能均能达到最优？

搜索二叉树由于控制不了极端情况，与 $O(logN)$ 失之交臂，但平衡二叉搜索树做到了。

"平衡二叉树的搜索效率极高"

严格意义上来说满二叉树才是 $O(logN)$ ，完全二叉树是接近 $O(logN)$ 。

而平衡搜索二叉树维持左右两边均匀程度，让它接近完全二叉树，从而让效率趋近 $O(logN)$ 。

Ⅱ. 搜索二叉树的实现

0x00 搜索二叉树的定义

搜索二叉树，SearchBinaryTree 名称实在是又臭又长！

我们不如取名为 SBTree，但是 SBTree 听起来好像有点不文明，我们还是叫 BSTree 吧。

这里我们用模板，模板参数我们给了一个 $K$ ，表示 key 的意思（模板参数并非一定要用 T）。

template<class K> 
struct BSTreeNode {BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key): _left(nullptr), _right(nullptr), _key(key) {}
};

下面我们来定义整个树，BSTreeNode 也有些长了，我们不如将其 typedef 成 Node 。

这里我们构造函数都没必要写，它自己生成的就够用了：

template<class K> 
class BSTree {typedef BSTreeNode<K> Node;
private:Node* _root = nullptr;    // 懒得写构造函数了
};

0x01 搜索二叉树的插入

我们先来实现最简单的插入操作：

如果树为空，则直接新增结点，赋值给 root 指针。
如果树不为空，按二叉搜索树性质查找插入位置，插入新节点。

bool Insert(const K& key);

Insert 的实现我们可以用递归，也可以用非递归，这一块递归比非递归更难理解。

秉着先难后易的态度，我们先讲比较难理解的非递归版本！

💡 分析

Step1：首先检查是否有根结点 _root，如果没有我们就 new 一个结点出来作为根结点。
此时插入成功，返回 true。

Step2：插入就需要找到插入位置，我们定义一个 cur 变量，从根节点开始，
根据搜索二叉树 "SB" 性质，将 cur 结点的值与插入的值 $x$ 进行大小比较。

如果插入的值大于当前结点值，则将 cur 结点向右移动 cur=cur->_right ；
如果插入的值小于当前节点值，就将 cur 结点向左移动 cur=cur->_left。

值得注意的是，我们还需要额外记录一下 cur 的父结点，因为你不知道什么时候会碰 $\\textrm{null}$ 结束。
并且当我们找到插入位置后，仅仅 new 上一个新结点给 cur 是完成不了插入操作的！
因为直接这么做 cur 也只是一个局部变量而已，你需要 cur 跟上一层（cur 的父亲）相链接才行！
为了能找到上一层，所以我们还需要额外定义一个 prev 变量来记录 cur 的父结点，
在我们更换 cur 结点时记录父结点的位置 prev=cur 即可。
当然了，还有一种插入失败的情况，就是判断大小时出现等于的情况，返回 false 即可。
（重复的值是不允许插入的，默认情况是不允许冗余的！但是也有针对这个的变形，后续再说）

Step3：插入！new 一个新结点给 cur，此时 cur 只是一个局部变量，必须要和父亲链接，
此时应该链接父亲的左边，还是链接父亲的右边？我们不知道，所以我们需要再做一个比较！

如果父节点的值大于插入的值，则将 cur 链接到父亲左边 prev->_left=cur；
反之将 cur 链接到父亲右边 prev->_right=cur。

最后，插入成功返回 true，我们的插入操作就大功告成了。

💬 代码演示：Insert 接口的实现

/* 插入 */
bool Insert(const K& x) {/* 检查是否由根节点 */if (_root == nullptr) {    // 如果根节点为空指针_root = new Node(x);   // 创建一个新结点作为根结点return true;           // 插入成功，返回真}Node* prev = nullptr;      // 用于记录cur的父亲Node* cur = _root;         // 从根节点开始/* 找到插入位置 */while (cur != nullptr) {if (x > cur->_key) {          // 如果插入的值大于当前结点值，则向右移动prev = cur;               // 保存父节点cur = cur->_right;        // 令cur右滑}else if (x < cur->_key) {     // 如果插入的值小于当前结点值，则向左移动prev = cur;      cur = cur->_left;         // 令cur左滑}else {                        // 相等的情况，禁插return false;             // 插入失败，返回假}}/* 插入位置已找到，准备进行链接操作 */cur = new Node(x);      // 创建一个新结点，赋给cur，此时cur为局部，需与父结点链接if (prev->_key > x) {   // 如果父结点的值大于插入的值，则将cur链接到左边prev->_left = cur;} else {                  // 如果父节点的值小于插入的值，则将cur链接到右边prev->_right = cur;}return true;   // 插入成功，返回真
}

再写一个中序遍历来测试一下插入的效果：

void InOrder(Node* root) {if (root == nullptr) {return;}InOrder(root->_left);            // 左cout << root->_key << " ";       // 值InOrder(root->_right);           // 右
}

模拟出一个测试用例：

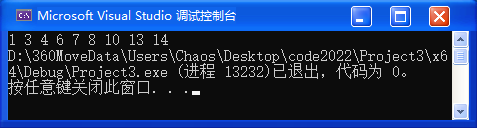
void TestBSTree() {BSTree<int> t;int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };for (auto e : a) {t.Insert(e);}t.InOrder();  ❌ 没法传根
}

此时会出现一个问题，因为根是私有的，我们没办法把根传过去。

此时我们可以选择在类内部写一个成员函数 GetRoot 去取根，但是这里我们可以选择这么做：

	void InOrder() {_InOrder(_root);}private:// 改为内部函数void _InOrder(Node* root) {if (root == nullptr) {return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;
};

干脆将刚才我们实现的中序设为 private 私有，然后再写一个 InOrder 放在公有的区域。

这就是在类内访问 _root 了，没有什么问题。

如此一来我们在类外就可以直接调用 InOrder，并且也不需要传递参数了。

int main(void)
{TestBSTree();return 0;
}

🚩 运行结果：

0x02 搜索二叉树的查找

find 实现很容易，用和刚才一样的思路，从根结点开始查找。

从根开始，如果要查找的值大于 cur 目前的值，则让 cur 往右走，反之往左走。

当查找得值与 cur 的值相等时则说明找到了，返回 true。

当 cur 触及到空（while 循环结束）则说明找不到，返回 false。

💬 代码实现：搜索二叉树的查找

/* 查找 */
bool Find(const K& target) {Node* cur = _root;                    // 从根结点开始查找while (cur != nullptr) {      if (target > cur->_key) {         // 如果目标值比当前结点值大，cur↘cur = cur->_right;       }else if (target < cur->_key) {    // 如果目标值比当前结点值小，cur↙cur = cur->_left;}else {                            // 如果目标值等于结点值，说明找到了/* 找到了，返回真 */return true;}}/* 没找到，返回假 */return false;
}

0x03 搜索二叉树删除

搜索二叉树真正困难的是删除，搜索二叉树删除的实现是有很有难度的。

删除的实现就需要一些 "奇技淫巧" 了，断然删除会毁树。

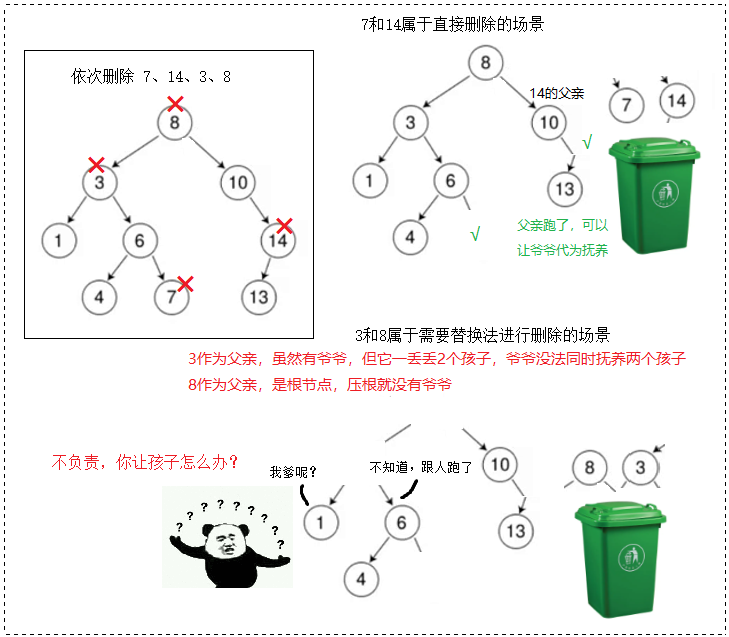
没有孩子或者只有一个孩子，可以直接删除，孩子托管给父亲。

两个还是没办法给父亲，父亲养不了这么多孩子，但是可以找个人替代父亲养孩子。

当然，也不能随便找，找的人必须仍然维持搜索二叉树的性质，这是原则。

"你不能说搞得我都不是搜索二叉树了，那还玩个锤子"

必须比左边的大，比右边的小。所以在家族中找是最合适的。

找左子树的最大值结点，或者右子树的最小值结点。

首先要查找元素是否在二叉搜索树中，如果不存在，则返回。

如果存在，那么删除的结点可能分为下面四种情况：

a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左孩子结点也有右孩子结点

看起来有待删除节点有 4 种情况，但实际上 a 和 b，或 a 和 c 可以合并。

📌 因此，真正的删除过程如下：

情况B：删除该结点且使被删除结点的父结点指向被删除节点的左孩子结点 —— 直接删除。
情况C：删除该节点且使被删除结点的父节点指向被删除节点的右孩子结点 —— 直接删除。
情况D：在它的右子树中寻找中序下的第一个结点（值最小），用它的值填补到被删除结点中，再来处理该结点的删除问题 —— 替换法删除。

① 该结点无左孩子

如果要删除下面这颗二叉树的 10 节点和 4 节点：

我们还是定义一个 cur 变量，当 cur 找到 10 结点后，如果左侧为空情况如下：

若该结点为 root，直接让 root 等于它的右孩子结点。
对于删除 10 结点：若 cur==father->right，则令 parent->right = cur->right （如图所示）
对于删除 4 结点：若 cur==father->left，则令 parent->left=cur->right （如图所示）
最后删除 cur 结点

💬 代码演示：

if (cur->_left == nullptr) {/* 判断要删除的结点是否为根结点 */if (cur == _root) {_root = cur->_right;}else {if (cur == father->_right) {/* 如果 cur 比 father 大 */father->_right = cur->_right;}else {father->_left = cur->_right;}}delete cur;cur = nullptr;
}

② 该结点无右孩子

如果要删除 14 结点，删除逻辑和删除左孩子是类似的：

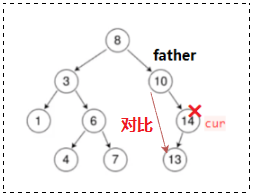
💬 代码演示：

else if (cur->_right == nullptr) {/* 判断是否为根结点 */if (cur == _root) {_root = cur->_left;}else {if (cur == father->_right) {/* cur 比父结点大 */father->_right = cur->_left;}else {father->_left = cur->_left;}}delete cur;cur = nullptr;
}

③ 该结点有左右两个孩子

如果删除的结点有左右两个孩子，我们就在它的右子树中寻找中序的第一个结点。

即与右子树的最小值进行替换，当然也可以选择左子树的最大值进行替换。

💭 例子：比如下面这颗子树，我们要删除 3 结点：

如果该结点有两个孩子，则采用如下替换法：

该结点和右子树的最小值或左子树的最大值进行值的替换，然后删除替换后的结点。

这里我们采用与右子树的最小值进行替换。

💬 代码演示：非递归版本的 Erase

bool Erase(const K& key) {Node* father = nullptr;Node* cur = _root;while (cur != nullptr) {if (cur->_key < key) {father = cur;cur = cur->_right;}else if (cur->_key > key){father = cur;cur = cur->_left;}else {/* 找到了！ 情况一：该节点没有左孩子   情况二：该节点没有右孩子 */if (cur->_left == nullptr) {/* 判断是否为根结点 */if (cur == _root) {_root = cur->_right;}else {if (cur == father->_right) {//cur 比 father大father->_right = cur->_right;}else {father->_left = cur->_right;}}delete cur;cur = nullptr;}else if (cur->_right == nullptr) {/* 判断是否为根结点 */if (cur == _root) {_root = cur->_left;}else {if (cur == father->_right) {/* 如果 cur 比父结点大 */father->_right = cur->_left;}else {father->_left = cur->_left;}}delete cur;cur = nullptr;}else {/* 有两个节点，替换 */Node* MinParNode = cur;Node* MinNode = cur->_right;while (MinNode->_left) {MinParNode = MinNode;MinNode = MinNode->_left;}swap(cur->_key, MinNode->_key);if(MinParNode->_left == MinNode) {MinParNode->_left = MinNode->_right;}else {MinParNode->_right = MinNode->_right;}delete MinNode;MinNode = nullptr;}return true;}}return false;
}

💡 解读：找到 3 结点中右子树的最小结点，替换它们的值。定义 MinParNode 为 cur，MinNode 为 cur 的右节点。首先让 MinNode 指向 3 的右孩子（1），然后一直向左边找知道找到 nullptr 为止，此时 MinNode 指向的就是最小的结点了，此时让 3 与 MinNode 的值交换即可。

交换后，删除 3 就变成了删除 MinNode，我们需要弄清 MinNode 和 MinParNode 的指向关系：

如果 MinParNode 的左孩子是 MinNode，则让 MinParNode 的左指向 MinNode 的右。
如果 MinParNode 的右孩子是 MinNode，则让 MinParNode 的右指向 MinNode 的右。（这里让 MinParNode 指向 MinNode 的右的原因是 MinNode 已是最小结点，不可能有左孩子了）

Ⅲ. 搜索二叉树的应用

0x00 K 模型

$K$ 模型，即只有 key 作为关键码，结构中只需存储 key 即可，关键码就是需要搜索到的值。

💭 举个例子：对于单词 word，我们需要判断该单词是否拼写正确

以单词集合中的每个单词作为 key，构建一个搜索二叉树。
在二叉树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

0x01 KV 模型

$KV$ 模型，每一个关键码 key，都有与之对应的值 Value，即 <Key, Value> 的键值对。

这就像 Python 中的 dict 字典类型一样，key 和 value 对应。

这在生活中也是非常常见的，比如英汉词典就是英文与中文的对应关系，通过英文可以快读检索到对应的中文，英文单词也可以与其对应的中文构建出一种键值对：

<word, chinese>

再比如统计单词次数，统计成功后，给定的单词就课快速找到其出现的次数，单词与其出现的次数就构建出了一种键值对：

<word, count>

💬 代码演示：我们实现一个简单的英汉词典 dict，可以通过英文找到对应的中文。

具体实现方式如下：

<单词, 中文含义> 以键值对构造搜索二叉树，值得注意的是，搜索二叉树需要比较，键值对比较时只比较 Key。
查询英文单词时，只需给出英文单词，就可以快速检索到对应的 Key

namespace KV
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;//pair<K, V> _kv;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>struct BSTree{typedef BSTreeNode<K, V> Node;public:BSTree():_root(nullptr){}bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 找到，准备开始删除if (cur->_left == nullptr){if (parent == nullptr){_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr){if (parent == nullptr){_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}else{Node* minParent = cur;Node* min = cur->_right;while (min->_left){minParent = min;min = min->_left;}cur->_key = min->_key;cur->_value = min->_value;if (minParent->_left == min)minParent->_left = min->_right;elseminParent->_right = min->_right;delete min;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root;};void TestBSTree1(){// 字典KV模型BSTree<string, string> dict;dict.Insert("sort", "排序");dict.Insert("left", "左边");dict.Insert("right", "右边");dict.Insert("map", "地图、映射");//...string str;while (cin>>str){BSTreeNode<string, string>* ret = dict.Find(str);if (ret){cout << "对应中文解释：" << ret->_value << endl;}else{cout << "无此单词" << endl;}}}void TestBSTree2(){// 统计水果出现次数string arr[] = { "苹果", "西瓜","草莓", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };BSTree<string, int> countTree;for (auto& str : arr){//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret != nullptr){ret->_value++;}else{countTree.Insert(str, 1);}}countTree.InOrder();}
}

📌 [ 笔者 ]   王亦优
📃 [ 更新 ]   2023.4.8
❌ [ 勘误 ]   /* 暂无 */
📜 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，本人也很想知道这些错误，恳望读者批评指正！

📜 参考资料

C++reference[EB/OL]. []. http://www.cplusplus.com/reference/.

Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. .

百度百科[EB/OL]. []. https://baike.baidu.com/.

比特科技. C++[EB/OL]. 2021[2021.8.31].

【C++要笑着学】搜索二叉树 (SBTree) | K 模型 | KV 模型

Ⅰ. 搜索二叉树（SearchBinaryTree）

0x00 搜索二叉树的概念

0x01 搜索二叉树的优势

0x02 二叉搜索树的时间复杂度：O(N)

0x03 搜索二叉树的改良方案

Ⅱ. 搜索二叉树的实现

0x00 搜索二叉树的定义

0x01 搜索二叉树的插入

0x02 搜索二叉树的查找

0x03 搜索二叉树删除

Ⅲ. 搜索二叉树的应用

0x00 K 模型

0x01 KV 模型

相关问题

公告