力扣54和59题

54.顺时针打印矩阵

题目：

 思路：将矩阵分为若干层，首先打印最外层的元素，然后一直往里打印

对于每层，从左上方开始以顺时针的顺序遍历所有元素。假设当前层的左上角位于(top,left)，右下角位于 (bottom,right)，按照如下顺序遍历当前层的元素。
（1）从左到右遍历上侧元素，依次为(top,left) 到(top,right)；
（2）从上到下遍历右侧元素，依次为(top+1,right) 到 (bottom,right)；
如果 left<right 且top<bottom，则
（3）从右到左遍历下侧元素，依次为(bottom,right−1)到(bottom,left+1)；
（4）从下到上遍历左侧元素，依次为(bottom,left)到 (top+1,left)。
遍历完当前层的元素之后，将 left 和 top 分别增加 1，将right 和 bottom 分别减少 1，进入下一层继续遍历，直到遍历完所有元素为止。
 

 C++代码：

//按层模拟
class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {if (!matrix.size() || !matrix[0].size()) return {};vector<int> res;int rows = matrix.size();   //最外层行数int columns = matrix[0].size(); //最外层列数int top = 0, left = 0, bottom = rows - 1, right = columns - 1;  //左上角：[top, left] 右下角：[bottom, right]while (left <= right && top <= bottom) {//遍历top行：left --> rightfor (int column = left; column <= right; ++column) {res.push_back(matrix[top][column]);}//遍历right列：top+1 --> bottomfor (int row = top + 1; row <= bottom; ++row) {res.push_back(matrix[row][right]);}//判断是否已经到了最里层if (left < right && top < bottom) {//遍历bottom行：right-1 --> left+1for (int column = right - 1; column > left; --column) {res.push_back(matrix[bottom][column]);}//遍历left列：bottom --> top+1for (int row = bottom; row > top; --row) {res.push_back(matrix[row][left]);}}top++;left++;bottom--;right--;}return res;}
};

59.螺旋矩阵

题目描述：

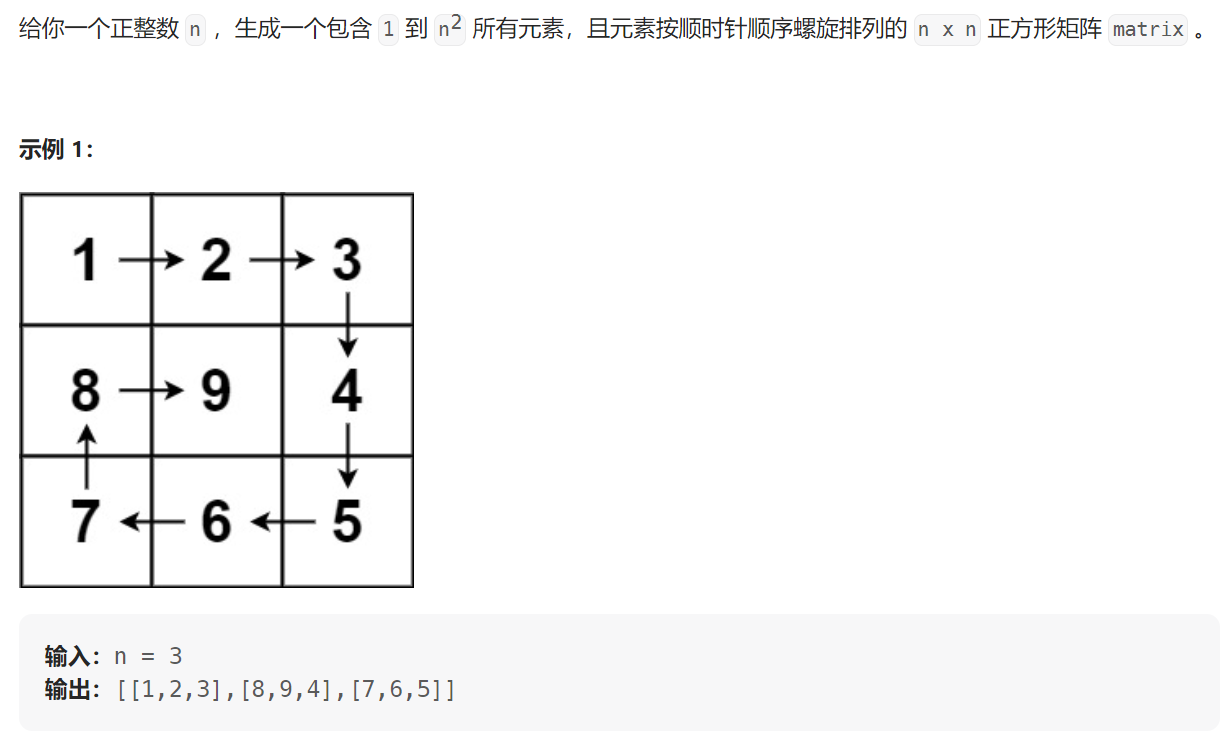
 思路：由于矩阵是n*n的，可以将矩阵分为n/2层来考虑，分层按照顺时针依次填充数字

#include <iostream>
using namespace std;
#include <vector>class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组int startx = 0, starty = 0; // 定义每循环一个圈的起始位置int loop = n / 2; // 每个圈循环几次，例如n为奇数3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理int mid = n / 2; // 矩阵中间的位置，例如：n为3， 中间的位置就是(1，1)，n为5，中间位置为(2, 2)int count = 1; // 用来给矩阵中每一个空格赋值int offset = 1; // 需要控制每一条边遍历的长度，每次循环右边界收缩一位int i, j;while (loop--) {// 下面开始的四个for就是模拟转了一圈// 模拟填充上行从左到右(左闭右开)for (j = starty; j < n - offset; j++) {res[startx][j] = count++;}// 模拟填充右列从上到下(左闭右开)for (i = startx; i < n - offset; i++) {res[i][j] = count++;}// 模拟填充下行从右到左(左闭右开)for (; j > starty; j--) {res[i][j] = count++;}// 模拟填充左列从下到上(左闭右开)for (; i > startx; i--) {res[i][j] = count++;}// 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)startx++;starty++;// offset 控制每一圈里每一条边遍历的长度offset += 1;}// 如果n为奇数的话，需要单独给矩阵最中间的位置赋值if (n % 2) {res[mid][mid] = count;}return res;}
};int main()
{   Solution solution1;int n = 5;vector<vector<int>> res = solution1.generateMatrix(n);for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){cout << res[i][j] << " ";}cout << endl;}}

螺旋矩阵本身不涉及算法，而是考察数据的一种遍历方式