1、bitXor

异或：不是同时为0和不是同时为1的情况进行按位与

/ bitXor - x^y using only ~ and &*   Example: bitXor(4, 5) = 1*   Legal ops: ~ &*   Max ops: 14*   Rating: 1*/int bitXor(int x, int y)
{return ~(~x & ~y) & ~(x & y);
}

2、tmin

int最小值就是符号位为1，其他为0

/ tmin - return minimum two's complement integer*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 4*   Rating: 1*/int tmin(void)
{return 0x01 << 31;
}

3、isTmax

我们考虑四位的最大值x=0111 然后x+1之后就会变成1000，我们对1000取非0111就会重新变回x值，已知自己与自己异或会得到0，也就是说我们可以用异或来判断等于!((~(x+1)^x)) 是否为1即可判断是否为最大值。这里有一个例外就是x=-1，由于-1=1111 他利用上面的式子判断也符合，故要特判-1，利用!!(x+1) 这个操作-1和最大值并不相同

/ isTmax - returns 1 if x is the maximum, two's complement number,*     and 0 otherwise*   Legal ops: ! ~ & ^ | +*   Max ops: 10*   Rating: 1*/int isTmax(int x)
{return !(~(x + 1) ^ x) & !!(x + 1);
}

4、allOddBits

A=1010， A是一个典型的奇数位都是1的数(起始位为第0位)，那只要一个四位的二进制数X & A = A就说明这个二进制符合条件，即只要判断x & 0xAAAAAAAA == 0xAAAAAAAA 就可以了。

由于不能直接定义0xAAAAAAAA ，我们需要一些位运算的小技巧

/ allOddBits - return 1 if all odd-numbered bits in word set to 1*   where bits are numbered from 0 (least significant) to 31 (most significant)*   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 12*   Rating: 2*/int allOddBits(int x)
{int mask = 0xAA;            // 0xAAmask = (mask << 8) + mask;  // 0xAAAAmask = (mask << 16) + mask; // 0xAAAAAAAAreturn !((x & mask) ^ mask);
}

5、negate

A + ~A = -1 和 A + (-A) =0 利用这两个式子我们可以得到 (-A) = ~A + 1

int值机器数为补码，补码取负为: 所有位取反然后加1即可

/ negate - return -x*   Example: negate(1) = -1.*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 5*   Rating: 2*/int negate(int x)
{return ~x + 1;
}

6、isAsciiDigit

我们可以看到“十”位必须是3， 并且只需要“个”位小于A即可，这里的小于运算 ，用了 a < b = a + (-b) < 0的性质，x & 0xF保存了x的后四位, 加上(-A)是否为负数来判断后四位的范围，判断负数是与0x1 << 31进行按位与运算，如果结果最高位为1则为负数

/ isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')*   Example: isAsciiDigit(0x35) = 1.*            isAsciiDigit(0x3a) = 0.*            isAsciiDigit(0x05) = 0.*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 15*   Rating: 3*/int isAsciiDigit(int x)
{int ah = !(x >> 4 ^ 0x3);int al = x & 0xF;int minus_a = ~0xA + 1;int flag = 0x1 << 31;return ah & !!((al + minus_a) & flag);
}

7、conditional

当x非0, 则!x为0, !!x为1, 令x = !!x，则此时~x+1为全1

若x为0, 则!!x为0, ~x+1还是为0

/ conditional - same as x ? y : z*   Example: conditional(2,4,5) = 4*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 16*   Rating: 3*/
// x > 0 return y else return zint conditional(int x, int y, int z)
{x = !!(x);x = ~x + 1;return (x & y) | ((~x) & z);
}

8、isLessOrEqual

注意：直接用x-y可能会爆int故不能通过这样简单的判断, 故进行分类讨论

• case 1代表x < 0, y > 0，
• case 2代表x > 0, y < 0。
• 在x y同号时(同大于0或同小于0时)，我们可以放心的进行x-y操作，这样确保不会因为溢出而导致结果的符号错误，因此这两种情况可以合并为一种情况, 即case 3。

显然case 1是符合条件的，case 2不符合条件但它却是统一讨论情况3的障碍，所以最终在返回条件中一定要有!case 2来将情况2排除掉，再与两种同号条件相与。

/ isLessOrEqual - if x <= y  then return 1, else return 0*   Example: isLessOrEqual(4,5) = 1.*   Legal ops: ! ~ & ^ | + << >>*   Max ops: 24*   Rating: 3*/
// 若x<=y则返回1, 否则返回0int isLessOrEqual(int x, int y)
{int sign_x = (x >> 31) & 0x1;int sign_y = (y >> 31) & 0x1;// case 1: x为-，y为+int case_1 = sign_x & (!sign_y);// case 2: x为+，y为-int case_2 = (!sign_x) & sign_y;// case 3: x与y同号int minus_y = (~y) + 1; // -yint sum = x + minus_y;  // x + (-y) = x - y// 判断sum是否 <= 0// 判断 = 0，若sum == 0, eq一定为1int eq = !sum;// 判断 < 0，若sum < 0，less一定为1int less = (sum >> 31) & 0x1;return case_1 | (!case_2 & (eq | less));
}

9、logicalNeg

非零数x，-x | x一定可以保证符号位为1。而对于0，这样的结论是不成立的，这就找到了能够完全区分0值和非0值的一个清晰的边界。

/ logicalNeg - implement the ! operator, using all of*              the legal operators except !*   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1*   Legal ops: ~ & ^ | + << >>*   Max ops: 12*   Rating: 4*/int logicalNeg(int x)
{int res = ((x | (~x + 1)) >> 31); // //除了0以外，其他的数都可以让res取到全1return res + 1;                   // res=0xffffffff, 因为int右移符号扩展 x|（～x+1）在x非0情况下必定是负数
}

10、howManyBits

        为了便于处理，将负数转换成对应的反码，再求解最高位1所在的位置

        正数的话直接求解最高位1所在的位置即可。最终结果为，最高位1所在的位置 + 1(符号位)，比如，0111 -> 3 + 1(符号位)

        注：这里最高位所在的位置表示该位置是第几位(从1开始计算), 第一位、第二位、......

求解最高位1所在位置使用二分法：

        如果x的高16位不为0，将x右移16位，然后用b16记录一下最高位1后面至少有16个数，

x右移16位之后，再接着二分，右移8位，

        如果x的高8位不为0，将x右移8位，然后用b8记录一下最高位1后面至少有8个数

        以此类推，最后将最高位1后面的数(包括自己)都加起来，即b16 + b8 + b4 + b2 + b1 + b0，再加一个符号位，即为最终答案b16 + b8 + b4 + b2 + b1 + b0 + 1

/* howManyBits - return the minimum number of bits required to represent x in*             two's complement*  Examples: howManyBits(12) = 5*            howManyBits(298) = 10*            howManyBits(-5) = 4*            howManyBits(0)  = 1*            howManyBits(-1) = 1*            howManyBits(0x80000000) = 32*  Legal ops: ! ~ & ^ | + << >>*  Max ops: 90*  Rating: 4*/int howManyBits(int x)
{int b16, b8, b4, b2, b1, b0;int sign = x >> 31;x = (sign & ~x) | (~sign & x);b16 = !!(x >> 16) << 4; // 10000, 16x = x >> b16;b8 = !!(x >> 8) << 3; // 1000, 8x = x >> b8;b4 = !!(x >> 4) << 2; // 100, 4x = x >> b4;b2 = !!(x >> 2) << 1; // 10, 2x = x >> b2;b1 = !!(x >> 1); // 1, 1x = x >> b1;b0 = x;return b16 + b8 + b4 + b2 + b1 + b0 + 1;
}

浮点数部分最重要的是理解下面这张图（太重要了！！！，不然根本没思路解题）

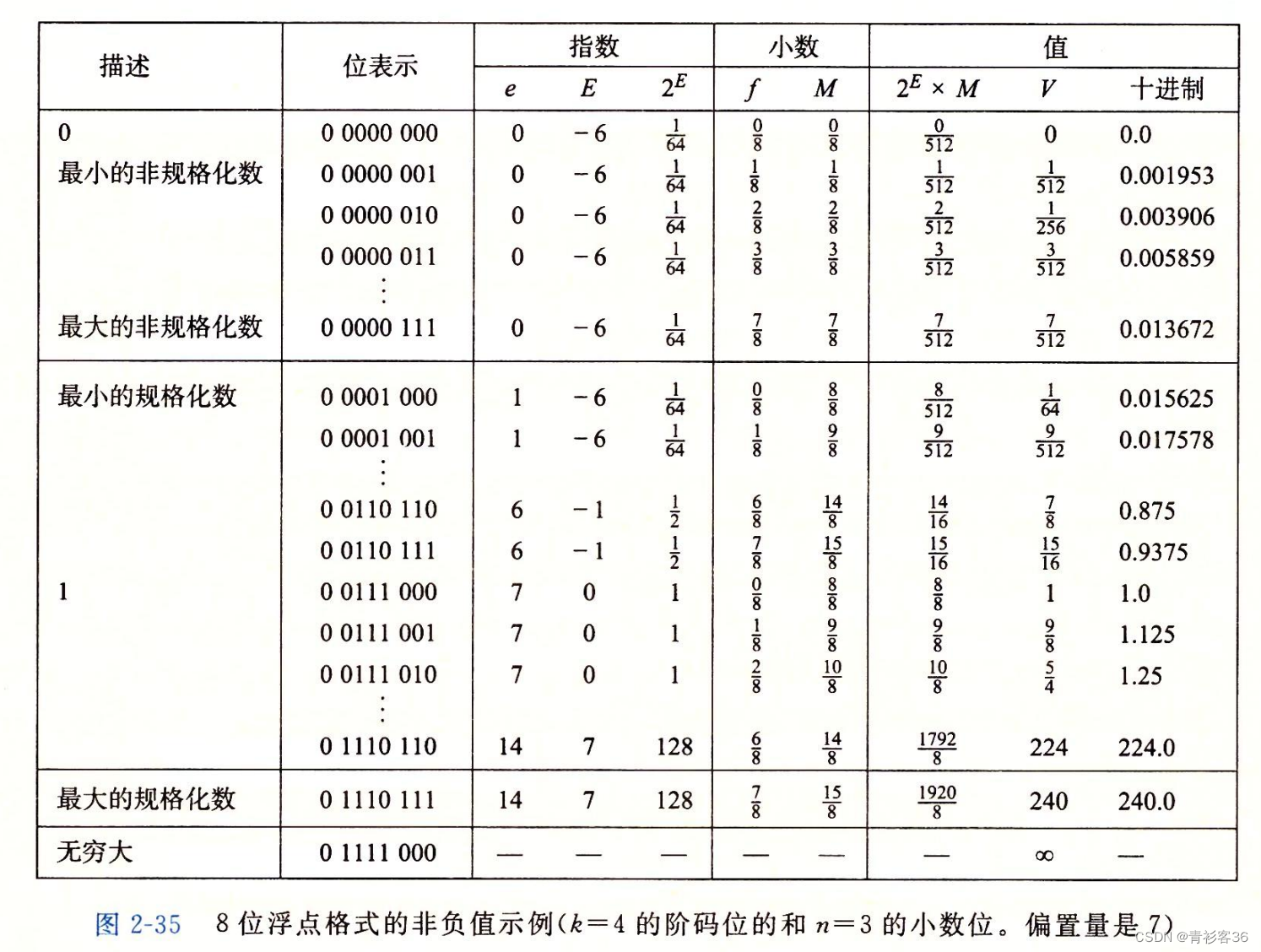
11、floatScale2

// float
/ floatScale2 - Return bit-level equivalent of expression 2*f for*   floating point argument f.*   Both the argument and result are passed as unsigned int's, but*   they are to be interpreted as the bit-level representation of*   single-precision floating point values.*   When argument is NaN, return argument*   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while*   Max ops: 30*   Rating: 4*/
unsigned floatScale2(unsigned uf)
{unsigned s = (uf >> 31) & (0x1);unsigned exp = (uf >> 23) & (0xff);unsigned frac = (uf & 0x7fffff);// 0if (exp == 0 && frac == 0)return uf;// 无穷大/NANif (exp == 0xff)return uf;// 非规格化if (exp == 0){// E = exp - 127 = -127// fracfrac <<= 1; // *2return (s << 31) | frac;}// 规格化exp++; // E = exp - 127return (s << 31) | (exp << 23) | (frac);
}

12、floatFloat2Int

/ floatFloat2Int - Return bit-level equivalent of expression (int) f*   for floating point argument f.*   Argument is passed as unsigned int, but*   it is to be interpreted as the bit-level representation of a*   single-precision floating point value.*   Anything out of range (including NaN and infinity) should return*   0x80000000u.*   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while*   Max ops: 30*   Rating: 4*/
int floatFloat2Int(unsigned uf)
{unsigned s = (uf >> 31) & (0x1);unsigned exp = (uf >> 23) & (0xff);unsigned frac = (uf & 0x7fffff);// 0if (exp == 0 && frac == 0)return 0;// 无限大/NANif (exp == 0xff)return 0x80000000u;// 非规格化if (exp == 0){// M 0.1111... < 1// E = 1 - 127 = -126return 0;}// 规格化// M 1.xXXXXint E = exp - 127;frac = frac | (1 << 23);if (E > 31) // 爆intreturn 0x80000000u;else if (E < 0){return 0;}// M * 2^Eif (E > 23){frac <<= (E - 23);}else{frac >>= (23 - E);}if (s)return ~frac + 1;return frac;
}

13、floatPower2

/ floatPower2 - Return bit-level equivalent of the expression 2.0^x*   (2.0 raised to the power x) for any 32-bit integer x.   The unsigned value that is returned should have the identical bit*   representation as the single-precision floating-point number 2.0^x.*   If the result is too small to be represented as a denorm, return*   0. If too large, return +INF.   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while*   Max ops: 30*   Rating: 4*/
/*非规格化浮点数的范围：2^-149 - 2^-126规格化浮点数的范围：  2^-126 - 2^127
*/
unsigned floatPower2(int x)
{if (x < -149)return 0;else if (x < -126){// E = x// E = 1 - 127 = -126int shift = 23 + (x + 126);return 1 << shift;}else if (x <= 127){// x = exp - biasint exp = x + 127;return exp << 23;}else{return (0xff) << 23;}
}

测试结果 

写在最后：笔者仰慕CSAAPLab已久，今日终于可以动手做做了，不得不说，Lab的质量确实高，做完本次实验，感觉自己对计算机中信息位的表示与处理的理解更深了一步，由于写博客的时间比较仓促，博客中出现的问题还请各位大神在评论区批评指正，谢谢大家！