✨博文作者 wangzirui32
💖 喜欢的可以 点赞 收藏 关注哦~~
👉本文首发于CSDN，未经许可禁止转载

Hello，大家好，我是wangzirui32，今天我们来学习如何用Python无限逼近求积分，开始学习吧！

1. 引入

某店的wifi密码如上图，要想连接该店的wifi，应该如何求出密码呢？

2. 原理分析

笔者先以正弦函数的图像进行分析，如下图：（稍有瑕疵，望理解）

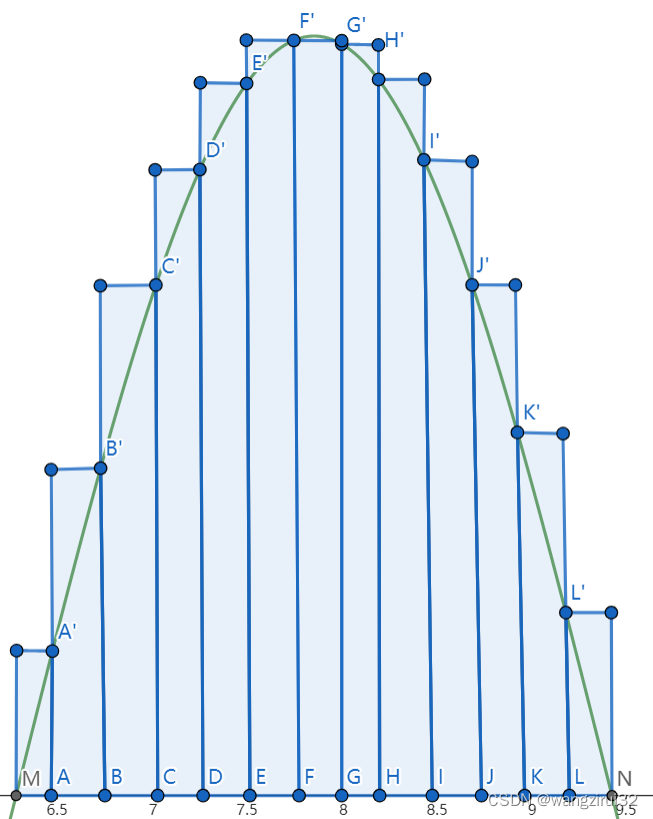
如图，绿色的线为函数曲线，M为待求积分起点，N为待求积分终点。x轴被等分为n份（即A,B,C,D,E,F,G,H,I,J,K,L等点），其中每个点都在函数曲线上同x值的点存在对应点（即A',B',C',D',E',F',G',H',I',J',K',L'等点），分别连接对应点，将对应点的连线作为长，x轴上相邻两点的连线为宽，构造长方形。
可以看到，所有长方形的面积和与函数曲线与x轴围成的区域的面积相近。当n越大，这两个数值就越接近，越逼近真实值。
那么如何求所有长方形的面积和呢？
可从图中看出，每个长方形的宽是固定的，为1/n（分成n份），长就是x对应的y值，即f(x)，所以面积和$S$为：
S=1nf(x1)+1nf(x2)+1nf(x3)+...S = \\frac{1}{n}f(x_1) + \\frac{1}{n}f(x_2) +\\frac{1}{n}f(x_3) + ... S=n1​f(x1​)+n1​f(x2​)+n1​f(x3​)+...
运用乘法分配律，得：
S=1n[f(x1)+f(x2)+f(x3)+...]S = \\frac{1}{n}[f(x_1) + f(x_2) + f(x_3) + ... ] S=n1​[f(x1​)+f(x2​)+f(x3​)+...]
其中xm−xm−1=Δx=1nx_m - x_{m-1} = \\Delta x = \\frac{1}{n}xm​−xm−1​=Δx=n1​（即相邻点x的差为固定值1n\\frac{1}{n}n1​）.

3. 代码

有了如上分析，可快速写出计算代码：

from math import cosdef f(x):                           # wifi密码的积分函数return ((x3)*cos(x/2)+0.5)*((4-x2)0.5)def calculus():n = 1*108                     # n取一个较大值max_limit, min_limit = 2, -2    # 积分的上下限weight = 1/n                    # 长方形的宽（同时是delta x）x = min_limit                   # 从积分下限开始迭代result = 0while x < max_limit:result += f(x)*weight       # 累加面积x += weight                 # 计算下一个x值return resultprint(calculus())

运行结果如下：

3.141592656855682

竟然和圆周率的值相近，前8位就是14159265，即wifi密码.

4. 优化

当n较大时，计算速度会大幅度减慢，可以使用Numba（见笔者文章）进行提速：

from math import cos
from numba import njit@njit
def f(x):return ((x3)*cos(x/2)+0.5)*((4-x2)0.5)@njit
def calculus():n = 1*1010max_limit, min_limit = 2, -2weight = 1/nx = min_limitresult = 0while x < max_limit:result += f(x)*weightx += weightreturn resultprint(calculus())

🎉🎉🎉 好了，今天的课程就到这里，我是wangzirui32，喜欢的可以点个收藏和关注，我们下次再见！