反向传播推导+numpy实现

文章列表

反向传播推导+numpy实现

很久没有看深度学习了，忘了好多东西。本来想着推导一下，后来发现自己不会了。
再看看以前写的代码，又避开了最终的东西，于是决定重新推导一下。

数据的说明

首先，我们要做一个回归的任务，我们使用numpy随机的生成一些数据
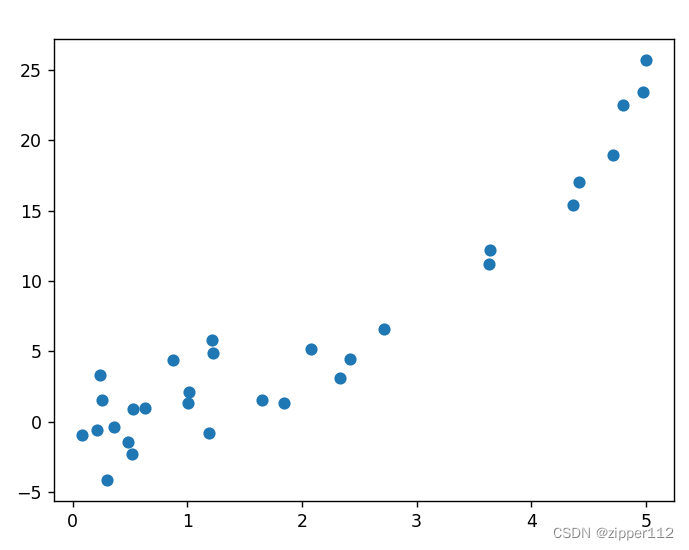
反向传播推导+numpy实现
生成的代码如下，可以看到这一个二次函数，但是我们加入了一些随机的噪声使其更像真实的数据。

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(333)
data = np.random.random(size=(1, 30)) * 5 # 随机生成30个点
data = np.sort(data, axis=1)
y = (data  2).T + np.random.randn(30, 1) * 2 # 加入随机噪声
plt.scatter(data, y.T)
plt.show()

然后我们对数据进行升维，使得我们的网络能够捕捉到更多的特征。

np.random.seed(333)
data = np.random.random(size=(1, 30)) * 5
data = np.sort(data, axis=1)
y = (data  2).T + np.random.randn(30, 1) * 2
t_data = np.vstack([ # 升维度data,data  2
])

所以我们现在每个数据有两个特征，一个是原本的x，一个是 $x^2$ 。我们的数据集的形状是 $2 \times 30$ 其中30是样本数，2是特征数。每一列是一个样本。

前向传播

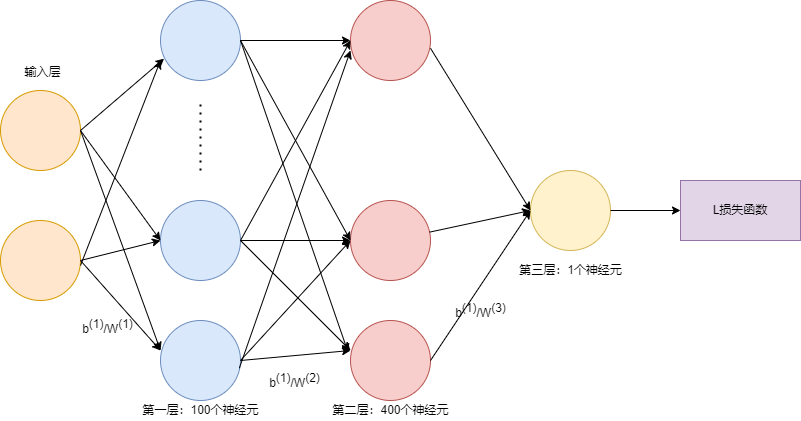
我们首先来设定一下各个参数，如下写的参数都是其形状。

$w^{(1)}=(100, 4), b^{(1)}=(100, 1)$
$w^{(2)}=(400, 100), b^{(2)}=(400, 1)$
$w^{(3)}=(1, 400), b^{(3)}=(1, 1)$

如上图所示，不算输入层，这是一个三层的网络，每一层左侧的连线就是权重参数和偏置参数

前向传播计算过程(这里我们只算单个样本的)：

$z^{(1)}=b^{(1)}+w^{(1)}x$

$a^{(1)}=sigmoid(z^{(1)})$

$z^{(2)}=b^{(2)}+w^{(2)}a^{(1)}$

$a^{(2)}=sigmoid(z^{(2)})$

$z^{(3)}=b^{(3)}+w^{(3)}a^{(2)}$

$L = (z^{(3)} - y)^2$
由于这里我们只算单个样本的误差，所以我们最后的损失函数计算不需要除以n

反向传播

delta的计算

首先，我们需要引入一个中间变量，叫做 $δj(l)\\delta^{(l)}_j$ ，其定义为 $δj(l)=∂L∂zj(l)\\delta^{(l)}_j=\\frac{\\partial L}{\\partial z^{(l)}_j}$ 这是一个关键的中间变量。

第三层的 $δ\\delta$ 计算

由于这一层只有一个z，所以我们可以直接得出 $δj(3)=∂L∂zj(3)=2(zj(3)−y)\\delta ^{(3)}_j = \\frac{\\partial L}{\\partial z^{(3)}_j}=2(z^{(3)}_j - y)$
第二层的 $δ\\delta$ 计算

我们希望递归的去计算 $δ\\delta$ 所以，我们必须要用 $δ(3)\\delta^{(3)}$ 的计算信息来推出 $δ(2)\\delta^{(2)}$ 的，也就是我们要化成如下这种形式：
$δj(2)=∂L∂zj(2)=∂L∂z(3)∂z(3)∂zj(2)\\delta ^{(2)}_j = \\frac{\\partial L}{\\partial z^{(2)}_j}=\\frac{\\partial L}{\\partial z^{(3)}}\\frac{\\partial z^{(3)}}{\\partial z^{(2)}_j}$
注意，这个式子并不是一个精确地式子，但是可以看出，通过这种链式法则的拆解，我们得到的第一项中含有 $δ(3)\\delta^{(3)}$ 。
对于 $zi(2)z^{(2)}_i$ 它的产生，都需要经过 $zj(3)z^{(3)}_j$ 的计算，所以根据链式求导法则我们有
$δj(2)=∂L∂zj(2)=∑k=11∂L∂zk(3)∂zk(3)∂zj(2)\\delta ^{(2)}_j = \\frac{\\partial L}{\\partial z^{(2)}_j}=\\sum\\limits_{k=1}^1\\frac{\\partial L}{\\partial z^{(3)}_k}\\frac{\\partial z^{(3)}_k}{\\partial z^{(2)}_j}$ .
形象的来说，就是我们利用链式求导法则计算时，我们把 $∂L∂zj(2)\\frac{\\partial L}{\\partial z^{(2)}_j}$ 拆成 $∂L∂z(3)∂z(3)∂zj(2)\\frac{\\partial L}{\\partial z^{(3)}}\\frac{\\partial z^{(3)}}{\\partial z^{(2)}_j}$ 时中间有若干个中间变量 $zk(3)z^{(3)}_k$ , 所以我们对于每一个中间变量都需要求出它的分量。
接下来我们求解 $∂zk(3)∂zj(2)\\frac{\\partial z^{(3)}_k}{\\partial z^{(2)}_j}$ ，我们写出 $z^{(3)}$ 的表达式：
$zk(3)=∑iwk,i(3)σ(zi(2))+bk(3)z^{(3)}_k=\\sum\\limits_i w^{(3)}_{k,i}\\sigma(z^{(2)}_i) + b^{(3)}_k$
于是我们得到 $∂zk(3)∂zj(2)=wk,jσ′(zj(2))\\frac{\\partial z^{(3)}_k}{\\partial z^{(2)}_j}=w_{k,j}\\sigma'(z_j^{(2)})$ , 于是我们得到最终的计算式
$δj(2)=∂L∂zj(2)=∑k=11δk(3)wk,j(3)σ′(zj(2))\\delta ^{(2)}_j = \\frac{\\partial L}{\\partial z^{(2)}_j}=\\sum\\limits_{k=1}^1\\delta^{(3)}_kw^{(3)}_{k,j}\\sigma'(z_j^{(2)})$ .
于是我们得到 $δ(2)=(w(3))Tδ(3)⨂σ′(z(2))\\delta^{(2)}=(w^{(3)})^T\\delta^{(3)}\\bigotimes \\sigma'(z^{(2)})$
第一层的计算

同样的思路，我们的计算方式和第二层一模一样
$δj(1)=∂L∂zj(1)=∑k=1400δk(2)wk,j(2)σ′(zj(1))\\delta ^{(1)}_j = \\frac{\\partial L}{\\partial z^{(1)}_j}=\\sum\\limits_{k=1}^{400}\\delta^{(2)}_kw^{(2)}_{k,j}\\sigma'(z_j^{(1)})$ .
我们写成向量形式
$[δ1(1)δ2(1)...δ100(1)]=[δ1(2)w1,1(2)+δ2(2)w2,1(2)+...+δ400(2)w400,1(2)δ1(2)w1,2(2)+δ2(2)w2,2(2)+...+δ400(2)w400,2(2)...δ1(2)w1,100(2)+δ2(2)w2,100(2)+...+δ400(2)w400,100(2)]⨂[σ′(z1(1))σ′(z2(1))...σ′(z100(1))]\\begin{bmatrix} \\delta^{(1)}_1 \\\\ \\delta^{(1)}_2 \\\\ ...\\\\ \\delta^{(1)}_{100} \\end{bmatrix} = \\begin{bmatrix} \\delta^{(2)}_1w^{(2)}_{1,1}+\\delta^{(2)}_2w^{(2)}_{2,1}+...+\\delta^{(2)}_{400}w^{(2)}_{400,1}\\\\ \\delta^{(2)}_1w^{(2)}_{1,2}+\\delta^{(2)}_2w^{(2)}_{2,2}+...+\\delta^{(2)}_{400}w^{(2)}_{400,2}\\\\ ...\\\\ \\delta^{(2)}_1w^{(2)}_{1,100}+\\delta^{(2)}_2w^{(2)}_{2,100}+...+\\delta^{(2)}_{400}w^{(2)}_{400,100} \\end{bmatrix} \\bigotimes \\begin{bmatrix} \\sigma'(z^{(1)}_1)\\\\ \\sigma'(z^{(1)}_2)\\\\ ...\\\\ \\sigma'(z^{(1)}_{100}) \\end{bmatrix}$
可以得到 $δ(1)=(w(2))Tδ(2)⨂σ′(z(1))\\delta^{(1)}=(w^{(2)})^T\\delta^{(2)}\\bigotimes \\sigma'(z^{(1)})$

b和w的偏导计算

$w$ 和 $b$ 的梯度计算

有了 $δ\\delta$ 之后，想要计算这两个，可以说是很简单了。
由于 $∂L∂bi=δi∂zi∂bi\\frac{\\partial L}{\\partial b_i}=\\delta_i \\frac{\\partial z_i}{\\partial b_i}$ 根据z和b的关系，所以 $∂zi∂bi=1\\frac{\\partial z_i}{\\partial b_i}=1$ 最终我们得到了梯度
$∂L∂bi=δi\\frac{\\partial L}{\\partial b_i}=\\delta_i$
接下来我们计算 $w$
$∂L∂wi,j=δi∂zi∂wi,j=δiaj\\frac{\\partial L}{\\partial w_{i,j}}=\\delta_i \\frac{\\partial z_i}{\\partial w_{i,j}}=\\delta_i a_j$ 然后我们改写成矩阵形式
$∂L∂w(l)=δ(l)(a(l−1))T\\frac{\\partial L}{\\partial w^{(l)}}=\\delta^{(l)}(a^{(l-1)})^T$
总结一下
$∂L∂b(l)=δ(l)∂L∂w(l)=δ(l)(a(l−1))T\\frac{\\partial L}{\\partial b^{(l)}}=\\delta^{(l)}\\\\\\frac{\\partial L}{\\partial w^{(l)}}=\\delta^{(l)}(a^{(l-1)})^T$

代码实现

class FFCN:def __init__(self) -> None:self.w1 = np.random.randn(100, 2)self.b1 = np.random.randn(100).reshape(-1, 1)self.w2 = np.random.randn(400, 100)self.b2 = np.random.randn(400).reshape(-1, 1)self.w3 = np.random.randn(1, 400)self.b3 = np.random.randn(1).reshape(-1, 1)def forward(self, x: np.ndarray):"""x: (4, 1)"""self.z1 = self.w1.dot(x) + self.b1self.a1 = self.__sigmoid(self.z1)self.z2 = self.w2.dot(self.a1) + self.b2self.a2 = self.__sigmoid(self.z2)self.z3 = self.w3.dot(self.a2) + self.b3return self.z3def predict(self, x: np.ndarray): # 用于预测多组的结果return np.array([self.forward(x[:, i].reshape(-1, 1))[0][0] for i in range(x.shape[1])])def backpp(self, data: np.ndarray, target: np.ndarray, lr:float=0.002, iter:int=200):"""lr: 学习率iter: 迭代次数"""for _ in range(iter):loss = 0for i in range(data.shape[1]):x = data[:, i].reshape(-1, 1)y = target[i]loss += (self.forward(x) - y)  2self.delta3 = 2 * (self.z3 - y)self.delta2 = self.w3.T.dot(self.delta3) * self.__dsigmoid(self.z2)self.delta1 = self.w2.T.dot(self.delta2) * self.__dsigmoid(self.z1)self.dw1 = self.delta1.dot(x.reshape(1,-1))self.dw2 = self.delta2.dot(self.a1.T)self.dw3 = self.delta3.dot(self.a2.T)self.__step(lr)print("loss of", _, ":", loss[0][0])loss = 0def __sigmoid(self, x):# 激活函数return 1 / (1 + np.exp(-x))def __dsigmoid(self, x):return np.exp(x) / ((1 + np.exp(x))  2)def __step(self, lr: float): # 更新参数权重self.w1 -= self.dw1 * lrself.w2 -= self.dw2 * lrself.w3 -= self.dw3 * lrself.b1 -= self.delta1 * lrself.b2 -= self.delta2 * lrself.b3 -= self.delta3 * lr

效果：
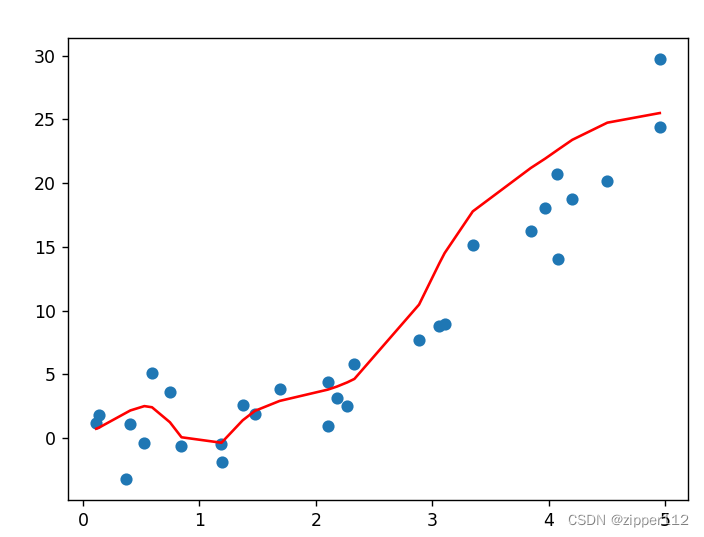
反向传播推导+numpy实现
完整代码：

import numpy as np
import matplotlib.pyplot as plt"""
造一个三层的神经网络"""class FFCN:def __init__(self) -> None:self.w1 = np.random.randn(100, 2)self.b1 = np.random.randn(100).reshape(-1, 1)self.w2 = np.random.randn(400, 100)self.b2 = np.random.randn(400).reshape(-1, 1)self.w3 = np.random.randn(1, 400)self.b3 = np.random.randn(1).reshape(-1, 1)def forward(self, x: np.ndarray):"""x: (4, 1)"""self.z1 = self.w1.dot(x) + self.b1self.a1 = self.__sigmoid(self.z1)self.z2 = self.w2.dot(self.a1) + self.b2self.a2 = self.__sigmoid(self.z2)self.z3 = self.w3.dot(self.a2) + self.b3return self.z3def predict(self, x: np.ndarray):return np.array([self.forward(x[:, i].reshape(-1, 1))[0][0] for i in range(x.shape[1])])def backpp(self, data: np.ndarray, target: np.ndarray, lr:float=0.002, iter:int=200):for _ in range(iter):loss = 0for i in range(data.shape[1]):x = data[:, i].reshape(-1, 1)y = target[i]loss += (self.forward(x) - y)  2self.delat3 = 2 * (self.z3 - y)self.delat2 = self.w3.T.dot(self.delat3) * self.__dsigmoid(self.z2)self.delta1 = self.w2.T.dot(self.delat2) * self.__dsigmoid(self.z1)self.dw1 = self.delta1.dot(x.reshape(1,-1))self.dw2 = self.delat2.dot(self.a1.T)self.dw3 = self.delat3.dot(self.a2.T)self.__step(lr)print(_, ":", loss[0][0])loss = 0def __sigmoid(self, x):return 1 / (1 + np.exp(-x))def __dsigmoid(self, x):return np.exp(x) / ((1 + np.exp(x))  2)def __step(self, lr: float):self.w1 -= self.dw1 * lrself.w2 -= self.dw2 * lrself.w3 -= self.dw3 * lrself.b1 -= self.delta1 * lrself.b2 -= self.delat2 * lrself.b3 -= self.delat3 * lrmodel = FFCN()np.random.seed(111)
data = np.random.random(size=(1, 30)) * 5
data = np.sort(data, axis=1)
y = (data  2).T + np.random.randn(30, 1) * 2
t_data = np.vstack([data,data  2
])
model.backpp(t_data, y)
plt.scatter(data, y.T)
plt.plot(data.squeeze(0), model.predict(t_data), color='r')
plt.show()

反向传播推导+numpy实现

数据的说明

前向传播

反向传播

delta的计算

b和w的偏导计算

$w$ 和 $b$ 的梯度计算

代码实现

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

标签

反向传播推导+numpy实现

数据的说明

前向传播

反向传播

delta的计算

b和w的偏导计算

www和bbb的梯度计算

代码实现

相关问题

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

标签

$w$ 和 $b$ 的梯度计算