试题F：全排列的价值——蓝桥杯第十三届省赛Java 大学A组

​

试题F：全排列的价值

其实就是将1到N数进行全排列，然后每个数前面有多少个数小于当前数当前数就计算为多少分。
如某排列为(1,2,3,4)那么她的价值数组为(0,1,2,3)，因为第一位前面没有小于1的，第二位有一个数小于2……。
这道题很明显的动态规划问题，当我们计算出X-1个数据的全排列价值的时候，计算X个数据的全排列则为：
$$f(x)=xf(x-1)+(x-1)\ast x!/2$$

推理过程以2到3为例：
只有两种，并且价值为(0, 1)+(0, 0)=1

当从2扩展到3时，插入位置可以有三个地方：
每个队列的前面，中间，后面。

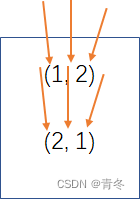
此时还需要注意一个问题，如果插入一个最大的数，那么数组的其他位置的价值不变，如(1,2)到(1,3,2)这个中间插入，1和2这两个数价值并未发生变化，因为价值是前面小于该位置的数。
所以(1,2)到(1,3,2)等于V(1,2) 增加添加到第二个位置的3的价值。而3是最大的数，所以只需要知道3添加到哪里了就能了解当前扩展了多少价值，在这里增加了1。

所以从2扩展到3，排列方式可以通过上图很明显的知道排列种类增加了3倍，而每个位置的3的价值也可以计算出来:

所以扩展的倍率为x，扩展的价值x*f(x-1)，每个x在其位置的价值为x(x-1)/2*(x-1)!（首项加末项乘以项数除以2 * 上一级排列方式）。
由于有除数运算，整理后：
$$f(x)=xf(x-1)+(x-1)\ast x!/2$$

Java代码

package com.maggot.maggotscheduler.bootstrap.utils.lanqiaobei13;
import java.math.BigInteger;
/* @author huangyichun*/
public class F全排列的价值 {/* 标准的动态规划题目* 根据上一次的结果，进行指数扩展* 方程为: xf(x-1)+(x-1)x!/2*/public static void main(String[] args) {
//        System.out.println(getValue(2).remainder(BigInteger.valueOf(998244353)));
//        System.out.println(getValue(3).remainder(BigInteger.valueOf(998244353)));
//        System.out.println(getValue(4).remainder(BigInteger.valueOf(998244353)));System.out.println(getValue(2022).remainder(BigInteger.valueOf(998244353)));//        System.out.println(dp(2).remainder(BigInteger.valueOf(998244353)));
//        System.out.println(dp(3).remainder(BigInteger.valueOf(998244353)));
//        System.out.println(dp(4).remainder(BigInteger.valueOf(998244353)));
//        System.out.println(dp(5).remainder(BigInteger.valueOf(998244353)));
//        System.out.println(dp(6).remainder(BigInteger.valueOf(998244353)));
//        System.out.println(dp(7).remainder(BigInteger.valueOf(998244353)));System.out.println(dp(2022).remainder(BigInteger.valueOf(998244353)));}public static BigInteger getValue(int number) {BigInteger nowValue = BigInteger.ZERO;for (int i = 2; i <= number; i++) {nowValue = BigInteger.valueOf(i).multiply(nowValue).add(BigInteger.valueOf(i - 1).multiply(factorial(i)).divide(BigInteger.valueOf(2)));}return nowValue;}public static BigInteger dp(int i) {if (i == 2) {return BigInteger.ONE;}BigInteger nowValue = BigInteger.valueOf(i).multiply(dp(i - 1)).add(BigInteger.valueOf(i - 1).multiply(factorial(i)).divide(BigInteger.valueOf(2)));return  nowValue;}public static BigInteger factorial(int number) {if (number < 2) {return BigInteger.ZERO;}BigInteger b = BigInteger.ONE;for (int i = 1; i <= number; i++) {b = b.multiply(BigInteger.valueOf(i));}return b;}
}

​