论文赏析——约翰·科斯塔斯:线性系统编码

© 1952 J. P. Costas
© 2023 Conmajia
作者简介 约翰·彼得·科斯塔斯(1923-2008),美国电气工程师,曾发明科斯塔斯环和科斯塔斯数组。科斯塔斯参加过第二次世界大战,并在战后进入麻省理工学院攻读博士学位,后于通用电气公司工作直至退休。1965 年,科斯塔斯当选为 IEEE 会士(fellow)。
世界线收束 科斯塔斯的这篇《线性系统编码》论文发表于 1952 年,刊印在 IRE1 1952 年 9 月会议报告(Proceedings of the I.R.E.)第 1101 页的下半页。有趣的是,本文前面一篇文章——也就是结束于第 1101 页上半页的那篇——题为《一种构建最小冗余码的方法》,作者是戴维·艾伯特·赫夫曼:不错,正是那篇诞生了信息科学中鼎鼎大名的 Huffman2 算法的文章。
考古 本文很多内容,例如脉冲响应等,在如今学过《信号与系统》课程的工程人员看来都已经属于常识。然而在撰写本文的 1950 年代,这些“常识”还需要在行文中专门指出其定义和参考文献。
以下为论文。
摘要 本文考虑了在噪声信道上的消息传输。设计了两个线性网络:一个在传输前处理信息;第二个用于在接收端对处理后的消息加上信道噪声进行过滤。本文给出的方法可以在给定的允许平均信号功率下,通过适当的网络设计,使传输电路的实际输出与期望输出之间的均方误差最小化。本文还给出并讨论了数值算例的结果。
线性系统编码
文章目录
- 线性系统编码
-
- I. 简介
- II. 传输问题
- III. 长延迟的解
- IV. 结果讨论
- 参考文献
- 致谢
I. 简介
笔者在即将发表的文献 4 中讨论了由维纳首创(文献 1、2)并由李(文献 3)发展的统计方法之于滤波器设计的重要性这一概念。简而言之,对于如图 1 所示输入为给定消息和噪声之和的系统,我们希望找到一种滤波器的特性,以提供最佳的性能。所谓“最佳”,我们指的是使得实际输出 fo(t)f_o(t)fo(t) 和期望输出 fd(t)f_d(t)fd(t) 之间的均方误差最小化这样的滤波器。也就是说,若以 ε\\varepsilonε 表示滤波的均方误差,即
ε=limT→∞12T∫−TT[fo(t)−fd(t)]2dt.(1)\\varepsilon=\\lim_{T\\to\\infty}\\frac{1}{2T}\\int_{-T}^{T}\\left[f_o(t)-f_d(t)\\right]^2\\mathrm{d}t.\\tag{1} ε=T→∞lim2T1∫−TT[fo(t)−fd(t)]2dt.(1)

图 1. 传统滤波器问题
从物理的角度来看,这样的误差标准当然是合理的,但与流行的观念相反,它绝不是唯一用于误差测量的经得住考验的数学处理方法(文献 5)。
期望的滤波器输出通常是消息函数 fm(t)f_m(t)fm(t)。但是,可能需要消息以外的输出。例如,有人可能要求网络设计能够以秒为单位从噪声中过滤、预测消息,并区分结果。因此,我们可以在一个操作中要求预测、过滤和区分(文献 3)。在这种意义上,一个(滤波器)网络可以被视为一个算子,而不仅仅是一个滤波器(文献 1)。
如果只考虑线性系统,需要设计的统计参数称为相关函数。随机函数 f1(t)f_1(t)f1(t)、f2(t)f_2(t)f2(t) 之间的互相关函数 ϕ12(τ)\\phi_{12}(\\tau)ϕ12(τ) 定义为
ϕ12(τ)=limT→∞12T∫−TTf1(t)f2(t+τ)dt.(2)\\phi_{12}(\\tau)=\\lim_{T\\to\\infty}\\frac{1}{2T}\\int_{-T}^{T}f_1(t)f_2(t+\\tau)\\mathrm{d}t.\\tag{2} ϕ12(τ)=T→∞lim2T1∫−TTf1(t)f2(t+τ)dt.(2)
随机函数 f1(t)f_1(t)f1(t) 的自相关函数 ϕ11(τ)\\phi_{11}(\\tau)ϕ11(τ) 定义为
ϕ11(τ)=limT→∞12T∫−TTf1(t)f1(t+τ)dt.(3)\\phi_{11}(\\tau)=\\lim_{T\\to\\infty}\\frac{1}{2T}\\int_{-T}^{T}f_1(t)f_1(t+\\tau)\\mathrm{d}t.\\tag{3} ϕ11(τ)=T→∞lim2T1∫−TTf1(t)f1(t+τ)dt.(3)
傅里叶变换对 g(t)g(t)g(t)、G(ω)G(\\omega)G(ω) 为
G(ω)=12π∫−∞∞g(t)e−jωtdt(4)G(\\omega)=\\frac{1}{2\\pi}\\int_{-\\infty}^{\\infty}g(t)e^{-\\mathrm{j}\\omega t}\\mathrm{d}t\\tag{4} G(ω)=2π1∫−∞∞g(t)e−jωtdt(4)
和
g(t)=∫−∞∞G(ω)e+jωtdω.(5)g(t)=\\int_{-\\infty}^{\\infty}G(\\omega)e^{+\\mathrm{j}\\omega t}\\mathrm{d}\\omega.\\tag{5} g(t)=∫−∞∞G(ω)e+jωtdω.(5)
拉普拉斯变换同样使用 (4)、(5) 二式,ω\\omegaω 换为
λ=ω+jσ.(6)\\lambda=\\omega+\\mathrm{j}\\sigma.\\tag{6} λ=ω+jσ.(6)
维纳的一个重要定理指出,随机函数 f1(t)f_1(t)f1(t) 功率谱密度由其自相关函数的傅里叶变换给出(文献 3、6),即
Φ11(ω)=12π∫−∞∞ϕ11(τ)e−jωτdτ.(7)\\Phi_{11}(\\omega)=\\frac{1}{2\\pi}\\int_{-\\infty}^{\\infty}\\phi_{11}(\\tau)e^{-\\mathrm{j}\\omega\\tau}\\mathrm{d}\\tau.\\tag{7} Φ11(ω)=2π1∫−∞∞ϕ11(τ)e−jωτdτ.(7)
类似地,我们可以定义随机函数 f1(t)f_1(t)f1(t)、f2(t)f_2(t)f2(t) 的互功率谱 Φ12(ω)\\Phi_{12}(\\omega)Φ12(ω) 为
Φ12(ω)=12π∫−∞∞ϕ12(τ)e−jωτdτ.(8)\\Phi_{12}(\\omega)=\\frac{1}{2\\pi}\\int_{-\\infty}^{\\infty}\\phi_{12}(\\tau)e^{-\\mathrm{j}\\omega\\tau}\\mathrm{d}\\tau.\\tag{8} Φ12(ω)=2π1∫−∞∞ϕ12(τ)e−jωτdτ.(8)
我们定义单位脉冲函数 u(t)u(t)u(t) 为
u(t)=lima→∞aπe−a2t2.u(t)=\\lim_{a\\to\\infty}\\frac{a}{\\sqrt{\\pi}}e^{-a^2t^2}. u(t)=a→∞limπae−a2t2.
如此,我们可以利用 (4) 式得到 u(t)u(t)u(t) 的变换 ∪(ω)\\cup(\\omega)∪(ω) 为
∪(ω)=12π.(9)\\cup(\\omega)=\\frac{1}{2\\pi}.\\tag{9} ∪(ω)=2π1.(9)
现在,若以 h(t)h(t)h(t) 为一线性系统对单位脉冲的响应,可以证明该线性系统对一任意输入 fi(t)f_i(t)fi(t) 的输出 fo(t)f_o(t)fo(t) 由下式给出(文献 3)
fo(t)=∫−∞∞h(σ)fi(t−σ)dσ.(10)f_o(t)=\\int_{-\\infty}^{\\infty}h(\\sigma)f_i(t-\\sigma)\\mathrm{d}\\sigma.\\tag{10} fo(t)=∫−∞∞h(σ)fi(t−σ)dσ.(10)
令 ϵo(t)\\epsilon_o(t)ϵo(t) 为该线性系统对暂态输入 ϵi(t)\\epsilon_i(t)ϵi(t) 的暂态输出。定义线性系统的系统函数 H(ω)H(\\omega)H(ω) 以满足
H(ω)=Eo(ω)Ei(ω)(11)H(\\omega)=\\frac{E_o(\\omega)}{E_i(\\omega)}\\tag{11} H(ω)=Ei(ω)Eo(ω)(11)
可知 H(ω)H(\\omega)H(ω) 和 h(t)h(t)h(t) 具有如下关系
H(ω)=∫−∞∞h(t)e−jωtdt(12)H(\\omega)=\\int_{-\\infty}^{\\infty}h(t)e^{-\\mathrm{j}\\omega t}\\mathrm{d}t\\tag{12} H(ω)=∫−∞∞h(t)e−jωtdt(12)
和
h(t)=12π∫−∞∞H(ω)e+jωtdω,(13)h(t)=\\frac{1}{2\\pi}\\int_{-\\infty}^{\\infty}H(\\omega)e^{+\\mathrm{j}\\omega t}\\mathrm{d}\\omega,\\tag{13} h(t)=2π1∫−∞∞H(ω)e+jωtdω,(13)
除 2π2\\pi2π 项的位置外,同 (4)、(5) 二式。
II. 传输问题
图 1 所示的滤波器设计问题由维纳(文献 1)和李(文献 3)进行了极为详尽的研究,并在 C. A. 斯塔特(文献 8)的实验中得以验证。因此,在本报告中,我们将考虑如图 2 所示的更一般的情况。大多数通信系统中,在将信息引入传输信道之前,存在着修改或者“编码”待传输信息的机会。因此必须以对消息“预失真”或是“预编码”的方式设计 H(ω)H(\\omega)H(ω) 网络,使得“解码”或是滤波网络 G(ω)G(\\omega)G(ω) 产生的输出对于期望输出的均方近似值相比未经处理的消息更佳。
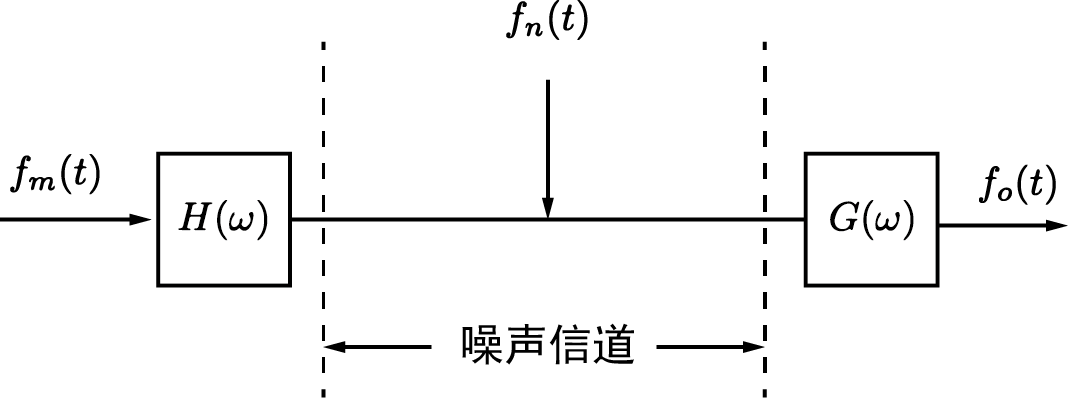
图 2. 传输电路
图 2 中 fo(t)f_o(t)fo(t)、fd(t)f_d(t)fd(t) 之间的均方误差为
ε=limT→∞12T∫−TT[∫−∞∞dσg(σ)fn(t−σ)+∫−∞∞dσg(σ)∫−∞∞dvh(v)fm(t−σ−v)−fd(t)]2.(14)\\varepsilon=\\lim_{T\\to\\infty}\\frac{1}{2T}\\int_{-T}^{T}\\left[ \\begin{aligned} &\\int_{-\\infty}^\\infty\\mathrm{d}{\\sigma g(\\sigma)f_n(t-\\sigma)}\\\\ &+\\int_{-\\infty}^{\\infty}\\mathrm{d}\\sigma g(\\sigma)\\int_{-\\infty}^{\\infty}\\mathrm{d}vh(v)f_m(t-\\sigma-v)\\\\ &-f_d(t) \\end{aligned} \\right]^2.\\tag{14} ε=T→∞lim2T1∫−TT∫−∞∞dσg(σ)fn(t−σ)+∫−∞∞dσg(σ)∫−∞∞dvh(v)fm(t−σ−v)−fd(t)2.(14)
对 (14) 式进行展开,将其以相关函数式进行重写可得
ε=∫−∞∞∫−∞∞dσdvg(σ)g(v)ϕnn(σ−v)+2∫−∞∞∫−∞∞∫−∞∞dξdσdvg(ξ)g(σ)h(v)ϕnm(ξ−σ−v)+∫−∞∞∫−∞∞∫−∞∞∫−∞∞dψdξdσdvg(ψ)h(ξ)g(σ)h(v)ϕmm(ψ+ξ−σ−v)−2∫−∞∞dσg(σ)ϕnd(σ)−2∫−∞∞∫−∞∞dσdvg(σ)h(v)ϕmd(σ+v)+ϕdd(0).(15)\\begin{aligned} \\varepsilon=&\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\mathrm{d}\\sigma\\mathrm{d}vg(\\sigma)g(v)\\phi_{nn}(\\sigma-v)\\\\ &+2\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\mathrm{d}{\\xi}\\mathrm{d}\\sigma\\mathrm{d}vg(\\xi)g(\\sigma)h(v)\\phi_{nm}(\\xi-\\sigma-v)\\\\ &+\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\mathrm{d}\\psi\\mathrm{d}\\xi\\mathrm{d}\\sigma\\mathrm{d}vg(\\psi)h(\\xi)g(\\sigma)h(v)\\phi_{mm}(\\psi+\\xi-\\sigma-v)\\\\ &-2\\int_{-\\infty}^{\\infty}\\mathrm{d}\\sigma g(\\sigma)\\phi_{nd}(\\sigma)\\\\ &-2\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\mathrm{d}\\sigma\\mathrm{d}vg(\\sigma)h(v)\\phi_{md}(\\sigma+v)+\\phi_{dd}(0).\\tag{15} \\end{aligned} ε=∫−∞∞∫−∞∞dσdvg(σ)g(v)ϕnn(σ−v)+2∫−∞∞∫−∞∞∫−∞∞dξdσdvg(ξ)g(σ)h(v)ϕnm(ξ−σ−v)+∫−∞∞∫−∞∞∫−∞∞∫−∞∞dψdξdσdvg(ψ)h(ξ)g(σ)h(v)ϕmm(ψ+ξ−σ−v)−2∫−∞∞dσg(σ)ϕnd(σ)−2∫−∞∞∫−∞∞dσdvg(σ)h(v)ϕmd(σ+v)+ϕdd(0).(15)
要使 (15) 式中 ε\\varepsilonε 最小化,需找到可由物理网络实现的特定脉冲响应函数 g(t)g(t)g(t)、h(t)h(t)h(t),即
g(t),h(t)=0对 t<0.(16)g(t),~h(t)=0\\quad \\text{对}~t<0.\\tag{16} g(t), h(t)=0对 t<0.(16)
此外,还需对编码网络 H(ω)H(\\omega)H(ω) 施以关于平均传输信号功率的额外限制,但此处暂且按下不提。
首先我们尝试假设 H(ω)H(\\omega)H(ω) 为固定值,求解其最优值 G(ω)G(\\omega)G(ω)。这可由令 (15) 式中 g(t)g(t)g(t) 取一可接受的变值 ϵη(t)\\epsilon\\eta(t)ϵη(t),其中
η(t)=0对 t<0(17)\\eta(t)=0\\quad\\text{对}~t<0\\tag{17}η(t)=0对 t<0(17)
且参数 ϵ\\epsilonϵ 相对于 η\\etaη、hhh 独立。也就是说,我们用 g(t)+ϵη(t)g(t)+\\epsilon\\eta(t)g(t)+ϵη(t)、ε+δε\\varepsilon+\\delta\\varepsilonε+δε 分别替换了 (15) 式中的 g(t)g(t)g(t)、ε\\varepsilonε。现在,如果某一确定的 g(t)g(t)g(t) 能够给出最小均方误差,则可确定此最优 g(t)g(t)g(t) 必同时满足
∂(ε+δε)∂ϵ∣ϵ=0=0.(18)\\left.\\frac{\\partial(\\varepsilon+\\delta\\varepsilon)}{\\partial\\epsilon}\\right|_{\\epsilon=0}=0.\\tag{18} ∂ϵ∂(ε+δε)ϵ=0=0.(18)
利用 (15) 式对 (18) 式进行展开可得
∫−∞∞dvg(v)ϕnn(σ−v)+∫−∞∞∫−∞∞dξdvh(v)g(ξ)ϕnm(ξ−σ−v)+∫−∞∞∫−∞∞dξdvh(v)g(ξ)ϕnm(σ−ξ−v)+∫−∞∞∫−∞∞∫−∞∞dψdξdvh(ξ)h(v)g(ψ)ϕmm(ψ+ξ−σ−v)−ϕnd(σ)−∫−∞∞dvh(v)ϕmd(σ+v)=q(σ)(19)\\begin{aligned} &\\int_{-\\infty}^{\\infty}\\mathrm{d}vg(v)\\phi_{nn}(\\sigma-v)+\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\mathrm{d}\\xi\\mathrm{d}vh(v)g(\\xi)\\phi_{nm}(\\xi-\\sigma-v)\\\\ +&\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\mathrm{d}\\xi\\mathrm{d}vh(v)g(\\xi)\\phi_{nm}(\\sigma-\\xi-v)\\\\ +&\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\mathrm{d}\\psi\\mathrm{d}\\xi\\mathrm{d}vh(\\xi)h(v)g(\\psi)\\phi_{mm}(\\psi+\\xi-\\sigma-v)\\\\ -&\\phi_{nd}(\\sigma)-\\int_{-\\infty}^{\\infty}\\mathrm{d}vh(v)\\phi_{md}(\\sigma+v)\\\\ =&q(\\sigma)\\tag{19} \\end{aligned} ++−=∫−∞∞dvg(v)ϕnn(σ−v)+∫−∞∞∫−∞∞dξdvh(v)g(ξ)ϕnm(ξ−σ−v)∫−∞∞∫−∞∞dξdvh(v)g(ξ)ϕnm(σ−ξ−v)∫−∞∞∫−∞∞∫−∞∞dψdξdvh(ξ)h(v)g(ψ)ϕmm(ψ+ξ−σ−v)ϕnd(σ)−∫−∞∞dvh(v)ϕmd(σ+v)q(σ)(19)
其中 q(σ)q(\\sigma)q(σ) 函数定义为
q(σ)=0对 σ>0.(20)q(\\sigma)=0\\quad\\text{对}~\\sigma>0.\\tag{20} q(σ)=0对 σ>0.(20)
现在对(20)式中 σ\\sigmaσ 进行拉普拉斯变换可得
G(λ)F(λ)−Φnd(λ)−H(−λ)Φmd(λ)=Q(λ)(21)G(\\lambda)F(\\lambda)-\\Phi_{nd}(\\lambda)-H(-\\lambda)\\Phi_{md}(\\lambda)=Q(\\lambda)\\tag{21} G(λ)F(λ)−Φnd(λ)−H(−λ)Φmd(λ)=Q(λ)(21)
其中 F(λ)F(\\lambda)F(λ) 函数定义为
F(λ)=H(λ)H(−λ)Φmm(λ)+H(λ)Φnm(λ)+H(−λ)Φmn(λ)+Φnn(λ).(22)F(\\lambda)=H(\\lambda)H(-\\lambda)\\Phi_{mm}(\\lambda)+H(\\lambda)\\Phi_{nm}(\\lambda)+H(-\\lambda)\\Phi_{mn}(\\lambda)+\\Phi_{nn}(\\lambda).\\tag{22} F(λ)=H(λ)H(−λ)Φmm(λ)+H(λ)Φnm(λ)+H(−λ)Φmn(λ)+Φnn(λ).(22)
我们假设 F(λ)F(\\lambda)F(λ) 可以因式分解为
F(λ)=F+(λ)⋅F−(λ)(23)F(\\lambda)=F^+(\\lambda)\\cdot F^-(\\lambda)\\tag{23} F(λ)=F+(λ)⋅F−(λ)(23)
其中 F+(λ)F^+(\\lambda)F+(λ) 包含 λ\\lambdaλ 平面上半部分其所有极点和零点,而 F−(λ)F^-(\\lambda)F−(λ) 则包含 λ\\lambdaλ 平面下半部分其所有极点和零点。借助 (4)、(5)、(6) 式,(21) 式可以重写为
G(λ)F+(λ)−12π∫0∞e−jλtdt∫−∞∞Φnd(ω)+H(−ω)Φmd(ω)F−(ω)e+jωtdω−12π∫−∞0e−jλtdt∫−∞∞Φnd(ω)+H(−ω)Φmd(ω)F−(ω)e+jωtdω=Q(λ)F−(λ).(24)\\begin{aligned} &G(\\lambda)F^+(\\lambda)-\\frac{1}{2\\pi}\\int_0^\\infty e^{-\\mathrm{j}\\lambda t}\\mathrm{d}t\\int_{-\\infty}^{\\infty}\\frac{\\Phi_{nd}(\\omega)+H(-\\omega)\\Phi_{md}(\\omega)}{F^-(\\omega)}e^{+\\mathrm{j}\\omega t}\\mathrm{d}{\\omega}\\\\ -&\\frac{1}{2\\pi}\\int_{-\\infty}^0e^{-\\mathrm{j}\\lambda t}\\mathrm{d}t\\int_{-\\infty}^{\\infty}\\frac{\\Phi_{nd}(\\omega)+H(-\\omega)\\Phi_{md}(\\omega)}{F^-(\\omega)}e^{+\\mathrm{j}\\omega t}\\mathrm{d}{\\omega}\\\\ =&\\frac{Q(\\lambda)}{F^-(\\lambda)}.\\tag{24} \\end{aligned} −=G(λ)F+(λ)−2π1∫0∞e−jλtdt∫−∞∞F−(ω)Φnd(ω)+H(−ω)Φmd(ω)e+jωtdω2π1∫−∞0e−jλtdt∫−∞∞F−(ω)Φnd(ω)+H(−ω)Φmd(ω)e+jωtdωF−(λ)Q(λ).(24)
(24) 式左侧前两项包括了位于 λ\\lambdaλ 平面上半部分的所有可能的极点,而第三项则包含了位于 λ\\lambdaλ 平面下半部分的所有极点。由于 (24) 式右侧仅有下半平面的极点,因此其左侧的前两项之和必为某一常数。可以证明,该常数是零,从而得到
G(λ)=12πF+(λ)∫0∞e−jλtdt∫−∞∞Φnd(ω)+H(−ω)Φmd(ω)F−(ω)e+jωtdω.(25)G(\\lambda)=\\frac{1}{2\\pi F^+(\\lambda)}\\int_{0}^{\\infty}e^{-\\mathrm{j}\\lambda t}\\mathrm{d}t\\int_{-\\infty}^{\\infty}\\frac{\\Phi_{nd}(\\omega)+H(-\\omega)\\Phi_{md}(\\omega)}{F^-(\\omega)}e^{+\\mathrm{j}\\omega t}\\mathrm{d}{\\omega}.\\tag{25} G(λ)=2πF+(λ)1∫0∞e−jλtdt∫−∞∞F−(ω)Φnd(ω)+H(−ω)Φmd(ω)e+jωtdω.(25)
对如图 2 所示固定的 H(λ)H(\\lambda)H(λ) 网络而言,(25) 式给出了解码网络的最优传输函数。由 (25) 式给出的系统函数 G(λ)G(\\lambda)G(λ) 总是可以实现的。
(25) 式有两个有趣的特例。其一是选定 H(λ)=1H(\\lambda)=1H(λ)=1,我们有
F(λ)=Φmm(λ)+Φnm(λ)+Φmn(λ)+Φnn(λ)=Φii(λ).(26)\\begin{aligned} F(\\lambda)&=\\Phi_{mm}(\\lambda)+\\Phi_{nm}(\\lambda)+\\Phi_{mn}(\\lambda)+\\Phi_{nn}(\\lambda)\\\\ &=\\Phi_{ii}(\\lambda).\\tag{26} \\end{aligned} F(λ)=Φmm(λ)+Φnm(λ)+Φmn(λ)+Φnn(λ)=Φii(λ).(26)
这样,F(λ)F(\\lambda)F(λ) 成了 GGG 网络输入的自相关函数的傅里叶变换。对 G(λ)G(\\lambda)G(λ),我们再有
G(λ)=12πΦii+(λ)∫0∞e−jλtdt∫−∞∞Φid(ω)Φii−(ω)e+jωtdω(27)G(\\lambda)=\\frac{1}{2\\pi\\Phi_{ii}^+(\\lambda)}\\int_{0}^{\\infty}e^{-\\mathrm{j}\\lambda t}\\mathrm{d}t\\int_{-\\infty}^{\\infty}\\frac{\\Phi_{id}(\\omega)}{\\Phi_{ii}^-(\\omega)}e^{+\\mathrm{j}\\omega t}\\mathrm{d}\\omega\\tag{27} G(λ)=2πΦii+(λ)1∫0∞e−jλtdt∫−∞∞Φii−(ω)Φid(ω)e+jωtdω(27)
其中 Φid(λ)\\Phi_{id}(\\lambda)Φid(λ) 表示滤波器输入和期望输出之间的互功率谱。(27) 式即为维纳和李所求得的最优滤波器方程,也是图 1 问题的解。
第二个有趣的特例出现在当图 2 中的噪声函数为零时。此时 (25) 式变为
G(λ)=12πH+(λ)Φmm+(λ)∫0∞e−jλtdt∫−∞∞H(−ω)Φmd(ω)H−(ω)Φmm−(ω)e+jωtdω(28)G(\\lambda)=\\frac{1}{2\\pi H^+(\\lambda)\\Phi_{mm}^+(\\lambda)}\\int_0^\\infty e^{-\\mathrm{j}\\lambda t}\\mathrm{d}t\\int_{-\\infty}^{\\infty}\\frac{H(-\\omega)\\Phi_{md}(\\omega)}{H^-(\\omega)\\Phi_{mm}^-(\\omega)}e^{+\\mathrm{j}\\omega t}\\mathrm{d}\\omega\\tag{28} G(λ)=2πH+(λ)Φmm+(λ)1∫0∞e−jλtdt∫−∞∞H−(ω)Φmm−(ω)H(−ω)Φmd(ω)e+jωtdω(28)
其中
H+(λ)H−(λ)=H(λ)H(−λ)(28a)H^+(\\lambda)H^-(\\lambda)=H(\\lambda)H(-\\lambda)\\tag{28a} H+(λ)H−(λ)=H(λ)H(−λ)(28a)
也就是所谓的“最佳补偿器公式”。(28) 式是由 Y. W. 李推导的,尽管他此前从未发表过。
如果考虑将图 2 中 G(ω)G(\\omega)G(ω) 固定,那么利用上面用到的同样方法,我们可以找到最优 H(λ)H(\\lambda)H(λ) 由下式给出
H(λ)=12πG+(λ)Φmm+(λ)∫0∞e−jλtdt∫−∞∞[G(−ω)Φmd(ω)G−(ω)Φmm−(ω)−G+(ω)Φmn(ω)Φmm−(ω)]e+jωtdω(29)H(\\lambda)=\\frac{1}{2\\pi G^+(\\lambda)\\Phi_{mm}^+(\\lambda)}\\int_0^\\infty e^{-\\mathrm{j}\\lambda t}\\mathrm{d}t\\int_{-\\infty}^{\\infty}\\left[\\frac{G(-\\omega)\\Phi_{md}(\\omega)}{G^-(\\omega)\\Phi_{mm}^-(\\omega)}-\\frac{G^+(\\omega)\\Phi_{mn}(\\omega)}{\\Phi_{mm}^-(\\omega)}\\right]e^{+\\mathrm{j}\\omega t}\\mathrm{d}\\omega\\tag{29} H(λ)=2πG+(λ)Φmm+(λ)1∫0∞e−jλtdt∫−∞∞[G−(ω)Φmm−(ω)G(−ω)Φmd(ω)−Φmm−(ω)G+(ω)Φmn(ω)]e+jωtdω(29)
其中
G+(λ)G−(λ)=G(λ)G(−λ).(29a)G^+(\\lambda)G^-(\\lambda)=G(\\lambda)G(-\\lambda).\\tag{29a} G+(λ)G−(λ)=G(λ)G(−λ).(29a)
如果信道噪声为零,或者消息与噪声之间的互相关为零,那么 (29) 式简化为一个最优补偿器公式。
(25) 式给出了固定 H(λ)H(\\lambda)H(λ) 下的最优 G(λ)G(\\lambda)G(λ),而 (29) 式则给出了固定 G(λ)G(\\lambda)G(λ) 下的最优 H(λ)H(\\lambda)H(λ)。如果对 (25)、(29) 式同时求解,则可得图 2 所示传输电路的最优编码-解码网络对。然而,在尝试进行这项求解之前,便利起见,可先解出固定 H(λ)H(\\lambda)H(λ) 和优化 G(λ)G(\\lambda)G(λ) 所得均方误差。将 (19) 式代入 (15) 式得
εmin(固定 H)=ϕdd(0)−∫−∞∞dσg(σ)ϕnd(σ)−∫−∞∞∫−∞∞dσdvg(σ)h(v)ϕmd(σ+v).(30)\\varepsilon_\\text{min}^{(\\text{固定~H})}=\\phi_{dd}(0)-\\int_{-\\infty}^{\\infty}\\mathrm{d}\\sigma g(\\sigma)\\phi_{nd}(\\sigma)-\\int_{-\\infty}^{\\infty}\\int_{-\\infty}^{\\infty}\\mathrm{d}\\sigma\\mathrm{d}v g(\\sigma)h(v)\\phi_{md}(\\sigma+v).\\tag{30} εmin(固定 H)=ϕdd(0)−∫−∞∞dσg(σ)ϕnd(σ)−∫−∞∞∫−∞∞dσdvg(σ)h(v)ϕmd(σ+v).(30)
这个等式可以傅里叶变换的形式重写之,
εmin(固定 H)=∫−∞∞dω[Φdd(ω)−Φnd(ω)G(−ω)−G(−ω)H(−ω)Φmd(ω)].(31)\\varepsilon_\\text{min}^{(\\text{固定~H})}=\\int_{-\\infty}^{\\infty}\\mathrm{d}\\omega\\left[\\Phi_{dd}(\\omega)-\\Phi_{nd}(\\omega)G(-\\omega)-G(-\\omega)H(-\\omega)\\Phi_{md}(\\omega)\\right].\\tag{31} εmin(固定 H)=∫−∞∞dω[Φdd(ω)−Φnd(ω)G(−ω)−G(−ω)H(−ω)Φmd(ω)].(31)
一定要记住,(30)、(31) 式中的 g(σ)g(\\sigma)g(σ)、G(ω)G(\\omega)G(ω) 不是任意取的,而是 (19) 式的解。
III. 长延迟的解
在求解图 2 所示的最优网络对时,我们假设了消息和信道噪声之间互相关为零。我们进一步假设解是长延迟的,即是说期望的输出是延迟之后的消息。于是有
fd(t)=fm(t−a),a→∞(32)f_d(t)=f_m(t-a),\\quad a\\to\\infty\\tag{32}fd(t)=fm(t−a),a→∞(32)
和
Φmd(ω)=Φmm(ω)e−jωa,a→∞.(33)\\Phi_{md}(\\omega)=\\Phi_{mm}(\\omega)e^{-\\mathrm{j}\\omega a},\\quad a\\to\\infty.\\tag{33} Φmd(ω)=Φmm(ω)e−jωa,a→∞.(33)
在此条件之下,(25) 式可重写为
G(ω)→H(−ω)Φmm(ω)e−jaω∣H(ω)∣2Φmm(ω)+Φnn(ω),a→∞.(34)G(\\omega)\\to\\frac{H(-\\omega)\\Phi_{mm}(\\omega)e^{-\\mathrm{j}a\\omega}}{\\left|H(\\omega)\\right|^2\\Phi_{mm}(\\omega)+\\Phi_{nn}(\\omega)},\\quad a\\to \\infty.\\tag{34} G(ω)→∣H(ω)∣2Φmm(ω)+Φnn(ω)H(−ω)Φmm(ω)e−jaω,a→∞.(34)
由于在允许长延迟的情况下可以得到最好的滤波结果(文献 3),故将 (34) 式代入 (31) 式将得到最小的误差,即所谓的不可消误差。因此,我们最终有
εirr(固定 H)=∫−∞∞Φmm(ω)Φnn(ω)∣H(ω)∣2Φmm(ω)+Φnn(ω)dω.(35)\\varepsilon_\\text{irr}^{(\\text{固定~H})}=\\int_{-\\infty}^{\\infty}\\frac{\\Phi_{mm}(\\omega)\\Phi_{nn}(\\omega)}{\\left|H(\\omega)\\right|^2\\Phi_{mm}(\\omega)+\\Phi_{nn}(\\omega)}\\mathrm{d}\\omega.\\tag{35} εirr(固定 H)=∫−∞∞∣H(ω)∣2Φmm(ω)+Φnn(ω)Φmm(ω)Φnn(ω)dω.(35)
注意,不可消误差只依赖于传递函数 H(ω)H(\\omega)H(ω) 的幅度,而非相位。由 (34) 式可知,因固定 H(ω)H(\\omega)H(ω) 引起的任何相位贡献都将被最优解码网络 G(ω)G(\\omega)G(ω) 去除。
对于给定的 H(ω)H(\\omega)H(ω),(35) 式将给出根据 (34) 式设计的网络 G(ω)G(\\omega)G(ω) 产生的传输误差。因此,我们必须找到使 (35) 式误差最小的 H(ω)H(\\omega)H(ω),同时保持平均传输信号功率不变。也就是说,鉴于 ∣H(ω)∣2Φmm(ω)\\left|H(\\omega)\\right|^2\\Phi_{mm}(\\omega)∣H(ω)∣2Φmm(ω) 代表着编码网络输出的功率谱密度,我们必须要令
∫−∞∞∣H(ω)∣2Φmm(ω)dω=c1.(36)\\int_{-\\infty}^\\infty\\left|H(\\omega)\\right|^2\\Phi_{mm}(\\omega)\\mathrm{d}\\omega=c_1.\\tag{36} ∫−∞∞∣H(ω)∣2Φmm(ω)dω=c1.(36)
若令
[y(ω)]2=∣H(ω)∣2Φmm(ω)(37)\\left[y(\\omega)\\right]^2=\\left|H(\\omega)\\right|^2\\Phi_{mm}(\\omega)\\tag{37} [y(ω)]2=∣H(ω)∣2Φmm(ω)(37)
则 (35)、(36) 式可重写为
εirr2=∫0∞Φmm(ω)Φnn(ω)[y(ω)]2+Φnn(ω)dω(38)\\frac{\\varepsilon_{\\text{irr}}}{2}=\\int_0^\\infty\\frac{\\Phi_{mm}(\\omega)\\Phi_{nn}(\\omega)}{\\left[y(\\omega)\\right]^2+\\Phi_{nn}(\\omega)}\\mathrm{d}\\omega\\tag{38} 2εirr=∫0∞[y(ω)]2+Φnn(ω)Φmm(ω)Φnn(ω)dω(38)
和
∫0∞[y(ω)]2dω=c12.(39)\\int_0^\\infty\\left[y(\\omega)\\right]^2\\mathrm{d}\\omega=\\frac{c_1}{2}.\\tag{39} ∫0∞[y(ω)]2dω=2c1.(39)
我们现在寻找的是使 (38) 式最小并且满足 (39) 式的实函数 y(ω)y(\\omega)y(ω)。这就是所谓变分法的等周条件。通过应用常用的技巧(文献 9)可得
∣H(ω)∣2Φmm(ω)=−Φnn(ω)+1γΦmm(ω)Φnn(ω)(40a)\\left|H(\\omega)\\right|^2\\Phi_{mm}(\\omega)=-\\Phi_{nn}(\\omega)+\\frac{1}{\\sqrt{\\gamma}}\\sqrt{\\Phi_{mm}(\\omega)\\Phi_{nn}(\\omega)}\\tag{40a} ∣H(ω)∣2Φmm(ω)=−Φnn(ω)+γ1Φmm(ω)Φnn(ω)(40a)
和
∣H(ω)∣2Φmm(ω)=0(40b)\\left|H(\\omega)\\right|^2\\Phi_{mm}(\\omega)=0\\tag{40b} ∣H(ω)∣2Φmm(ω)=0(40b)
其中 γ\\gammaγ 为一满足 (39) 式的常数。若 (39) 式右侧大于零则用 (40a) 式,否则必须使用 (40b) 式。物理意义上,这意味着 H(ω)H(\\omega)H(ω) 可能包含截止带。然而由于假设通过 H(ω)H(\\omega)H(ω) 到 G(ω)G(\\omega)G(ω) 有无限长的延迟时间,因而此截止带的存在并不违反佩利-维纳定理(文献 1、10、11)。
IV. 结果讨论
作为对第 III 节结果的检查,设有噪声谱
Φnn(ω)=a2(41)\\Phi_{nn}(\\omega)=a^2\\tag{41}Φnn(ω)=a2(41)
和消息谱
Φmm(ω)=β/πω2+β2.(42)\\Phi_{mm}(\\omega)=\\frac{\\beta/\\pi}{\\omega^2+\\beta^2}.\\tag{42} Φmm(ω)=ω2+β2β/π.(42)
取 2a2β=1/5π2a^2\\beta=1/5~\\pi2a2β=1/5 π,c1=1c_1=1c1=1 时,(38) 式给出的均方误差为 0.2850.2850.285。在不进行编码且使用相同的平均信号功率情况下,令 ∣H(ω)∣2=1\\left|H(\\omega)\\right|^2=1∣H(ω)∣2=1,由 (35) 式可算得均方误差为 0.3020.3020.302。因此,最优编码网络对于提升传输性能有一定的贡献,但是不多。对于所引用的特例,当超过 ω=8.45β\\omega=8.45\\betaω=8.45β 之后,H(ω)H(\\omega)H(ω) 无法进行传输;当噪声电平提高 5 倍,此上限截止频率下降到 ω=3.25β\\omega=3.25\\betaω=3.25β。
可以看出,图 2 可以表示使用幅度调制的通信电路(参见文献 4)。使用频率调制会令问题复杂化,但也有人提出形如
Φnn(ω)=a2ω2(43)\\Phi_{nn}(\\omega)=a^2\\omega^2\\tag{43}Φnn(ω)=a2ω2(43)
的噪声谱可能是有意义的。研究发现,利用 (42) 式的消息谱和 (43) 式的噪声谱,对于采用最优编码或者“预强调”的网络只能得到适度的改善。
上述均方误差的适度改善部分原因在于假设了特定的频谱。因此,在某些情况下,使用适当的编码网络可能会实现相当大的改进。
参考文献
- N. Wiener: The Extrapolation, Interpolation, and Smoothing of Stationary Time Series with Engineering Applications, John Wiley, New York, 1949
- N. Wiener: Cybernetics, John Wiley, New York, 1948
- Y. W. Lee: Course 6.563, Statistical Theory of Communication, Class Notes, M.I.T. unpublished
- J. P. Costas: Interference Filtering, Technical Report No. 185, Research Laboratory of Electronics, M.I.T. March 1951
- Y. W. Lee: Memorandum on Error Criteria in Filter Design, unpublished
- N. Wiener: Generalized Harmonic Analysis, Acta Math. 55, 117-258, 1930
- Y. W. Lee, C. A. Stutt: Statistical Prediction of Noise, Techinical Report No. 129, Research Laboratory of Electronics, M.I.T. July 1949
- C. A. Stutt: An Experimental Study of Optimum Linear Systems, Doctoral Thesis, Dept. of Electrical Engineering, M.I.T. May 15, 1951
- H. Margenau, G. M. Murphy: The Mathematics of Physics and Chemistry, Van Nostrand, New York, 1943
- G. E. Valley, Jr., H. Wallman: Vacuum Tube Amplifiers, McGraw-Hill, New York, 1948
- R. Paley, N. Wiener: Fourier Transforms in the Complex Domain, Am. Math. Soc. Colloq. Pub. 19, 1934
致谢
笔者希望向麻省理工学院电子研究实验室的 Y. W. Lee 教授、C. A. Stutt 博士和 C. A. Desoer 先生致谢,感谢他们提出的许多有益的意见和建议。
© 1952 J. P. Costas
© 2023 Conmajia
-
IRE(无线电工程师学会)是 IEEE(电气电子工程师学会)的前身,于 1912 年成立。1963 年 IRE 与 AIEE(美国电气工程师学会)合并成立了 IEEE。 ↩︎
-
由于翻译人员水平差异和民间音译习惯,David Huffman 常被译为“大卫·哈夫曼”。根据商务印书馆出版的《(外国)人名翻译手册》系列,正式的译名应为“戴维·赫夫曼”。 ↩︎


