优先、双端队列-我的基础算法刷题之路(八)


本篇博客旨在整理记录自已对优先队列、双端队列的一些总结,以及刷题的解题思路,同时希望可给小伙伴一些帮助。本人也是算法小白,水平有限,如果文章中有什么错误之处,希望小伙伴们可以在评论区指出来,共勉 💪。
本篇内容接上篇:http://t.csdn.cn/akLoF
文章目录
-
- 一、双端队列
-
- 1.概述
- 2.接口定义
- 3.代码实现
- 二、优先级队列
-
- 1.无序数组实现
- 2.有序数组实现
- 3.堆实现
- 三、阻塞队列
-
- 1.单锁实现
- 2.双锁实现
- 最后
一、双端队列
1.概述
对比如图:
| 定义 | 特点 | |
|---|---|---|
| 队列 | 一端删除(头)另一端添加(尾) | First In First Out |
| 双端队列 | 两端都可以删除、添加 | |
| 优先队列 | 优先级高者先出队 | |
| 延时队列 | 根据延时时间确定优先级 | |
| 并发非阻塞队列 | 队列空或满时不阻塞 | |
| 并发阻塞队列 | 队列空时删除阻塞、队列满时添加阻塞 |
注1:
- Java 中 LinkedList 即为典型双端队列实现,不过它同时实现了Queue 接口,也提供了栈的 push pop等方法
注2:
不同语言,操作双端队列得方法命名有所不同,见下表
操作 Java JavaScript C++ leetCode641 尾部插入 offerLast push push_back insertLast 头部插入 offerFirst unshift push_front insertFront 尾部移除 pollLast pop pop_back deleteLast 头部移除 pollFirst shift pop_front deleteFront 尾部获取 peekLast at(-1) back getRear 头部获取 peekFirst at(0) front getFront
- 常见的还有enqueue 入队、dequeue 出队
2.接口定义
public interface Deque<E> {boolean offerFirst(E e);boolean offerLast(E e);E pollFirst();E pollLast();E peekFirst();E peekLast();boolean isEmpty();boolean isFull();
}
3.代码实现
链表实现
/* 基于环形链表的双端队列* @param <E> 元素类型*/
public class LinkedListDeque<E> implements Deque<E>, Iterable<E> {@Overridepublic boolean offerFirst(E e) {if (isFull()) {return false;}size++;Node<E> a = sentinel;Node<E> b = sentinel.next;Node<E> offered = new Node<>(a, e, b);a.next = offered;b.prev = offered;return true;}@Overridepublic boolean offerLast(E e) {if (isFull()) {return false;}size++;Node<E> a = sentinel.prev;Node<E> b = sentinel;Node<E> offered = new Node<>(a, e, b);a.next = offered;b.prev = offered;return true;}@Overridepublic E pollFirst() {if (isEmpty()) {return null;}Node<E> a = sentinel;Node<E> polled = sentinel.next;Node<E> b = polled.next;a.next = b;b.prev = a;size--;return polled.value;}@Overridepublic E pollLast() {if (isEmpty()) {return null;}Node<E> polled = sentinel.prev;Node<E> a = polled.prev;Node<E> b = sentinel;a.next = b;b.prev = a;size--;return polled.value;}@Overridepublic E peekFirst() {if (isEmpty()) {return null;}return sentinel.next.value;}@Overridepublic E peekLast() {if (isEmpty()) {return null;}return sentinel.prev.value;}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == capacity;}@Overridepublic Iterator<E> iterator() {return new Iterator<E>() {Node<E> p = sentinel.next;@Overridepublic boolean hasNext() {return p != sentinel;}@Overridepublic E next() {E value = p.value;p = p.next;return value;}};}static class Node<E> {Node<E> prev;E value;Node<E> next;public Node(Node<E> prev, E value, Node<E> next) {this.prev = prev;this.value = value;this.next = next;}}Node<E> sentinel = new Node<>(null, null, null);int capacity;int size;public LinkedListDeque(int capacity) {sentinel.next = sentinel;sentinel.prev = sentinel;this.capacity = capacity;}
}
数组实现
/* 基于循环数组实现, 特点* <ul>* <li>tail 停下来的位置不存储, 会浪费一个位置</li>* </ul>* @param <E>*/
public class ArrayDeque1<E> implements Deque<E>, Iterable<E> {/*ht0 1 2 3b a*/@Overridepublic boolean offerFirst(E e) {if (isFull()) {return false;}head = dec(head, array.length);array[head] = e;return true;}@Overridepublic boolean offerLast(E e) {if (isFull()) {return false;}array[tail] = e;tail = inc(tail, array.length);return true;}@Overridepublic E pollFirst() {if (isEmpty()) {return null;}E e = array[head];array[head] = null;head = inc(head, array.length);return e;}@Overridepublic E pollLast() {if (isEmpty()) {return null;}tail = dec(tail, array.length);E e = array[tail];array[tail] = null;return e;}@Overridepublic E peekFirst() {if (isEmpty()) {return null;}return array[head];}@Overridepublic E peekLast() {if (isEmpty()) {return null;}return array[dec(tail, array.length)];}@Overridepublic boolean isEmpty() {return head == tail;}@Overridepublic boolean isFull() {if (tail > head) {return tail - head == array.length - 1;} else if (tail < head) {return head - tail == 1;} else {return false;}}@Overridepublic Iterator<E> iterator() {return new Iterator<E>() {int p = head;@Overridepublic boolean hasNext() {return p != tail;}@Overridepublic E next() {E e = array[p];p = inc(p, array.length);return e;}};}E[] array;int head;int tail;@SuppressWarnings("unchecked")public ArrayDeque1(int capacity) {array = (E[]) new Object[capacity + 1];}static int inc(int i, int length) {if (i + 1 >= length) {return 0;}return i + 1;}static int dec(int i, int length) {if (i - 1 < 0) {return length - 1;}return i - 1;}
}
数组实现中,如果存储的时基本类型,那么无需考虑内存释放,例如

但如果存储的是引用类型,应当设置该位置得引用为null,以便内存及时释放

二、优先级队列
1.无序数组实现
要点
- 入队保持顺序
- 出队前找到优先级最高的出队,相当于一次选择排序
public class PriorityQueue1<E extends Priority> implements Queue<E> {Priority[] array;int size;public PriorityQueue1(int capacity) {array = new Priority[capacity];}@Override // O(1)public boolean offer(E e) {if (isFull()) {return false;}array[size++] = e;return true;}// 返回优先级最高的索引值private int selectMax() {int max = 0;for (int i = 1; i < size; i++) {if (array[i].priority() > array[max].priority()) {max = i;}}return max;}@Override // O(n)public E poll() {if (isEmpty()) {return null;}int max = selectMax();E e = (E) array[max];remove(max);return e;}private void remove(int index) {if (index < size - 1) {System.arraycopy(array, index + 1,array, index, size - 1 - index);}array[--size] = null; // help GC}@Overridepublic E peek() {if (isEmpty()) {return null;}int max = selectMax();return (E) array[max];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == array.length;}
}
2.有序数组实现
要点
- 入队后排好序,优先级最高的排列在尾部
- 出队只需删除尾部元素即可
public class PriorityQueue2<E extends Priority> implements Queue<E> {Priority[] array;int size;public PriorityQueue2(int capacity) {array = new Priority[capacity];}// O(n)@Overridepublic boolean offer(E e) {if (isFull()) {return false;}insert(e);size++;return true;}// 一轮插入排序private void insert(E e) {int i = size - 1;while (i >= 0 && array[i].priority() > e.priority()) {array[i + 1] = array[i];i--;}array[i + 1] = e;}// O(1)@Overridepublic E poll() {if (isEmpty()) {return null;}E e = (E) array[size - 1];array[--size] = null; // help GCreturn e;}@Overridepublic E peek() {if (isEmpty()) {return null;}return (E) array[size - 1];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == array.length;}
}
3.堆实现
计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。堆的特性如下
- 在大顶堆中,任意节点 C 与它的父节点 P 符合 P.value≥C.valueP.value \\geq C.valueP.value≥C.value
- 而小顶堆中,任意节点 C 与它的父节点 P 符合 P.value≤C.valueP.value \\leq C.valueP.value≤C.value
- 最顶层的节点(没有父亲)称之为 root 根节点
例1 - 满二叉树(Full Binary Tree)特点:每一层都是填满的

例2 - 完全二叉树(Complete Binary Tree)特点:最后一层可能未填满,靠左对齐

例3 - 大顶堆

例4 - 小顶堆

完全二叉树可以使用数组来表示

特征
- 如果从索引 0 开始存储节点数据
- 节点 i 的父结点为 floor((i−1)/2)floor((i-1)/2)floor((i−1)/2),当i>0i > 0i>0时
- 节点 i 的左子节点为 2i+12i+12i+1,右子节点为2i+22i+22i+2,当然它们得 <size< size<size
- 如果从索引 1 开始存储节点数据
- 节点 iii 的父结点为 floor(i/2)floor(i/2)floor(i/2),当 i>1i>1i>1 时
- 节点 iii 的左子节点为 2i2i2i,右子节点为 2i+12i+12i+1,同样得 <size< size<size
代码
public class PriorityQueue4<E extends Priority> implements Queue<E> {Priority[] array;int size;public PriorityQueue4(int capacity) {array = new Priority[capacity];}@Overridepublic boolean offer(E offered) {if (isFull()) {return false;}int child = size++;int parent = (child - 1) / 2;while (child > 0 && offered.priority() > array[parent].priority()) {array[child] = array[parent];child = parent;parent = (child - 1) / 2;}array[child] = offered;return true;}private void swap(int i, int j) {Priority t = array[i];array[i] = array[j];array[j] = t;}@Overridepublic E poll() {if (isEmpty()) {return null;}swap(0, size - 1);size--;Priority e = array[size];array[size] = null;shiftDown(0); return (E) e;}void shiftDown(int parent) {int left = 2 * parent + 1;int right = left + 1;int max = parent;if (left < size && array[left].priority() > array[max].priority()) {max = left;}if (right < size && array[right].priority() > array[max].priority()) {max = right;}if (max != parent) {swap(max, parent);shiftDown(max);}}@Overridepublic E peek() {if (isEmpty()) {return null;}return (E) array[0];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == array.length;}
}
三、阻塞队列
之前的队列在很多场景下都不能很好地工作,例如
- 大部分场景要求分离向队列放入(生产者)、从队列拿出(消费者)两个角色、它们得由不同的线程来担当,而之前的实现根本没有考虑线程安全问题
- 队列为空,那么在之前的实现里会返回 null,如果就是硬要拿到一个元素呢?只要不断循环尝试
- 队列为满,那么再之前的实现里会返回 false,如果就是硬要塞入一个元素呢?只能不断循环尝试
因此我们需要解决的问题有
- 用锁保证线程的安全
- 用条件变量让等待非空线程与等待不满线程进入等待状态,而不是不断循环尝试,让 CPU 空转
有同学对线程安全还没有足够的认识,下面举一个反例,两个线程都要执行入队操作(几乎在同一时刻)
public class TestThreadUnsafe {private final String[] array = new String[10];private int tail = 0;public void offer(String e) {array[tail] = e;tail++;}@Overridepublic String toString() {return Arrays.toString(array);}public static void main(String[] args) {TestThreadUnsafe queue = new TestThreadUnsafe();new Thread(()-> queue.offer("e1"), "t1").start();new Thread(()-> queue.offer("e2"), "t2").start();}
}
执行的时间序列如下,假设初始状态 tail = 0,在执行过程中由于 CPU 在两个线程之间切换,造成了指令交错。
| 线程1 | 线程2 | 说明 |
|---|---|---|
| array[tail]=e1 | 线程1 向 tail 位置加入 e1 这个元素,但还没来得及执行 tail++ | |
| array[tail]=e2 | 线程2 向 tail 位置加入 e2 这个元素,覆盖掉了 e1 | |
| tail++ | tail 自增为1 | |
| tail++ | tail 自增为2 | |
| 最后状态 tail 为 2,数组为 [e2, null, null …] |
糟糕的是,由于指令交错的顺序不同,得到的结果不止以上一种,宏观上造成混乱的效果。
1.单锁实现
Java 中要防止代码段交错执行,需要使用锁,有两种选择
- synchronized 代码块,属于关键字级别提供锁保护,功能少
- ReentrantLock 类,功能丰富
以 ReentrantLock 为例
ReentrantLock lock = new ReentrantLock();public void offer(String e) {lock.lockInterruptibly();try {array[tail] = e;tail++;} finally {lock.unlock();}
}
只要两个线程执行上段代码时,锁对象是同一个,就能保证 try 块内的代码的执行不会出现指令交错现象,即执行顺序只可能是下面两种情况之一。
| 线程1 | 线程2 | 说明 |
|---|---|---|
| lock.lockInterruptibly() | t1对锁对象上锁 | |
| array[tail]=e1 | ||
| lock.lockInterruptibly() | 即使 CPU 切换到线程2,但由于t1已经对该对象上锁,因此线程2卡在这儿进不去 | |
| tail++ | 切换回线程1 执行后续代码 | |
| lock.unlock() | 线程1 解锁 | |
| array[tail]=e2 | 线程2 此时才能获得锁,执行它的代码 | |
| tail++ |
- 另一种情况是线程2 先获得锁,线程1 被挡在外面
- 要明白保护的本质,本例中是保护的是 tail 位置读写的安全
事情还没有完,上面的例子是队列还没有放满的情况,考虑下面的代码(这回锁同时保护了 tail 和 size 的读写安全)
ReentrantLock lock = new ReentrantLock();
int size = 0;public void offer(String e) {lock.lockInterruptibly();try {if(isFull()) {// 满了怎么办?}array[tail] = e;tail++;size++;} finally {lock.unlock();}
}private boolean isFull() {return size == array.length;
}
之前是返回 false 表示添加失败,前面分析过想达到这么一种效果:
- 在队列满时,不是立刻返回,而是当前线程进入等待
- 什么时候队列不满了,再唤醒这个等待的线程,从上次的代码处继续向下运行
ReentrantLock 可以配合条件变量来实现,代码进化为:
ReentrantLock lock = new ReentrantLock();
Condition tailWaits = lock.newCondition(); // 条件变量
int size = 0;public void offer(String e) {lock.lockInterruptibly();try {while (isFull()) {tailWaits.await(); // 当队列满时, 当前线程进入 tailWaits 等待}array[tail] = e;tail++;size++;} finally {lock.unlock();}
}private boolean isFull() {return size == array.length;
}
- 条件变量底层也是个队列,用来存储这些需要等待的线程,当队列满了,就会将 offer 线程加入条件队列,并暂时释放锁
- 将来我们的队列如果不满了(由 poll 线程那边得知)可以调用 tailWaits.signal() 来唤醒 tailWaits 中首个等待的线程,被唤醒的线程会再次抢到锁,从上次 await 处继续向下运行
思考为何要用 while 而不是 if,设队列容量是 3?
| 操作前 | offer(4) | offer(5) | poll() | 操作后 |
|---|---|---|---|---|
| [1 2 3] | 队列满,进入tailWaits 等待 | [1 2 3] | ||
| [1 2 3] | 取走 1,队列不满,唤醒线程 | [2 3] | ||
| [2 3] | 抢先获得锁,发现不满,放入 5 | [2 3 5] | ||
| [2 3 5] | 从上次等待处直接向下执行 | [2 3 5 ?] |
关键点:
- 从 tailWaits 中唤醒的线程,会与新来的 offer 的线程争抢锁,谁能抢到是不一定的,如果后者先抢到,就会导致条件又发生变化
- 这种情况称之为虚假唤醒,唤醒后应该重新检查条件,看是不是得重新进入等待
最后的实现代码
/* 单锁实现* @param <E> 元素类型*/
public class BlockingQueue1<E> implements BlockingQueue<E> {private final E[] array;private int head = 0;private int tail = 0;private int size = 0; // 元素个数@SuppressWarnings("all")public BlockingQueue1(int capacity) {array = (E[]) new Object[capacity];}ReentrantLock lock = new ReentrantLock();Condition tailWaits = lock.newCondition();Condition headWaits = lock.newCondition();@Overridepublic void offer(E e) throws InterruptedException {lock.lockInterruptibly();try {while (isFull()) {tailWaits.await();}array[tail] = e;if (++tail == array.length) {tail = 0;}size++;headWaits.signal();} finally {lock.unlock();}}@Overridepublic void offer(E e, long timeout) throws InterruptedException {lock.lockInterruptibly();try {long t = TimeUnit.MILLISECONDS.toNanos(timeout);while (isFull()) {if (t <= 0) {return;}t = tailWaits.awaitNanos(t);}array[tail] = e;if (++tail == array.length) {tail = 0;}size++;headWaits.signal();} finally {lock.unlock();}}@Overridepublic E poll() throws InterruptedException {lock.lockInterruptibly();try {while (isEmpty()) {headWaits.await();}E e = array[head];array[head] = null; // help GCif (++head == array.length) {head = 0;}size--;tailWaits.signal();return e;} finally {lock.unlock();}}private boolean isEmpty() {return size == 0;}private boolean isFull() {return size == array.length;}
}
- public void offer(E e, long timeout) throws InterruptedException 是带超时的版本,可以只等待一段时间,而不是永久等下去,类似的 poll 也可以做带超时的版本,这个留给大家了。
注意
- JDK 中 BlockingQueue 接口的方法命名与我的示例有些差异
- 方法 offer(E e) 是非阻塞的实现,阻塞实现方法为 put(E e)
- 方法 poll() 是非阻塞的实现,阻塞实现方法为 take()
2.双锁实现
单锁的缺点在于:
- 生产和消费几乎是不冲突的,唯一冲突的是生产者和消费者它们有可能同时修改 size
- 冲突的主要是生产者之间:多个 offer 线程修改 tail
- 冲突的还有消费者之间:多个 poll 线程修改 head
如果希望进一步提高性能,可以用两把锁:
- 一把锁保护 tail
- 另一把锁保护 head
ReentrantLock headLock = new ReentrantLock(); // 保护 head 的锁
Condition headWaits = headLock.newCondition(); // 队列空时,需要等待的线程集合ReentrantLock tailLock = new ReentrantLock(); // 保护 tail 的锁
Condition tailWaits = tailLock.newCondition(); // 队列满时,需要等待的线程集合
先看看 offer 方法的初步实现
@Override
public void offer(E e) throws InterruptedException {tailLock.lockInterruptibly();try {// 队列满等待while (isFull()) {tailWaits.await();}// 不满则入队array[tail] = e;if (++tail == array.length) {tail = 0;}// 修改 size (有问题)size++;} finally {tailLock.unlock();}
}
上面代码的缺点是 size 并不受 tailLock 保护,tailLock 与 headLock 是两把不同的锁,并不能实现互斥的效果。因此,size 需要用下面的代码保证原子性。
AtomicInteger size = new AtomicInteger(0); // 保护 size 的原子变量size.getAndIncrement(); // 自增
size.getAndDecrement(); // 自减
代码修改为
@Override
public void offer(E e) throws InterruptedException {tailLock.lockInterruptibly();try {// 队列满等待while (isFull()) {tailWaits.await();}// 不满则入队array[tail] = e;if (++tail == array.length) {tail = 0;}// 修改 sizesize.getAndIncrement();} finally {tailLock.unlock();}
}
对称地,可以写出 poll 方法
@Override
public E poll() throws InterruptedException {E e;headLock.lockInterruptibly();try {// 队列空等待while (isEmpty()) {headWaits.await();}// 不空则出队e = array[head];if (++head == array.length) {head = 0;}// 修改 sizesize.getAndDecrement();} finally {headLock.unlock();}return e;
}
下面来看一个难题,就是如何通知 headWaits 和 tailWaits 中等待的线程,比如 poll 方法拿走一个元素,通知 tailWaits:我拿走一个,不满了噢,你们可以放了,因此代码改为
@Override
public E poll() throws InterruptedException {E e;headLock.lockInterruptibly();try {// 队列空等待while (isEmpty()) {headWaits.await();}// 不空则出队e = array[head];if (++head == array.length) {head = 0;}// 修改 sizesize.getAndDecrement();// 通知 tailWaits 不满(有问题)tailWaits.signal();} finally {headLock.unlock();}return e;
}
问题在于要使用这些条件变量的 await(), signal() 等方法需要先获得与之关联的锁,上面的代码若直接运行会出现以下错误:
java.lang.IllegalMonitorStateException
那有同学说,加上锁不就行了吗,于是写出了下面的代码
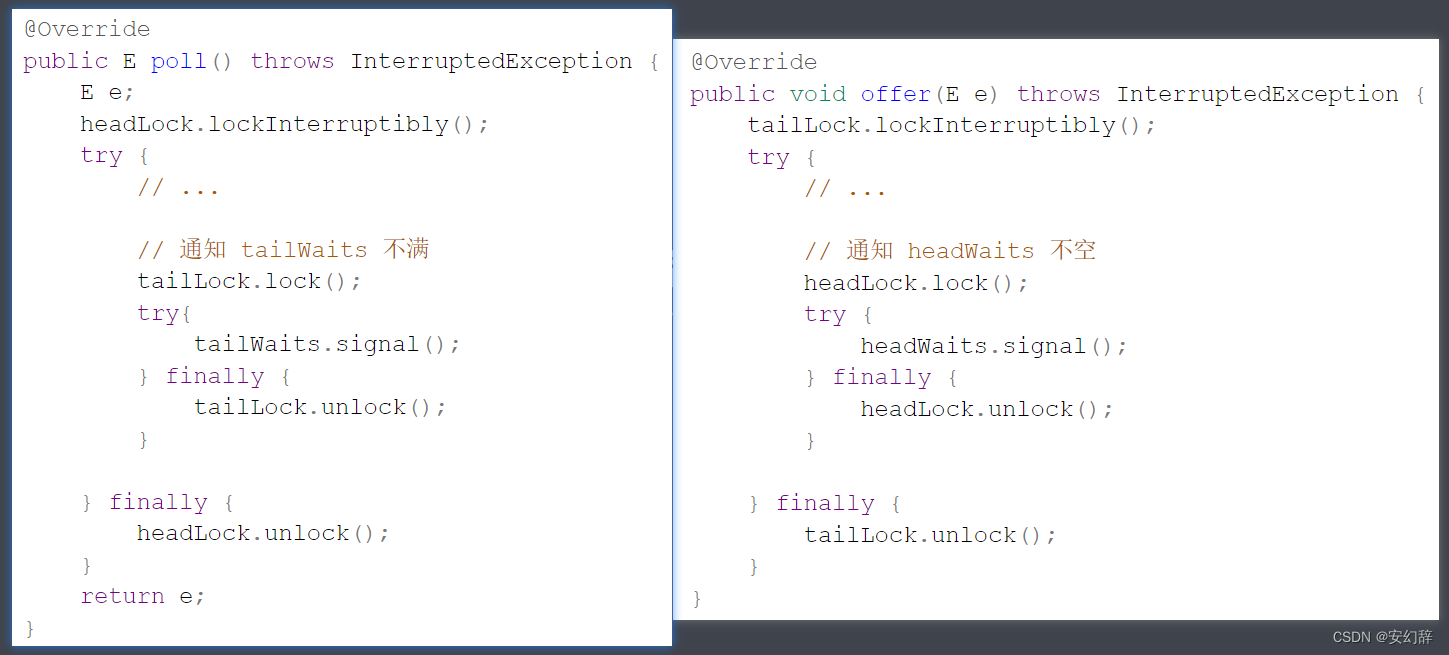
发现什么问题了?两把锁这么嵌套使用,非常容易出现死锁,如下所示

因此得避免嵌套,两段加锁的代码变成了下面平级的样子

性能还可以进一步提升
-
代码调整后 offer 并没有同时获取 tailLock 和 headLock 两把锁,因此两次加锁之间会有空隙,这个空隙内可能有其它的 offer 线程添加了更多的元素,那么这些线程都要执行 signal(),通知 poll 线程队列非空吗?
- 每次调用 signal() 都需要这些 offer 线程先获得 headLock 锁,成本较高,要想法减少 offer 线程获得 headLock 锁的次数
- 可以加一个条件:当 offer 增加前队列为空,即从 0 变化到不空,才由此 offer 线程来通知 headWaits,其它情况不归它管
-
队列从 0 变化到不空,会唤醒一个等待的 poll 线程,这个线程被唤醒后,肯定能拿到 headLock 锁,因此它具备了唤醒 headWaits 上其它 poll 线程的先决条件。如果检查出此时有其它 offer 线程新增了元素(不空,但不是从0变化而来),那么不妨由此 poll 线程来唤醒其它 poll 线程
这个技巧被称之为级联通知(cascading notifies),类似的原因
- 在 poll 时队列从满变化到不满,才由此 poll 线程来唤醒一个等待的 offer 线程,目的也是为了减少 poll 线程对 tailLock 上锁次数,剩下等待的 offer 线程由这个 offer 线程间接唤醒
最终的代码为
public class BlockingQueue2<E> implements BlockingQueue<E> {private final E[] array;private int head = 0;private int tail = 0;private final AtomicInteger size = new AtomicInteger(0);ReentrantLock headLock = new ReentrantLock();Condition headWaits = headLock.newCondition();ReentrantLock tailLock = new ReentrantLock();Condition tailWaits = tailLock.newCondition();public BlockingQueue2(int capacity) {this.array = (E[]) new Object[capacity];}@Overridepublic void offer(E e) throws InterruptedException {int c;tailLock.lockInterruptibly();try {while (isFull()) {tailWaits.await();}array[tail] = e;if (++tail == array.length) {tail = 0;} c = size.getAndIncrement();// a. 队列不满, 但不是从满->不满, 由此offer线程唤醒其它offer线程if (c + 1 < array.length) {tailWaits.signal();}} finally {tailLock.unlock();}// b. 从0->不空, 由此offer线程唤醒等待的poll线程if (c == 0) {headLock.lock();try {headWaits.signal();} finally {headLock.unlock();}}}@Overridepublic E poll() throws InterruptedException {E e;int c;headLock.lockInterruptibly();try {while (isEmpty()) {headWaits.await(); }e = array[head]; if (++head == array.length) {head = 0;}c = size.getAndDecrement();// b. 队列不空, 但不是从0变化到不空,由此poll线程通知其它poll线程if (c > 1) {headWaits.signal();}} finally {headLock.unlock();}// a. 从满->不满, 由此poll线程唤醒等待的offer线程if (c == array.length) {tailLock.lock();try {tailWaits.signal();} finally {tailLock.unlock();}}return e;}private boolean isEmpty() {return size.get() == 0;}private boolean isFull() {return size.get() == array.length;}}
最后
对各位小伙伴有帮助的话,希望可以点赞❤️+收藏⭐,谢谢各位大佬~~🙌🙌🙌


