( “树” 之 DFS) 437. 路径总和 III ——【Leetcode每日一题】

437. 路径总和 III

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

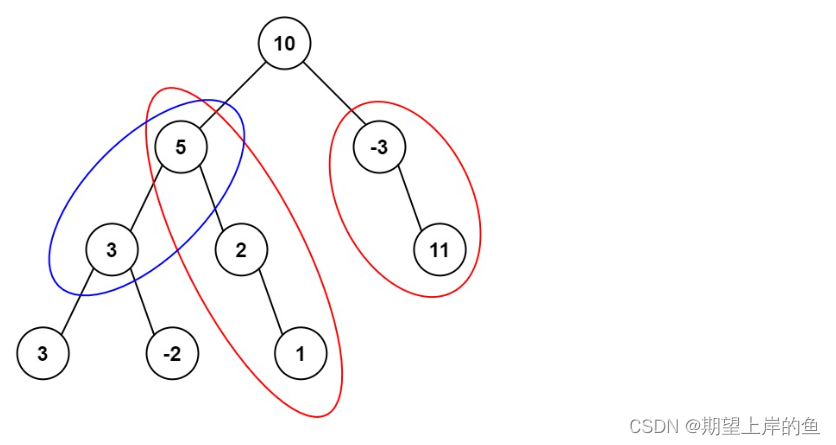
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

• 二叉树的节点个数的范围是 [0,1000]
• −109<=Node.val<=109-10^9 <= Node.val <= 10^9−109<=Node.val<=109
• $-1000<=targetSum<=1000$

思路：递归

我们首先想到的是路径不一定以 root 开头，也不一定以 leaf 结尾，但是必须连续。

• 所以在root节点有两类走法：路径不包含root，路径包含root：
  • 路径不包含root，targetSum不变，再从root的左右子树出发，调用pathSum；
  • 包含root，则判断当前节点的val是否等于targetSum，相等则路径加1，如果包含了，则左右子树也要一直包含。
• 一直递归，便可计算所有路径。

注意： 调用递归的时候传入的参数是targetSum - root.val，这里root.val太大了，递归调用多了targetSum-root.val就会溢出整数型的最小值。把参数类型换成long即可。

代码：(Java、C++)

Java

/* Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int pathSum(TreeNode root, int targetSum) {if(root == null) return 0;int ret = pathSumStartWithRoot(root, targetSum) + pathSum(root.left, targetSum) + pathSum(root.right, targetSum);return ret;}public int pathSumStartWithRoot(TreeNode root, long targetSum) {if(root == null) return 0;int ret = 0;if(targetSum == root.val){ret++;}ret += pathSumStartWithRoot(root.left, targetSum - root.val) + pathSumStartWithRoot(root.right, targetSum - root.val);return ret;}
}

C++

/* Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int pathSum(TreeNode* root, int targetSum) {if(root == NULL) return 0;int ret = pathSumStartWithRoot(root, targetSum) + pathSum(root->left, targetSum) + pathSum(root->right, targetSum);return ret;}int pathSumStartWithRoot(TreeNode* root, long targetSum) {if(root == NULL) return 0;int ret = 0;if(targetSum == root->val){ret++;}ret += pathSumStartWithRoot(root->left, targetSum - root->val) + pathSumStartWithRoot(root->right, targetSum - root->val);return ret;}
};

运行结果：

复杂度分析：

• 时间复杂度：O(n2)O(n^2 )O(n2)，其中 n 为该二叉树节点的个数。对于每一个节点，求以该节点为起点的路径数目时，则需要遍历以该节点为根节点的子树的所有节点，因此求该路径所花费的最大时间为 $O(n)$，我们会对每个节点都求一次以该节点为起点的路径数目，因此时间复杂度为 O(n2)O(n^2 )O(n2)。

• 空间复杂度： $O(n)$，考虑到递归需要在栈上开辟空间。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我 leetCode专栏，每日更新！

注： 如有不足，欢迎指正！