【图形学数学基础】矢量

数学基础(二)
-
- 矢量
-
- 零矢量
- 法线
- 矢量点积
- 矢量的叉积
只介绍一些重要些的基本概念,作为复习。
矢量
Vector 是构成2D,3D数学的正式数学单元,在数学中称为向量,在几何物理中称为矢量
矢量包含大小和方向。矢量的大小指矢量的长度,矢量可以具有任意非负长度。矢量的方向描述矢量在空间中所指方向。
矢量并没有位置,可以选择在任何地方的图形上表示它们。
矢量表示了一种位移,并且是相对位移
零矢量
零矢量表示为0,其并未任何方向和长度,表示一种无位移的状态。
法线
通常指的是垂直某物的矢量,由于垂直不需要长度,所以常用单位矢量。
矢量点积
两个矢量的点积是相应的分量乘积之和,得到的是一个标量
a⋅b=axbx+ayby(a,b为二维矢量)a⋅b=axbx+ayby+azbz(a,b为三维矢量)\\textbf{a} \\cdot \\textbf{b} = a_xb_x+a_yb_y (a,b 为二维矢量) \\\\ \\textbf{a} \\cdot \\textbf{b} = a_xb_x+a_yb_y +a_zb_z(a,b 为三维矢量) a⋅b=axbx+ayby(a,b为二维矢量)a⋅b=axbx+ayby+azbz(a,b为三维矢量)
点积可以给出两个矢量的大致方向,如果点积大于0则在同侧,等于零垂直,小于0夹角大于90度
点积的结合律,在一定程度上说明了投影的长度:
(ka)⋅b=k(a⋅b)=a⋅(kb)(k\\textbf{a})\\cdot \\textbf{b} = k(\\textbf{a}\\cdot \\textbf{b}) = \\textbf{a}\\cdot (k\\textbf{b}) (ka)⋅b=k(a⋅b)=a⋅(kb)
缩放a对b投影到a长度无影响。
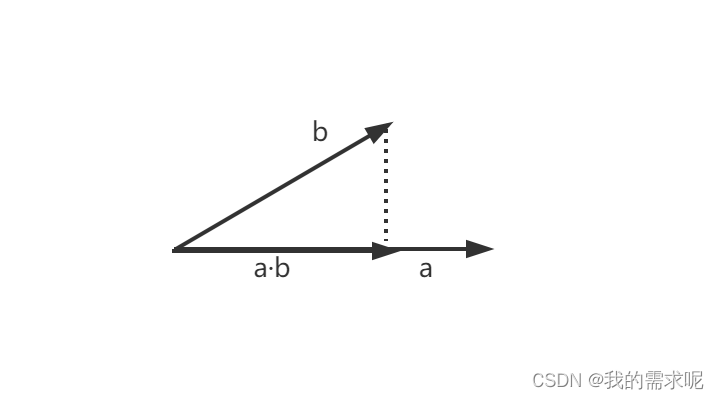
点积具有下面的几何属性:
- 点积a⋅b\\textbf{a} \\cdot \\textbf{b}a⋅b 相当于b\\textbf{b}b投影到a\\textbf{a}a上的长度值 再乘a\\textbf{a}a的长度
- 点积用来测量特定方向上的位移
- 投影运算和余弦函数密切相关。点积a⋅b\\textbf{a} \\cdot \\textbf{b}a⋅b也等于∥a∥∥b∥cosθ\\|\\textbf{a}\\| \\|\\textbf{b}\\| cos\\theta∥a∥∥b∥cosθ,其中,θ\\thetaθ是矢量间的角度
矢量的叉积
与点积不同,叉积只能在三维中使用,并且顺序是不可交换的,叉积产生的结果是矢量。
[x1y1z1]×[x2y2z2]=[y1z2−z1y2z1x2−x1z2x1y2−y1x2]\\left[ \\begin{array}{c} x_1 \\\\ y_1 \\\\ z_1 \\end{array} \\right ] \\times \\left[ \\begin{array}{c} x_2 \\\\ y_2 \\\\ z_2 \\end{array} \\right ] = \\left[ \\begin{array}{c} y_1z_2 - z_1y_2 \\\\ z_1x_2-x_1z_2 \\\\ x_1y_2-y_1x_2 \\end{array} \\right ] x1y1z1×x2y2z2=y1z2−z1y2z1x2−x1z2x1y2−y1x2
叉积和点积具有相同的运算优先级,但是当一起使用时叉积有限,因为其结果还是个矢量。
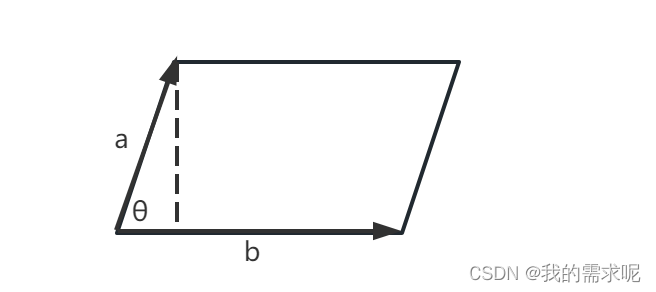
∥a×b∥=∥a∥∥b∥sinθ\\| a \\times b \\| = \\| a\\|\\|b\\| sin\\theta ∥a×b∥=∥a∥∥b∥sinθ
叉积的几何解释相当于,结果为a\\textbf{a}a和b\\textbf{b}b组成的平行四边形的面积