0.寻找峰值

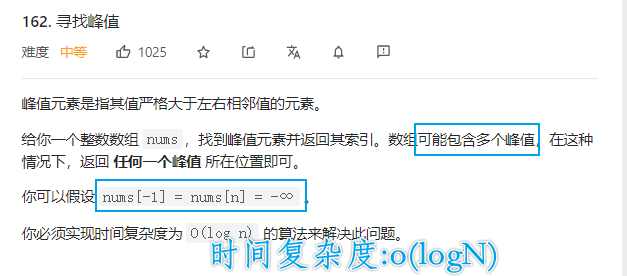
关键点:

• 返回任意一个峰值的下标即可
• nums[-1]=nums[n]=负无穷

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2

1.傻瓜编程(纯属玩乐)

class Solution {
public:int findPeakElement(vector<int>& a) {int n=a.size();if(n==1){return 0;}if(n==2){if(a[0]>a[1]){return 0;}else{return 1;}}for(int i=1;i<n-1;i++){if(a[0]>a[1]) return 0;if(a[n-2]<a[n-1]) return n-1;if(a[i]>a[i-1]&&a[i]>a[i+1]) return i;}return -1;}
};

2.二分

看到题目要求的时间复杂度是o(logN)，优先考虑二分查找，但是二分查找的前提似乎要是有序的，其实通过这题我们也能发现，使用二分法不一定要求有序，只要求可以确定答案一定会出现在其中一边即可

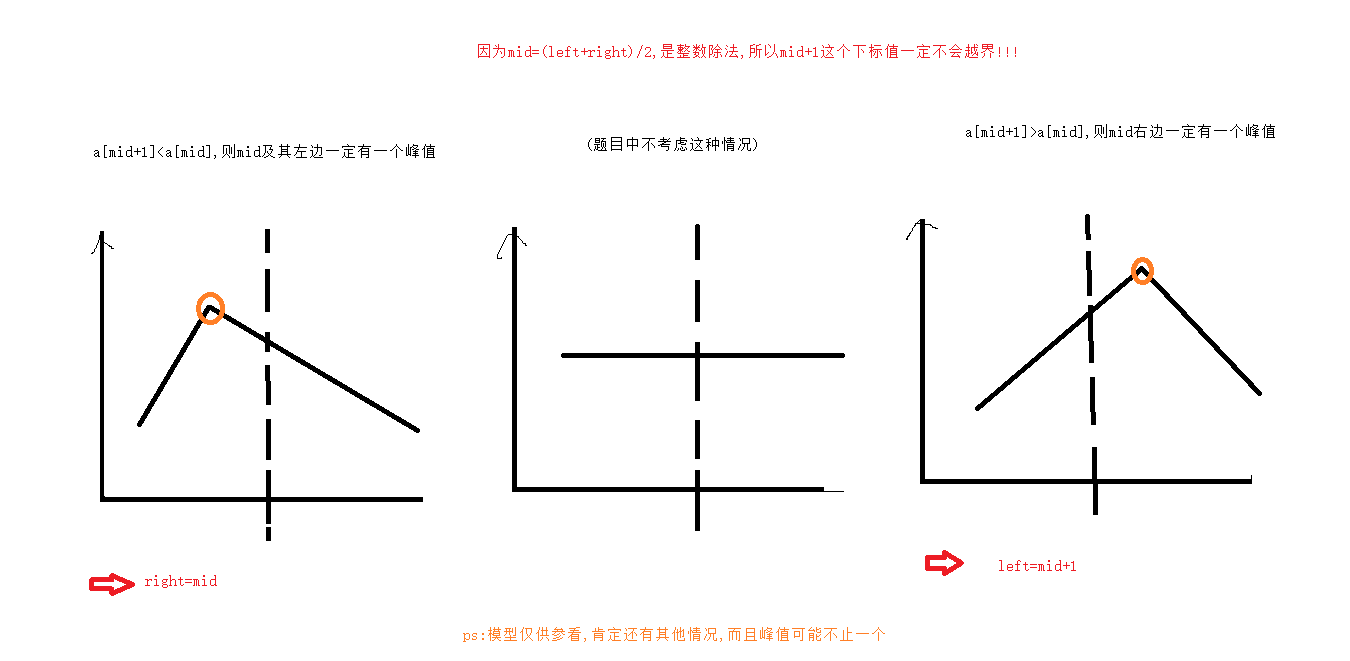
int findPeakElement(int* nums, int numsSize){int left=0,right=numsSize-1;while(left<right)//{int mid=left+(right-left)/2;if(nums[mid+1]>=nums[mid]){left=mid+1;//}else if(nums[mid+1]<nums[mid]){right=mid;//}}return left;
}

关键点：

• 因为mid=(left+right)/2这整数除法的特性，向下取整，只要数组元素个数大于等于2，mid+1下标一定存在（当数组元素等于1的时候，left==right,不会进该循环) , 而mid-1下标不一定存在，mid-1>=0减少边界讨论的情况
• 注意[left,right] 的范围就是答案所在的区域范围
• 最后left==right时定位到峰值的位置

蜜蜂养殖技术