牛顿法、梯度下降法与拟牛顿法

牛顿法、梯度下降法与拟牛顿法
- 0 引言
- 1 关于泰勒展开式
-
- 1.1 原理
- 1.2 例子
- 2 牛顿法
-
- 2.1 x 为一维
- 2.2 x 为多维
- 3 梯度下降法
- 4 拟牛顿法
-
- 4.1 拟牛顿条件
- 4.2 DFP 算法
- 4.3 BFGS 算法
- 4.4 L-BFGS 算法
0 引言
机器学习中在求解非线性优化问题时,常用的是梯度下降法和拟牛顿法,梯度下降法和拟牛顿法都是牛顿法的一种简化
牛顿法是在一个初始极小值点做二阶泰勒展开,然后对二阶泰勒展开式求极值点,通过迭代的方式逼近原函数极值点
在牛顿法迭代公式中,需要求二阶导数,而梯度下降法将二阶导数简化为一个固定正数方便求解
拟牛顿法也是在求解过程中做了一些简化,不用直接求二阶导数矩阵和它的逆
1 关于泰勒展开式
1.1 原理
如果我们有一个复杂函数 f(x)f(x)f(x), 对这个复杂函数我们想使用 n 次多项式(多项式具有好计算,易求导,且好积分等一系列的优良性质)去拟合这个函数,这时就可以对 f(x)f(x)f(x)进行泰勒展开,求某一点 x0x_0x0附近的 n 次多项式:
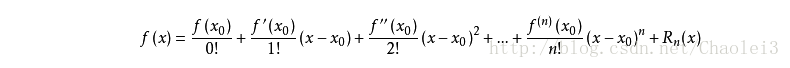
注意:
n 次多项式只是在 x0x_0x0 较小的邻域内能较好拟合 f(x)f(x)f(x),也就是说,泰勒展开式其实是一种局部近似的方法,只近似 x=x0x=x_0x=x0那一点的函数性
1.2 例子
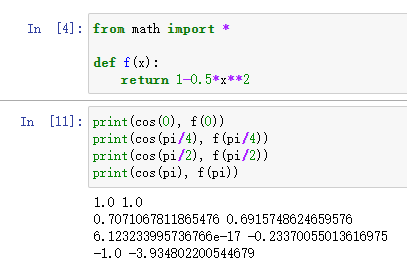
现在要求 f(x)=cos(x)f(x)=cos(x)f(x)=cos(x) 在 x0=0x_0=0x0=0 处的二阶泰勒展开,因为我们去掉了高阶项,所以只是近似
直接套用公式
f(x0)=f(0)=cos(0)=1f(x_0)=f(0)=cos(0)=1f(x0)=f(0)=cos(0)=1
f′(x0)=f′(0)=−sin(0)=0f'(x_0)=f'(0)=-sin(0)=0f′(x0)=f′(0)=−sin(0)=0
f′′(x0)=f′′(0)=−cos(0)=−1f''(x_0)=f''(0)=-cos(0)=-1f′′(x0)=f′′(0)=−cos(0)=−1
所以展开后的公式为
f(x)≈f(x0)+f′(x0)∗x+f′′(x0)∗x2/2=1−0.5∗x2f(x)≈f(x_0)+f'(x_0)*x+f''(x_0)*x^2/2=1-0.5*x^2f(x)≈f(x0)+f′(x0)∗x+f′′(x0)∗x2/2=1−0.5∗x2
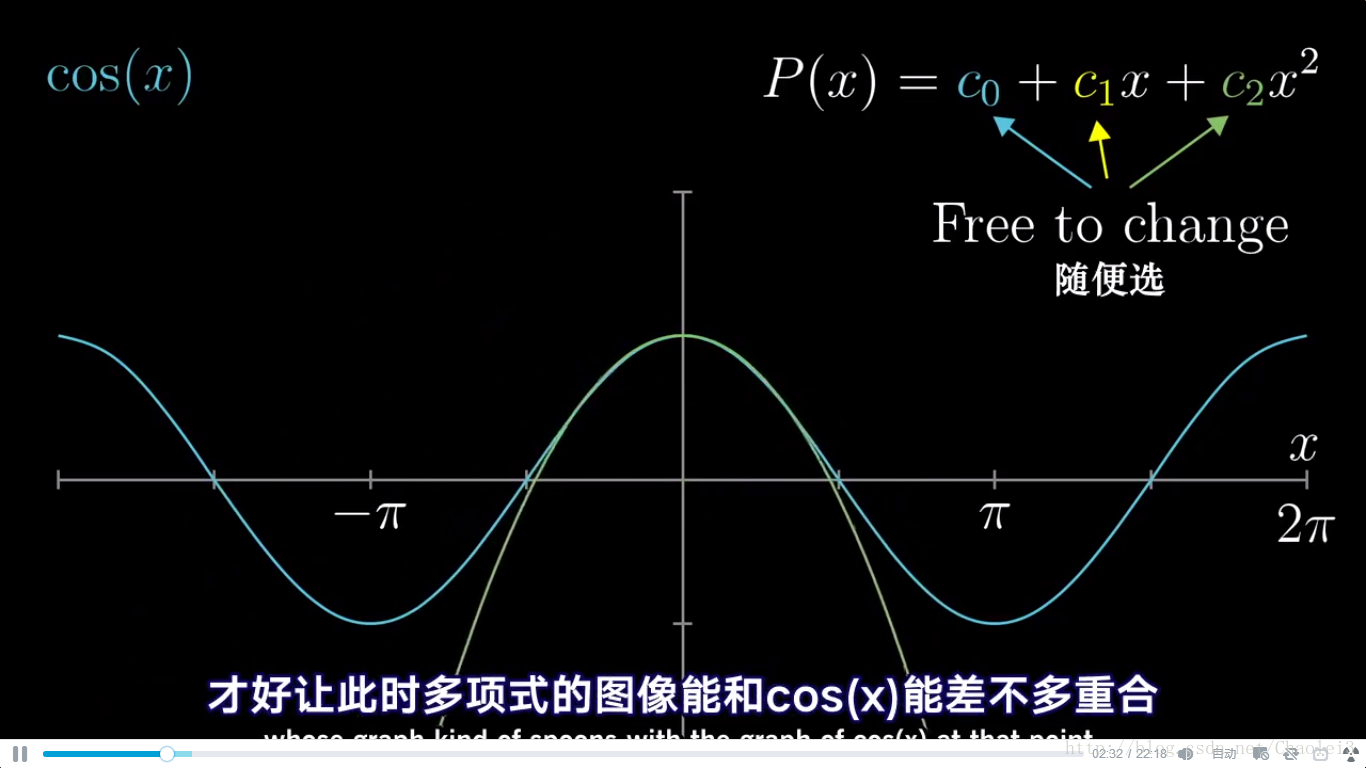
从下方运行程序可以看出,离展开点越近的点,拟合程度越高,越远的点,越离谱
2 牛顿法
2.1 x 为一维
现在假设我们有目标函数 f(x)f(x)f(x),我们希望求此函数的极小值,牛顿法的基本思想是:随机找到一个点设为当前极值点 xkx_kxk,在这个点对 f(x)f(x)f(x) 做二次泰勒展开,进而找到极小点的下一个估计值。在 xkx_kxk 附近的二阶泰勒展开为:
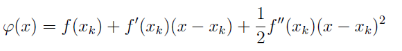
现在想求 φ(x)\\varphi(x)φ(x) 的极值点,由极值的必要条件可知,φ(x)\\varphi(x)φ(x) 应满足导数为 0,即:
φ′(x)=0\\varphi'(x)=0 φ′(x)=0
即
φ′(x)=f′(xk)+f′′(xk)(x−xk)=0\\varphi'(x)=f'(x_k)+f''(x_k)(x-x_k)=0 φ′(x)=f′(xk)+f′′(xk)(x−xk)=0
这样就可以求得 x 的值
x=xk−f′(xk)f′′(xk)x=x_k-\\frac{f'(x_k)}{f''(x_k)}x=xk−f′′(xk)f′(xk)
于是给定初始值 x0x_0x0,就可以通过迭代的方式逼近f(x)f(x)f(x)的极值点:
xk+1=xk−f′(xk)f′′(xk)x_{k+1}=x_k-\\frac{f'(x_k)}{f''(x_k)}xk+1=xk−f′′(xk)f′(xk)
如下图,首先在 xnx_nxn 处泰勒展开,得到f(x)f(x)f(x) 的近似函数 gn(x)g_n(x)gn(x) ,求得 gn(x)g_n(x)gn(x) 的极值点 xn+1x_{n+1}xn+1
随后在 xn+1x_{n+1}xn+1 出泰勒展开,得到gn+1(x)g_{n+1}(x)gn+1(x) 函数,继续求gn+1(x)g_{n+1}(x)gn+1(x) 的极值点
一直迭代最后就会逼近 f(x)f(x)f(x) 的极值点

2.2 x 为多维
上面讨论的是参数 x 为一维的情况,当 x 有多维时,二阶泰勒展开式可以做推广,此时:
φ(x)=f(xk)+∇f(xk)∗(x−xk)+12∗(x−xk)T∗∇2f(xk)∗(x−xk)\\varphi(x)=f(x_k)+\\nabla{f(x_k)}*(x-x_k)+ \\frac{1}{2}*(x-x_k)^T*\\nabla^2{f(x_k)}*(x-x_k)φ(x)=f(xk)+∇f(xk)∗(x−xk)+21∗(x−xk)T∗∇2f(xk)∗(x−xk)
其中 ∇f\\nabla{f}∇f为 fff 的梯度向量,∇2f\\nabla^2{f}∇2f为 fff的海森矩阵(Hessian matrix),其定义为:
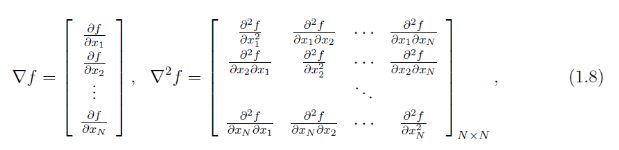
φ(x)\\varphi(x)φ(x)对 x 向量求导并令其为 0 有:
∇f(xk)+∇2f(xk)∗(x−xk)=0\\nabla{f(x_k)}+\\nabla^2{f(x_k)}*(x-x_k)=0∇f(xk)+∇2f(xk)∗(x−xk)=0
于是有:
x=xk−[∇2f(xk)]−1∇f(xk)x=x_k-[\\nabla^2{f(x_k)}]^{-1}\\nabla{f(x_k)}x=xk−[∇2f(xk)]−1∇f(xk)
通过迭代的方式能找到函数的极值点
牛顿法缺点:
- 函数必须具有一二阶偏导数,海森矩阵必须正定
- 计算相当复杂,除梯度外还需要计算二阶偏导数和逆矩阵
3 梯度下降法
在一维牛顿法中,迭代公式为:
xk+1=xk−f′(xk)f′′(xk)x_{k+1}=x_k-\\frac{f'(x_k)}{f''(x_k)}xk+1=xk−f′′(xk)f′(xk)
这个公式缺点:
- 需要求二阶导数,有些函数求二阶导数之后就相当复杂了;
- 因为f′′(xn)f''(x_n)f′′(xn)的大小不定,所以g(x)g(x)g(x)开口方向不定,我们无法确定最后得到的结果究竟是极大值还是极小值
为了解决这两个问题,我们放弃二阶精度,即去掉f′′(xn)f''(x_n)f′′(xn),改为一个固定的正数1/h:
φ(x)=f(xk)+f′(xk)(x−xk)+12h(x−xk)2\\varphi(x)=f(x_k)+f'(x_k)(x-x_k)+\\frac{1}{2h}(x-x_k)^2 φ(x)=f(xk)+f′(xk)(x−xk)+2h1(x−xk)2
该抛物线是一条开口向上的抛物线,通过求它的极值可以保证得到的是极小值。φ(x)\\varphi(x)φ(x) 的极小值点为
xk−hf′(xk)x_k-hf'(x_k)xk−hf′(xk)
迭代公式为
xk+1=xk−hf′(xk)x_{k+1} = x_k-hf'(x_k)xk+1=xk−hf′(xk)
对于高维空间就是
xk+1=xk−h∇(xk)x_{k+1} = x_k-h\\nabla(x_k)xk+1=xk−h∇(xk)
4 拟牛顿法
拟牛顿法的基本思想是:不用二阶偏导数而构造出可以近似海森矩阵的正定对称阵,在“拟牛顿”的条件下优化目标函数。不同的构造方法就产生了不同的拟牛顿法。
一些记号:
∇f\\nabla{f}∇f 记为 g 表示梯度, gkg_kgk表示∇f(xk)\\nabla{f(x_k)}∇f(xk)
∇2f\\nabla^2{f}∇2f 海森矩阵,记为 H, KkK_kKk表示∇2f(xk)\\nabla^2{f(x_k)}∇2f(xk)
用 B 表示对海森矩阵 H 本身的近似,D表示对海森矩阵的逆 H−1H^{-1}H−1的近似, 即 B≈H,D≈H−1B≈H, D≈H^{-1}B≈H,D≈H−1
4.1 拟牛顿条件
在经过 k+1 次迭代后得到 xk+1x_{k+1}xk+1,此时目标函数f(x)f(x)f(x)在 xk+1x_{k+1}xk+1处作泰勒二阶展开,得到:
f(x)≈f(xk+1)+∇f(xk+1)∗(x−xk+1)+12∗(x−xk+1)T∗∇2f(xk+1)∗(x−xk+1)f(x)≈f(x_{k+1})+\\nabla{f(x_{k+1})}*(x-x_{k+1})+ \\frac{1}{2}*(x-x_{k+1})^T*\\nabla^2{f(x_{k+1})}*(x-x_{k+1})f(x)≈f(xk+1)+∇f(xk+1)∗(x−xk+1)+21∗(x−xk+1)T∗∇2f(xk+1)∗(x−xk+1)
两边对 x 求梯度有:
∇f(x)≈∇f(xk+1)+Hk+1∗(x−xk+1)(1)\\nabla{f(x)} ≈ \\nabla{f(x_{k+1})}+H_{k+1}*(x-x_{k+1}) \\tag{1}∇f(x)≈∇f(xk+1)+Hk+1∗(x−xk+1)(1)
在式(1)中取 x=xkx=x_kx=xk ,整理可得:
gk+1−gk≈Hk+1∗(xk+1−xk)(2)g_{k+1}-g_{k}≈H_{k+1}*(x_{k+1}-x_k)\\tag{2}gk+1−gk≈Hk+1∗(xk+1−xk)(2)
引入记号:
sk=xk+1−xk,yk=gk+1−gks_k=x_{k+1}-x_k,y_k=g_{k+1}-g_{k}sk=xk+1−xk,yk=gk+1−gk
式 (2) 可以写为:
yk≈Hk+1∗sk=>简记为:yk≈Bk+1∗sky_k≈H_{k+1}*s_k =>简记为:y_k≈B_{k+1}*s_kyk≈Hk+1∗sk=>简记为:yk≈Bk+1∗sk
或者
sk≈Hk+1−1∗gk=>简记为:sk≈Dk+1∗yks_k≈H^{-1}_{k+1}*g_k=>简记为:s_k≈D_{k+1}*y_ksk≈Hk+1−1∗gk=>简记为:sk≈Dk+1∗yk
这就是所谓的拟牛顿条件,它对迭代过程中的海森矩阵做约束。
4.2 DFP 算法
参考:牛顿法与拟牛顿法学习笔记(三)DFP 算法
4.3 BFGS 算法
参考:牛顿法与拟牛顿法学习笔记(四)BFGS 算法
4.4 L-BFGS 算法
牛顿法与拟牛顿法学习笔记(五)L-BFGS 算法
参考:
泰勒展开式的理解
牛顿法与拟牛顿法学习笔记(一)牛顿法
梯度下降和EM算法:系出同源,一脉相承
Markdown公式、特殊字符、上下标、求和/积分、分式/根式、字体


