C#，码海拾贝（19）——一般实矩阵的QR分解（QR Decomposition）方法之C#源代码，《C#数值计算算法编程》源代码升级改进版

1 实矩阵

实矩阵，指的是矩阵中所有的数都是实数的矩阵。如果一个矩阵中含有除实数以外的数，那么这个矩阵就不是实矩阵。

2 QR（正交三角）分解法

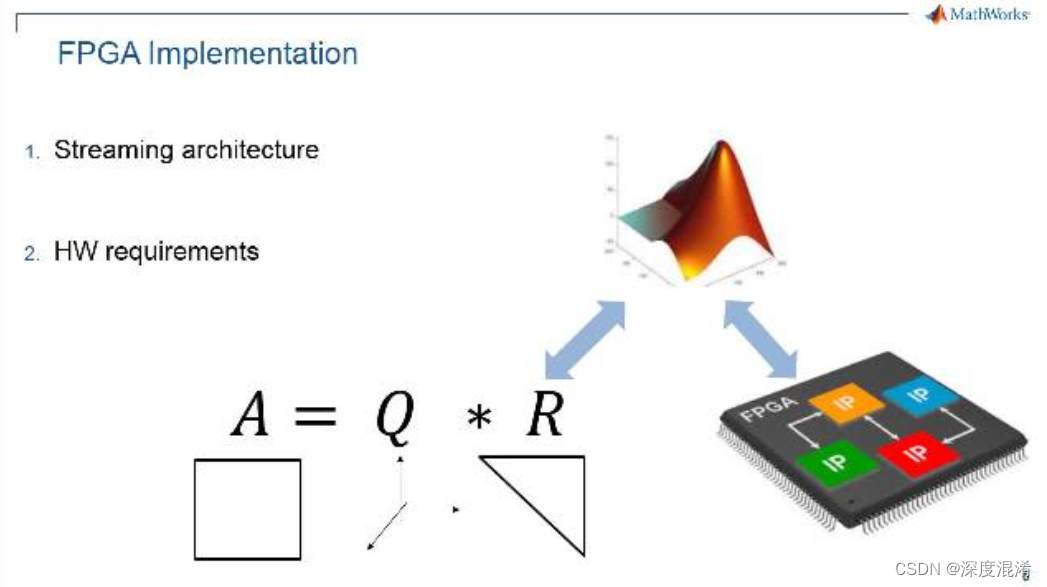
QR（正交三角）分解法是求一般矩阵全部特征值的最有效并广泛应用的方法，一般矩阵先经过正交相似变化成为Hessenberg矩阵，然后再应用QR方法求特征值和特征向量。它是将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R，所以称为QR分解法，与此正规正交矩阵的通用符号Q有关。
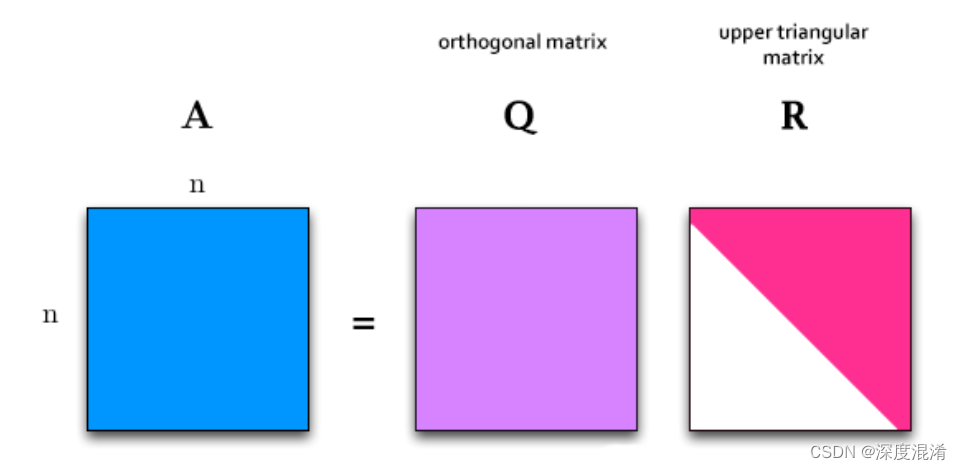
如果实（复）非奇异矩阵A能够化成正交（酉）矩阵Q与实（复）非奇异上三角矩阵R的乘积，即A=QR，则称其为A的QR分解。
矩阵的正交分解又称为QR分解，是将矩阵分解为一个正交矩阵Q和一个上三角矩阵的乘积的形式。
任意实数方阵A，都能被分解为。这里的Q为正交单位阵，即。R是一个上三角矩阵。这种分解被称为QR分解。

QR分解也有若干种算法，常见的包括Gram–Schmidt、Householder和Givens算法。

QR分解是将矩阵分解为一个正交矩阵与上三角矩阵的乘积。

3 分解流程

（1）对需要求解的特征值的矩阵进行QR分解
（2）对分解出来的结果进行逆向相乘
（3）将相乘得到的矩阵进行QR分解
（4）对分解出来的结果进行逆向相乘

4 实用意义

使用qr分解有助于加快解方程或求解速度即收敛速度。

5 应用领域

系统辨识是现代控制理论的重要组成部分。对系统的结构和参数进行辨识在工程上和理论上都占有重要的地位。最小二乘法是系统参数辨识中的重要估计方法,并在众多领域和场合得到了广泛的应用。
 

6 QR（正交三角）分解法C#源程序

using System;namespace Zhou.CSharp.Algorithm
{/// <summary>/// 矩阵类/// 作者：周长发/// 改进：深度混淆/// https://blog.csdn.net/beijinghorn/// </summary>public partial class Matrix{/// <summary>/// 一般实矩阵的QR分解，分解成功后，原矩阵将成为R矩阵/// </summary>/// <param name="src">源矩阵</param>/// <param name="mtxQ">分解后的Q矩阵</param>/// <returns>求解是否成功</returns>public static bool SplitQR(Matrix src, Matrix mtxQ){int i, j, k, z, nn, p, jj;double u, alpha, w, t;if (src.Rows < src.Columns){return false;}// 初始化Q矩阵if (!mtxQ.Init(src.Rows, src.Rows)){return false;}// 对角线元素单位化for (i = 0; i <= src.Rows - 1; i++){for (j = 0; j <= src.Rows - 1; j++){z = i * src.Rows + j;mtxQ[z] = 0.0;if (i == j){mtxQ[z] = 1.0;}}}// 开始分解nn = src.Columns;if (src.Rows == src.Columns){nn = src.Rows - 1;}for (k = 0; k <= nn - 1; k++){u = 0.0;z = k * src.Columns + k;for (i = k; i <= src.Rows - 1; i++){w = Math.Abs(src[i * src.Columns + k]);if (w > u){u = w;}}alpha = 0.0;for (i = k; i <= src.Rows - 1; i++){t = src[i * src.Columns + k] / u;alpha = alpha + t * t;}if (src[z] > 0.0){u = -u;}alpha = u * Math.Sqrt(alpha);if (Math.Abs(alpha) < float.Epsilon){return false;}u = Math.Sqrt(2.0 * alpha * (alpha - src[z]));if ((u + 1.0) != 1.0){src[z] = (src[z] - alpha) / u;for (i = k + 1; i <= src.Rows - 1; i++){p = i * src.Columns + k;src[p] = src[p] / u;}for (j = 0; j <= src.Rows - 1; j++){t = 0.0;for (jj = k; jj <= src.Rows - 1; jj++){t = t + src[jj * src.Columns + k] * mtxQ[jj * src.Rows + j];}for (i = k; i <= src.Rows - 1; i++){p = i * src.Rows + j;mtxQ[p] = mtxQ[p] - 2.0 * t * src[i * src.Columns + k];}}for (j = k + 1; j <= src.Columns - 1; j++){t = 0.0;for (jj = k; jj <= src.Rows - 1; jj++){t = t + src[jj * src.Columns + k] * src[jj * src.Columns + j];}for (i = k; i <= src.Rows - 1; i++){p = i * src.Columns + j;src[p] = src[p] - 2.0 * t * src[i * src.Columns + k];}}src[z] = alpha;for (i = k + 1; i <= src.Rows - 1; i++){src[i * src.Columns + k] = 0.0;}}}// 调整元素for (i = 0; i <= src.Rows - 2; i++){for (j = i + 1; j <= src.Rows - 1; j++){p = i * src.Rows + j;z = j * src.Rows + i;t = mtxQ[p];mtxQ[p] = mtxQ[z];mtxQ[z] = t;}}return true;}}
}

POWER BY 315SOFT.COM

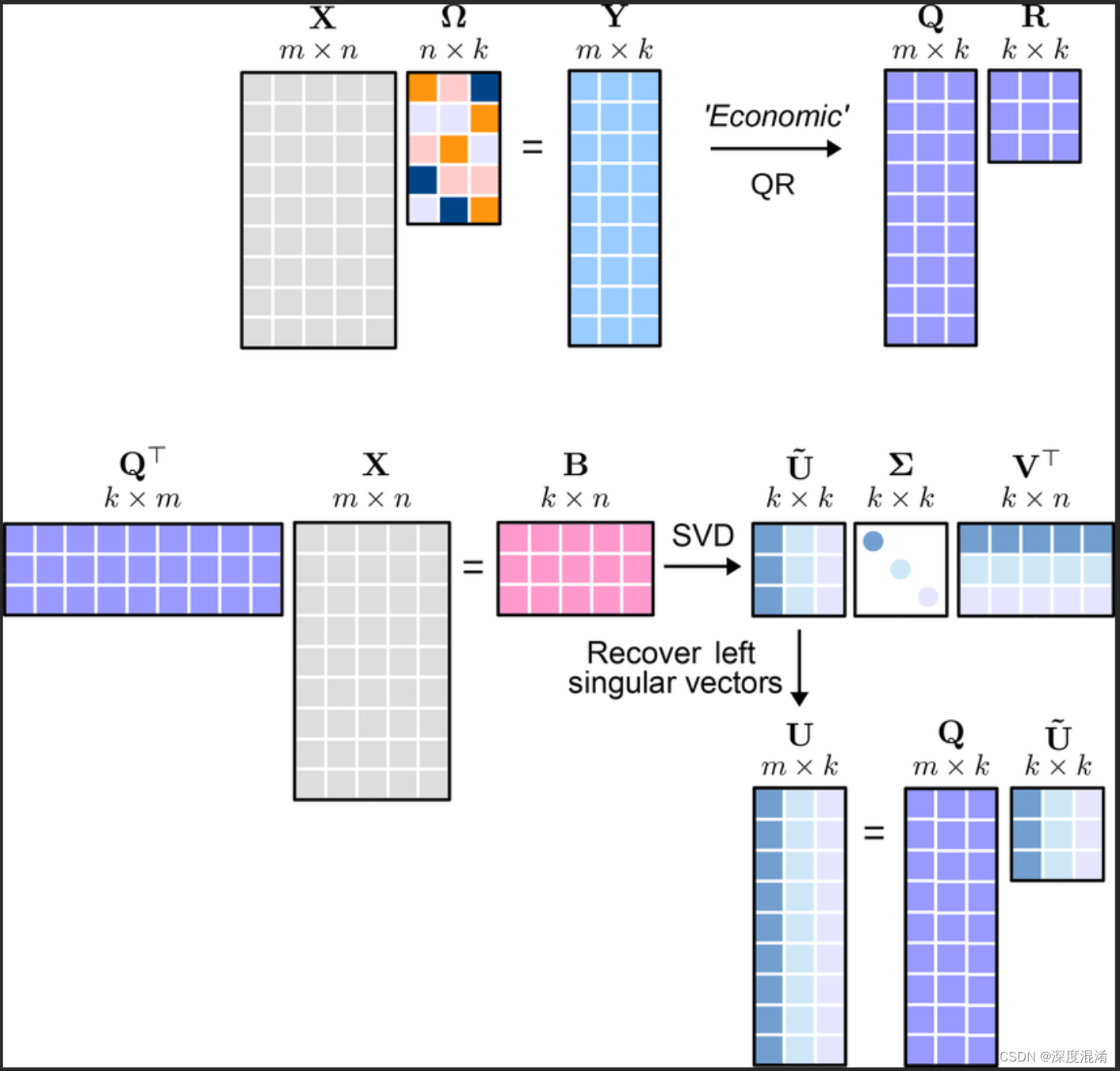
The QR decomposition (or QR factorization) allows us to express a matrix having linearly independent columns as the product of 1) a matrix Q having orthonormal columns and 2) an upper triangular matrix R.