排序算法总结

sort
绝大多数时候,我们直接使用头文件 中的 sort 函数对数组进行排序。
#include <cstdio>
#include <algorithm>
const int N = 1007;
int a[N];
int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; ++i)scanf("%d", a + i);//默认从小到大排序,第一个参数是待排序中第一个元素的地址,第二个参数是最后一个元素的地址的下一个位置std::sort(a+1, a+n+1);for (int i = 1; i <= n; ++i)printf("%d ", a[i]);return 0;
}
/*
输入:
5
3 7 1 0 4
输出:
0 1 3 4 7
*/
要改成从大到小排序,需要加一个头文件和一个参数:
#include <cstdio>
#include <functional>
#include <algorithm>
const int N = 1007;
int a[N];
int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; ++i)scanf("%d", a + i);//默认从小到大排序,第一个参数是待排序中第一个元素的地址,第二个参数是最后一个元素的地址的下一个位置std::sort(a+1, a+n+1, std::greater<int>());for (int i = 1; i <= n; ++i)printf("%d ", a[i]);return 0;
}
/*
输入:
5
3 7 1 0 4
输出:
7 4 3 1 0
*/
我们也可以单独使用一个比较函数 cmp 来进行排序,例如,我们要对 n 个数进行如下规则的排序:
-
所有的奇数排在前面,所有的偶数排在后面;
-
奇数按从小到大排序,偶数按从大到小排序。
#include <cstdio>
#include <algorithm>
const int N = 1007;
int a[N];
bool cmp(const int &a, const int &b) { if (a%2==1 && b%2==0) return true;if (a%2==1 && b%2==1 && a<b) return true;if (a%2==0 && b%2==0 && a>b) return true;return false;
}int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; ++i)scanf("%d", a + i);//第三个参数为比较函数名std::sort(a+1, a+n+1, cmp);for (int i = 1; i <= n; ++i)printf("%d ", a[i]);return 0;
}
/*
输入:
10
1 2 3 4 5 6 7 8 9 10
输出:
1 3 5 7 9 10 8 6 4 2
*/
注意:sort 采用快速排序算法,不是稳定的排序算法
排序的稳定性
如果数组中有 2 个元素的数值相同,排序后这 2 个元素的前后顺序保持不变,则我们称这样的排序是稳定的。
选择排序(不稳定)
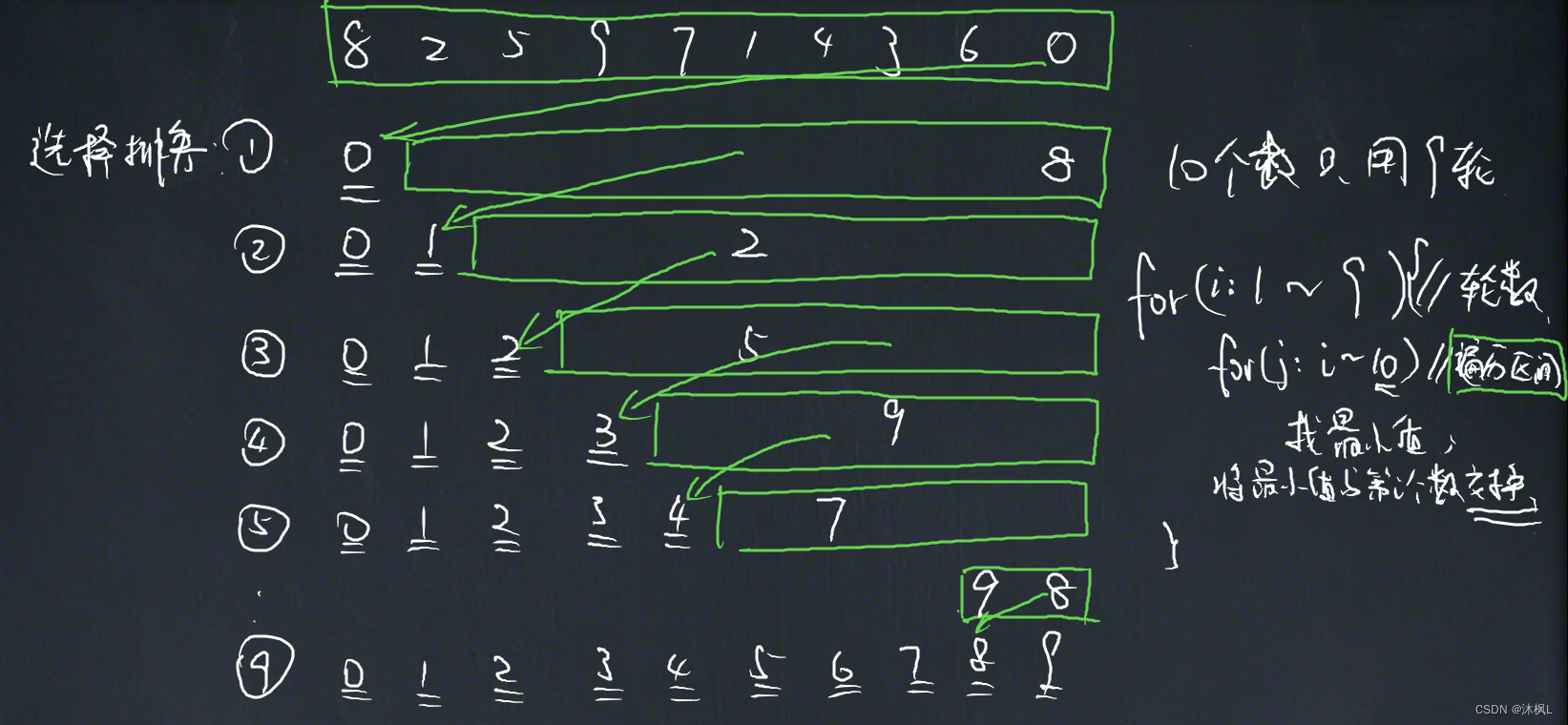
时间复杂度:
最好:O(n2)O(n^2)O(n2),最坏:O(n2)O(n^2)O(n2)
//C语言版
#include <stdio.h>
int a[607];
int main(){int n, i, id, j, t;scanf("%d", &n);for (i = 1; i <= n; ++i) scanf("%d", &a[i]);//选择排序for (i = 1; i < n; ++i) {id = i;for (j = i + 1; j <= n; ++j)if (a[j] < a[id]) id = j;//交换a[id] 和 a[i] if (id != i) t = a[id], a[id] = a[i], a[i] = t;}printf("%d %d %d", a[1], a[2], a[3]);return 0;
}
#include <cstdio>
#include <algorithm>
int a[107];
void select_sort(int a[], int n) {//a并非数组,而是一个指针,指向数组首地址//该函数内的a与全局变量a数组是两个不同的变量for (int i = 1; i < n; ++i) {int id = i;for (int j = i + 1; j <= n; ++j)if (a[j] < a[id]) id = j;if (id != i) std::swap(a[i], a[id]);}
}
int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", a + i);select_sort(a, n);for (int i = 1; i <= n; ++i) printf("%d ", a[i]);return 0;
}
/*
输入:
10
8 2 5 9 7 1 3 4 6 0
输出:
0 1 2 3 4 5 6 7 8 9
*/
选择排序不稳定的原因:
看如下的一个例子:
(Jason, 287), (Ada, 200), (Mike, 287), (Cindy, 100)
第一步选出最小值 (Cindy, 100),数组变为 (Cindy, 100), (Ada, 200), (Mike, 287), (Jason, 287)
排序完成,两个287分的同学,相对位置发生了变化。
由于在排序中,无法保证相等的两个元素相对位置不变,我们称选择排序为不稳定的排序。
插入排序(稳定)
插入排序的算法思想源于扑克牌游戏。



时间复杂度:
最好:O(n)O(n)O(n),最坏:O(n2)O(n^2)O(n2)
#include <stdio.h>
int a[607];
int main(){int n, i, id, j, k;scanf("%d", &n);for (i = 1; i <= n; ++i) scanf("%d", &a[i]);//插入排序for (i = 2; i <= n; ++i) {//把大于a[i]的数都往后挪for (j=i-1, k=a[i]; j && a[j]>k; --j)a[j+1] = a[j];a[j+1] = k;}printf("%d %d %d", a[1], a[2], a[3]);return 0;
}
#include <cstdio>
int a[107];
void insert_sort(int a[], int n) {for (int i = 2, j, t; i <= n; ++i) {for (j = i-1, t = a[i]; j && t<a[j]; --j)a[j+1] = a[j];a[j+1] = t;}
}
int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", a + i);insert_sort(a, n);for (int i = 1; i <= n; ++i) printf("%d ", a[i]);return 0;
}
冒泡排序(稳定)

时间复杂度:
最好:O(n2)O(n^2)O(n2),最坏:O(n2)O(n^2)O(n2)
#include <stdio.h>
int a[607];
int main(){int n, i, j, t;scanf("%d", &n);for (i = 1; i <= n; ++i) scanf("%d", &a[i]);//冒泡排序for (i = n-1; i; --i) {for (j = 1; j <= i; ++j)if (a[j] > a[j+1])t = a[j], a[j] = a[j+1], a[j+1] = t;}printf("%d %d %d", a[1], a[2], a[3]);return 0;
}
注意:若某一轮未发生交换,则说明已完成排序。
时间复杂度:
最好:O(n)O(n)O(n),最坏:O(n2)O(n^2)O(n2)
#include <stdio.h>
#define swap(a,b,t) {t=a,a=b,b=t;}
int a[607];
int main(){int n, i, j, t, flag;scanf("%d", &n);for (i = 1; i <= n; ++i) scanf("%d", &a[i]);for (i = n-1; i; --i) {flag = 1;for (j = 1; j <= i; ++j)if (a[j] > a[j+1]) {swap(a[j], a[j+1], t)flag = 0;}if (flag) break;}printf("%d %d %d", a[1], a[2], a[3]);return 0;
}
#include <cstdio>
inline void swap(int &a, int &b) { int t = a; a = b; b = t; }
int a[107];
void bubble_sort(int a[], int n) {for (int i = n-1; i; --i) {int cnt = 0;//cnt为本轮逆序对数for (int j = 1; j <= i; ++j)if (a[j] > a[j+1]) swap(a[j], a[j+1]), ++cnt;if (!cnt) break;}
}
int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", a + i);bubble_sort(a, n);for (int i = 1; i <= n; ++i) printf("%d ", a[i]);return 0;
}
计数排序(稳定)

#include <cstdio>
//N 为个数,M 为取值范围[0, M]
//M<=kN,即 N 的整数倍,速度最快,最好是 N 远大于 M;
const int N = 107, M = 1e3 + 7;
int a[N], c[M], ans[N];
void count_sort(int a[], int n) {for (int i = 1; i <= n; ++i) ++c[a[i]];for (int i = 1; i < M; ++i)c[i] += c[i-1];for (int i = n; i; --i)ans[c[a[i]]--] = a[i];
}
int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; ++i)scanf("%d", a + i);count_sort(a, n);for (int i = 1; i <= n; ++i)printf("%d ", ans[i]);return 0;
}
基数排序(稳定)
// int 范围内的非负整数排序
#include <iostream>
#include <cstring>
const int N = 1e5 + 7;
int a[N], c[260], n, b[N];
void rsort() {for (int k = 0; k < 32; k += 8) {memset(c, 0, sizeof c);for (int i = 1; i <= n; ++i) ++c[a[i]>>k & 0xFF];for (int i = 1; i <= 0xFF; ++i) c[i] += c[i-1];for (int i = n; i; --i) {int t = a[i]>>k & 0xFF;b[c[t]--] = a[i];}for (int i = 1; i <= n; ++i) a[i] = b[i];}
}
int main() {scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", a + i);rsort();for (int i = 1; i <= n; ++i) printf("%d ", a[i]);puts("");return 0;
}
桶排序
普通情况的单值排序,只要取值范围不大于元素个数,就可以使用桶排序。每个元素的值对应一个桶,桶里存放一个数:
true(对应这个值在数组中存在),false(对应这个值不在数组中)- 一个整数,表示这个数在数组中出现的次数。
例1:给 7 1 9 2 3 排序。
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| a[i] | 7 | 1 | 9 | 2 | 3 |
用 bucket 的首字母 b 作为桶数组的名称。
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| b[i] | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
上面如同 101010 个桶,编号分别为 0∼90\\sim 90∼9,如果我们只记录每个数是否出现,则 bbb 数组可使用 bool 类型;如果要记录每个数出现的次数, bbb 数组就需要用 int 类型。
要输出排序结果,只需要从 0∼90\\sim 90∼9 依次检查每个桶是否为 111,如果为 111 就输出对应的桶的编号 iii。
该算法时间复杂度为 O(n+m)O(n+m)O(n+m),nnn 为元素个数,mmm 为取值范围,如果 m≈nm\\approx nm≈n,那么该算法的时间复杂度为 O(n)O(n)O(n),即可实现线性时间排序。
例2:输出 1 2 1 2 1 排序后的结果,重复数字不需要输出。
方法同上一个例子。
#include <iostream>
using namespace std;
const int N = 107;
int a[N];
bool b[N];
int main() {int n;scanf("%d", &n);for (int i = 1, x; i <= n; ++i) {scanf("%d", &x);b[x] = true;}// 注意对桶的循环范围for (int i = 0; i < 10; ++i)if (b[i]) printf("%d ", i);
}例3:输出 1 2 1 2 1 排序后的结果。
如果排序后多数字需要多次输出,则我们必须在桶里给每个数计数。
#include <iostream>
using namespace std;
const int N = 107;
int a[N], b[N];
int main() {int n;scanf("%d", &n);for (int i = 1, x; i <= n; ++i) {scanf("%d", &x);++b[x];}// 注意对桶的循环范围for (int i = 0; i < 10; ++i)for (int j = 1; j <= b[i]; ++j) printf("%d ", i);
}那么,当排序的数字有小数怎么办呢?这个时候就需要二维数组来存放了。
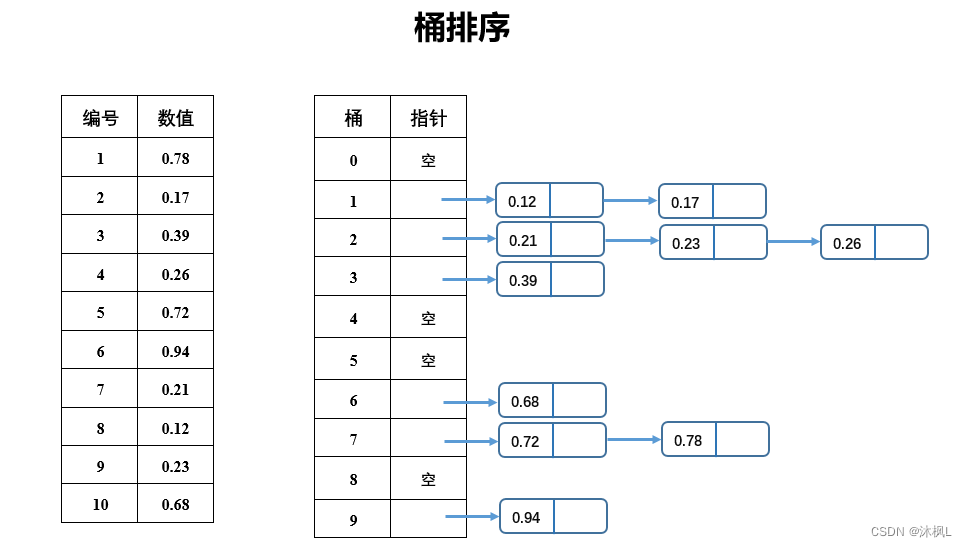
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 107;
double a[N], f[N][N];
void buck_sort(double a[], int n) {for (int i = 1, j; i <= n; ++i) {int u = int(a[i] * 10) % 10;for (j = f[u][0]++; j && f[u][j]>a[i]; --j)f[u][j+1] = f[u][j];f[u][j+1] = a[i];}
}
int main() {freopen("1.in", "r", stdin);int n;scanf("%d", &n);for (int i = 1, j; i <= n; ++i)scanf("%lf", a + i);buck_sort(a, n);for (int i = 0; i <= 9; ++i)for (int j = 1; j <= f[i][0]; ++j)printf("%.2f ", f[i][j]);return 0;
}
归并排序(稳定)

#include <iostream>
typedef long long LL;
const int N = 1e5 + 7;
int a[N], b[N];
LL msort(int lo, int hi) {if (lo == hi) return 0;int mid = (lo + hi) >> 1;//ans记录逆序对的个数LL ans = msort(lo, mid) + msort(mid+1, hi);//i合并后的新编号,j左半边的编号,k右半边的编号for (int i=lo, j=lo, k=mid+1; i <= hi; ++i) {if (j > mid) { b[i] = a[k++]; continue; }if (k > hi) { b[i] = a[j++]; continue; }if (a[j] <= a[k]) { b[i] = a[j++]; continue; }ans += mid - j + 1, b[i] = a[k++];}for (int i = lo; i <= hi; ++i) a[i] = b[i];return ans;
}
int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", a + i);LL ans = msort(1, n);printf("%lld", ans);return 0;
}
堆排序(heap_sort(int c[], int n))
#include <iostream>
#include <algorithm>
const int N = 107;
int c[N], n;
void adjust(int cur, int n) {int x = c[cur], chd = cur << 1;while (chd <= n) {if (chd+1<=n && c[chd]<c[chd+1]) ++chd;if (c[chd] > x) c[cur] = c[chd];else break;cur = chd, chd <<= 1;}c[cur] = x;
}
void heap_sort(int c[], int n) {for (int i = n>>1; i; --i) adjust(i, n);for (int i = n, j; i > 1;) {std::swap(c[i--], c[1]);adjust(1, i);}
}
int main() {freopen("1.in", "r", stdin);scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", c + i);heap_sort(c, n);for (int i = 1; i <= n; ++i)printf("%d ", c[i]);return 0;
}
快速排序(不稳定)
#include <iostream>
#include <algorithm>
const int N = 1e5 + 7;
int a[N];
void qsort(int lo, int hi) {int i = lo, j = hi, mid = a[lo+hi>>1];//分割操作,lo~j均不大于mid,i~hi均不小于midwhile (i <= j) {while (a[i] < mid) ++i;while (a[j] > mid) --j;if (i <= j) std::swap(a[i++], a[j--]);}if (lo < j) qsort(lo, j);if (i < hi) qsort(i, hi);
}
int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", a + i);qsort(1, n);for (int i = 1; i <= n; ++i) printf("%d ", a[i]);return 0;
}
希尔排序(Shell_sort(int a[], int n))
- Hibbard 增量序列,Dk=2k−1D_k=2^k-1Dk=2k−1,相邻元素互质
- 最坏情况:T=θ(N3/2)T=\\theta(N^{3/2})T=θ(N3/2)
- 猜想:Tavg=O(N5/4)T_{avg}=O(N^{5/4})Tavg=O(N5/4)
- Sedgewick 增量序列
- {1,5,19,41,109,…}\\{1,5,19,41,109,\\dots \\}{1,5,19,41,109,…},由 9×4i−9×2i+19\\times 4^i-9\\times 2^i+19×4i−9×2i+1 或 4i−3×2i+14^i-3\\times 2^i+14i−3×2i+1 按序取出的。
- 猜想:Tavg=O(N7/6),Tworst=O(N4/3)T_{avg}=O(N^{7/6}), T_{worst}=O(N^{4/3})Tavg=O(N7/6),Tworst=O(N4/3)
#include <cstdio>
#include <cmath>
const int N = 107, INF = 2e9;
int s[30], c, a[N];
// void Shell_sort(int a[], int n) {
// //为保持增量元素互质,避免一竖列已排序时,小增量不起作用,白用功
// //采用Hibbard增量序列,Dk = 2^k - 1, O(n^(4/3))
// for (int i = 1<<((int)floor(log(n)/log(2)))-1; i; i = (i+1>>1)-1)
// for (int j = i+1, k, x; j <= n; ++j) {
// for (k = j-i, x = a[j]; k>0 && x<a[k]; k -= i)
// a[k+i] = a[k];
// a[k+i] = x;
// }
// }
int calc() {//计算Sedgewick增量序列,u(i)=9*4^i-9*2^i+1和v(i)=4^i-3*2^i+1//恰好构成差位为2的递增序列,u(i) < v(i+2), O(n^(7/6))for (int i = 0; i <= 13; ++i) {int u = 9*(1<<(i<<1))-9*(1<<i)+1;int t = i + 2, v = (1<<(t<<1))-3*(1<<t)+1;if (u>=1 && u<=INF) s[++c] = u;if (v>=1 && v<=INF) s[++c] = v;}
}
void Shell_sort(int a[], int n) {//为保持增量元素互质,避免一竖列已排序时,小增量不起作用,白用功//采用Sedgewick增量序列while (s[c] >= n) --c;do {int u = s[c];for (int j = u+1, k, x; j <= n; ++j) {for (k = j-u, x = a[j]; k>0 && x<a[k]; k -= u)a[k+u] = a[k];a[k+u] = x;}} while (--c);
}
int main() {freopen("1.in", "r", stdin);int n;scanf("%d", &n);for (int i = 1; i <= n; ++i) scanf("%d", a + i);calc();Shell_sort(a, n);for (int i = 1; i <= n; ++i) printf("%d ", a[i]);return 0;
}
