【数据结构】——6.3 二叉搜索树

一、二叉搜索树的概念

二叉搜索树（Binary Search Tree）：也叫二叉排序树或二叉查找树。

二叉查找树有以下特性：

1. 左子树的所有值比当前节点小，右子树的所有值比当前节点大
2. 左右子树都是二叉搜索树
3. 空树或仅有一个结点的树也是一个二叉搜索树

以下便是一个二叉搜索树：

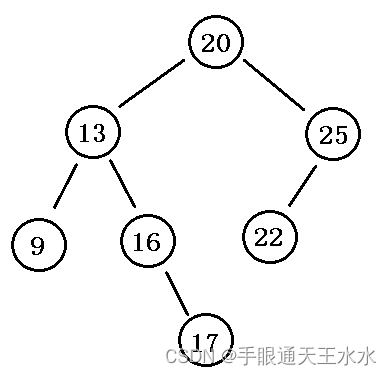
注意：在二叉搜索树中，左子树中所有节点的值都比当前节点小，右子树中所有节点的值都比当前节点大，而不是仅有左孩子比当前节点小，右孩子比当前节点大

如以下所示：17是右子树的节点，但是却比20小，所以该树不是二叉搜索树

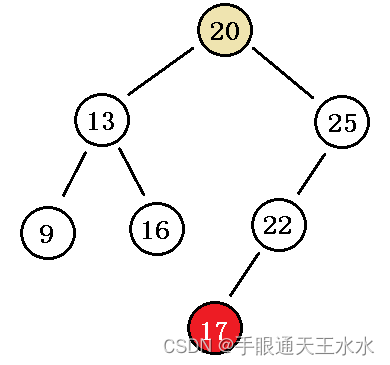
二叉搜索树的每个节点左孩子一定比当前节点小，右孩子一定比当前节点大。

因此它在查找值的时候，不需要遍历整个二叉树，而是只需要判断查找值是否比当前节点小，如果是则走左边走，如果不是，则往右边走，极大得提高了查找的效率，二叉搜索树因此而得名。

在以下二叉树中查找值为17的节点：

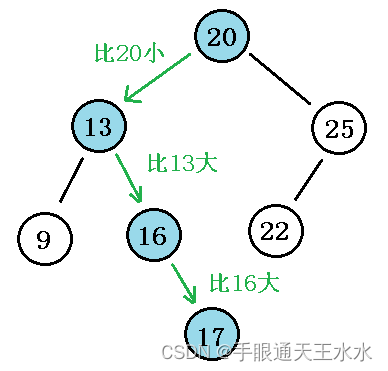
二叉搜索树在查找结点时，最坏的结果只需要遍历树的深度个节点，不需要遍历整个树的所有节点，而在二叉搜索树接近平衡时，查询的时间复杂度仅有O(log2n)O(log_2n)O(log2​n)。

而且二叉树因为这个特性，它的中序遍历结果是有序的。并且不能存储重复的数据，通常也被用来去重和排序。

二、二叉搜索树的实现

1. 存储结构和实现接口

对于二叉搜索树，我们使用二叉树来存储

1. 在二叉搜索树中，存储的数据不允许重复，它们被称为键（Key）。但是库里面有可重复的二叉搜索树供我们使用，只需要将重复数据统一放在当前节点的左边或右边即可，我们不实现可重复的版本
2. 由于我们需要二叉搜索树中可以存储任意类型的数据，因此我们使用模板编程
3. 对于增、删、查操作，我们还会给出递归和非递归的实现版本

二叉搜索树的接口非常少，我们只实现如下所示的接口：

namespace Name
{// 节点类型template<class K>struct BSTNode{BSTNode* _left;			// 左孩子指针BSTNode* _right;		// 右孩子指针K _key;					// 键// 构造函数BSTNode(const K& key): _key(key), _left(nullptr), _right(nullptr){;}};// 二叉搜索树的实现template<class K>class BSTree{typedef BSTNode<K> Node;	// 将节点类型重命名为Nodepublic:bool Insert(const K& key);	// 插入bool Erase(const K& key);	// 删除bool Find(const K& key);	// 查找void InOrder(void);			// 中序遍历bool InsertR(const K& key);	// 插入，递归版本bool EraseR(const K& key);	// 删除，递归版本bool FindR(const K& key);	// 查找，递归版本private:Node* _root;	// 根节点指针};
}

2. 方法的实现

2.1 默认成员函数

（1）构造函数

只需要将头指针置为空即可

// 默认构造函数
BSTree(void): _root(nullptr)
{;
}

（2）析构函数

1. 搜索二叉树的析构过程使用后序遍历，依次释放节点
2. 我们使用递归的方式遍历树，析构函数中不允许有参数，因此我们将后序序遍历的析构过程封装为一个_Destroy函数，再让析构构造去调用它。为了不让外界用户调用_Destroy函数，我们可以将其设为私有

// 析构函数
~BSTree(void)
{_Destroy(_root);_root = nullptr;
}private:
// 后序遍历释放节点
void _Destroy(Node* root)
{if (root == nullptr){return;}_Destroy(root->_left);_Destroy(root->_right);delete root;
}

（3）拷贝构造

1. 拷贝二叉搜索树是将被拷贝的树进行先序遍历，依次拷贝该节点。
2. 我们使用递归的方式遍历树，但是拷贝构造的参数中不能再传入根节点指针。
3. 因此我们将先序遍历的拷贝过程封装为一个_Copy函数，再让拷贝构造去调用它。为了不让外界用户调用_Copy函数，我们可以将其设为私有

// 拷贝构造
BSTree(const BSTree& t)
{_root = _Copy(_root, t._root);
}private:
// 先序遍历递归拷贝节点
Node* _Copy(Node* root, const Node* src)
{if (src == nullptr){return nullptr;}root = new Node(src->_key);root->_left = _Copy(root->_left, src->_left);root->_right = _Copy(root->_right, src->_right);return root;
}

（4）赋值重载

1. 我们依然是使用临时对象拷贝构造被复制对象，然后让自己夺取临时对象的数据
2. 如果直接使用赋值获取临时对象的内容，临时对象析构时会释放自己的空间，导致内存泄漏。因此使用swap交换，让临时对象析构时顺便释放掉自己原来的空间

// 赋值重载函数
BSTree& operator=(const BSTree& t)
{if (this != &t){BSTree temp(t);std::swap(temp._root, _root);}return *this;
}

2.2 查找find

1. 当二叉树非空时，判断当前节点的大小，比该节点小的往左走，比该节点大的往右走，直到找到该节点。
2. 找到该节点返回true，没找到返回false。查找只是看该key值是否存在，二叉搜索树如果允许被随意修改会破坏二叉搜索树的存储结构

（1）非递归实现：

bool Find(const K& key)
{Node* cur = _root;while (cur != nullptr){if (key < cur->_key){// 比当前节点小，往左走cur = cur->_left;}else if (key > cur->_key){// 比当前节点大，往右走cur = cur->_right;}else{// 与当前节点相等，返回truereturn true;}}return false;
}

（2）递归实现：

由于根节点指针_root是类的私有变量，所以用户无法使用对象传入根节点指针，而递归需要根节点指针作为参数，所以我们将递归过程封装成一个_FindR函数，并将其设为私有函数，让FindR函数调用它来完成递归。

// 查找key，递归实现
bool FindR(const K& key)
{return _FindR(_root, key);
}private:
// 查找的递归过程
bool _FindR(Node* root, const K& key)
{if (root == nullptr){return false;}if (key < root->_key){return _FindR(root->_left, key);}else if (key > root->_key){return _FindR(root->_right, key);}else{return true;}
}

2.3 插入insert

1. 当二叉搜索树为空时，直接将节点挂到_root指针上
2. 当二叉树非空时，判断当前节点的大小，比该节点小的往左走，比该节点大的往右走，直到走到根节点，插入指定位置。
3. 如果查找过程出现与插入值一样的节点，则返回false

（1）非递归实现：

bool Insert(const K& key)
{Node* newNode = new Node(key);if (_root == nullptr){_root = newNode;}else{// 查找插入位置Node* parent = nullptr, * cur = _root;while (cur != nullptr){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{return false;}}// 插入节点if (key < parent->_key){parent->_left = newNode;}else if (key > parent->_key){parent->_right = newNode;}}return true;
}

（2）递归实现：

当遍历到根节点时，我们需要在根节点处插入新节点。因此我们要用指针记录被插入的根节点，可以让当前节点的左右孩子为空作为终止条件。

但是我们现在使用的是C++语法，就多了一个选择，将root指针设置为指针的引用类型，那么我们直接对参数root做出修改就可以将新节点连接到二叉搜索树中

// 插入的递归实现
bool InsertR(const K& key)
{return _InsertR(_root, key);
}private:
// 插入的递归过程
bool _InsertR(Node*& root, const K& key)	// root的类型为指针的引用类型
{if (root == nullptr){// 遍历到根节点，创建节点并插入root = new Node(key);		// 可以直接改变二叉搜索树的内容return true;}// 查找插入位置if (key < root->_key){return _InsertR(root->_left, key);}else if (key > root->_key){return _InsertR(root->_right, key);}else{return false;}
}

2.4 删除erase

（1）实现思路

1. 当被删除的节点是叶子节点时，直接删除就可以了
2. 当被删除的节点只有一个孩子时，直接删除它，并让它的父节点领养它的孩子
3. 当被删除的节点有2个孩子时，直接删除是比较麻烦的，我们可以在它的左右子树里找一个叶子节点替换它，然后删除这个叶子节点即可

那么哪些叶子节点能与被删除节点进行交换呢？

1. 左子树最大值，在左子树的最右边位置：

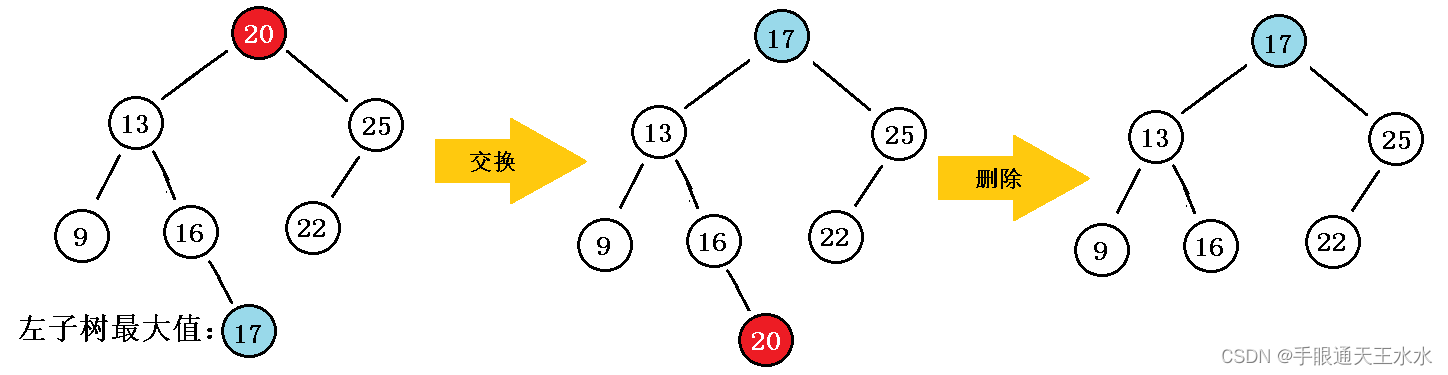
2. 右子树最小值，在右子树的最左边位置：

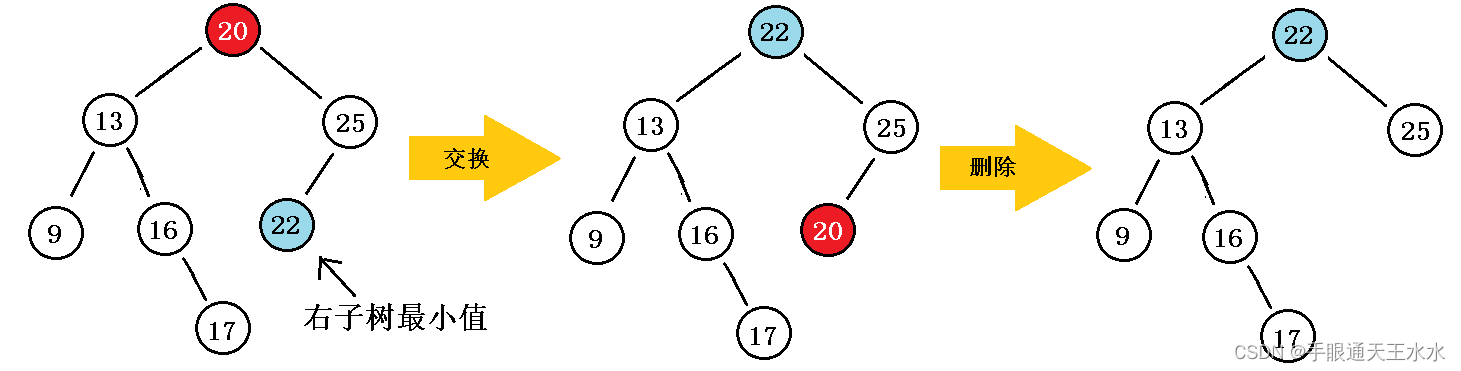
（2）非递归实现

bool Erase(const K& key)
{// 查找被删除节点Node* cur = _root, *parent = _root;while (cur != nullptr){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{// 删除keyif (cur->_left == nullptr){// 没有左子树，继承右子树if (_root == cur){// 被删除节点为根节点_root = cur->_right;}else{// 被删除节点为非根节点if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){// 只有左子树，继承左子树if (_root == cur){// 被删除节点为根节点_root = cur->_left;}else{// 被删除节点为非根节点if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}	else{// 左右子树都有，选右边最小Node* minParent = cur, * min = cur->_right;while (min->_left != nullptr){minParent = min;min = min->_left;}cur->_key = min->_key;if (min == minParent->_right)minParent->_right = min->_right;elseminParent->_left = min->_right;delete min;}return true;}}return false;
}

（3）递归实现：

1. 这里的递归过程依然要提取成一个函数，并且参数用引用类型
2. 递归删除被交换的叶子节点时，要从被删节点的位置重新向下找，因为使用局部变量找到的叶子节点指针是局部变量，参数中的引用类型会改变局部变量的值，而不会改变二叉搜索树中的内容。

bool _EraseR(Node*& root, const K& key)
{if (root == nullptr){return false;}// 查找被删节点if (key < root->_key){return _EraseR(root->_left, key);}else if (key > root->_key){return _EraseR(root->_right, key);}else{Node* del = nullptr;if (root->_left == nullptr){// 只有左孩子del = root;root = root->_right;}else if (root->_right == nullptr){// 只有右孩子del = root;root = root->_left;}else{// 有两个孩子（交换左子树最大值）Node* max = root->_left;while (max->_right != nullptr){max = max->_right;}std::swap(max->_key, root->_key);// return _EraseR(max, key);	max是函数的局部变量，参数中的引用类型更改的不是原树中的指针return _EraseR(root->_left, key);	// 继续向下遍历删除被交换过的叶子节点}delete del;return true;}
}

2.5 中序遍历

中序遍历的递归过程也是要独立封装成函数

// 中序遍历
void InOrder(void)
{_InOrder(_root);std::cout << std::endl;
}// 中序遍历的递归过程
void _InOrder(Node* root)
{if (root == nullptr){return;}_InOrder(root->_left);std::cout << root->_key << " ";_InOrder(root->_right);
}