D. Returning Home(建图 + 堆优化最短路)

Problem - D - Codeforces

Yura已经走了一段时间了，正打算回家。他得尽快回家。为了做到这一点，Yura可以使用城市周围的即时移动位置。我们把城市表示成n × n个街区的面积。Yura需要从坐标(S, Sy)的块移动到坐标(fa, fy)的块。在一分钟内，Yura可以移动到任何相邻的侧块;换句话说，他可以向四个方向移动。此外，在城市中有m个即时移动地点。你和尤拉都知道他们的坐标。如果Yura位于与该位置具有相同坐标z或相同坐标y的块中，他可以立即移动到即时移动位置。帮助Yura找到回家所需的最短时间。

输入第一行包含两个整数n和m——城市的大小和瞬时移动位置的数量(1 < n <10°，0<m<105)。下一行包含四个整数S她嘘——Yura最初所处位置的坐标及他家的坐标(1<S， Syfafy<n）.接下来的m行每一行包含两个整数xi yi -第i个瞬时移动位置的坐标(1 < xi, yi ns)。输出在唯一一行打印出回家所需的最短时间。

Examples

input

Copy

5 3
1 1 5 5
1 2
4 1
3 3

output

Copy

5

input

Copy

84 5
67 59 41 2
39 56
7 2
15 3
74 18
22 7

output

Copy

42

请注意在第一个例子中，Yura需要从(1,1)到达(5,5)。他可以在5分钟内先使用第二个即时移动位置(因为它的y坐标等于Yura的y坐标)，然后步行(4,1)→(4,2)→(4,3)→(5,3)→(5,4)→(5,5)。

题解:
果然图论建图才是最难的,

对于每个瞬移点,起点到其距离应该是min(abs(sx - x),abs(sy - y)),

瞬移点到终点的距离是abs(ex - x) + abs(ey - y)

这点很容易写出来

关键是瞬移点与瞬移点的距离不好建图

暴力m*m肯定会t

通过观察我们发现,先对x坐标从大到小排序

如果是这种, A - C的最短距离肯定是A - B的最短 +  B - C的最短

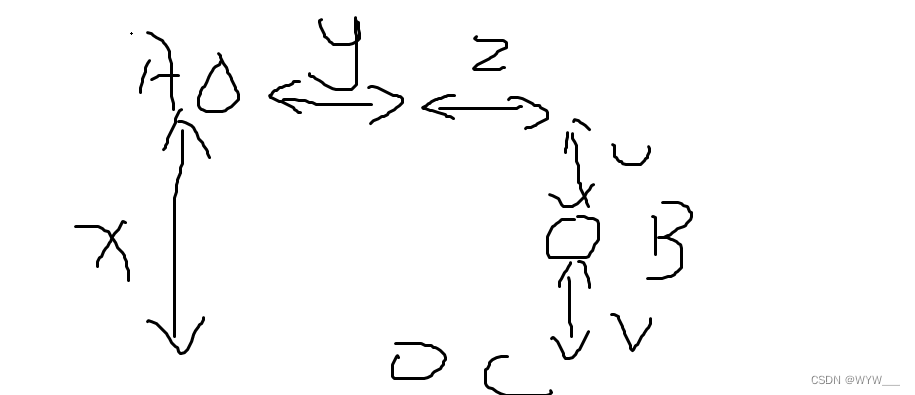
但是如果是这种情况就不成立了

所以也要对y进行一次排序,相邻建图

还有一点就是跑堆优化最短路时,这里有符号整数溢出

 wa40

改成这样就AC了

 不太清楚为什么,以后尽量用第二种吧

#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
#define int long long
vector<PII> p[200050];
int n,m;
int sx,sy,ex,ey;
struct node
{int x,y,id;
}a[200050];
int dis[200050];
int cmpx(node a,node b)
{return a.x < b.x;
}
int cmpy(node a,node b)
{return a.y < b.y;
}
void solve()
{cin >> n >> m;cin >> a[m + 1].x >> a[m + 1].y >> a[m + 2].x >> a[m + 2].y;dis[m + 1] = dis[m + 2] = 2e18;for(int i = 1;i <= m;i++){dis[i] = 2e18;cin >> a[i].x >> a[i].y;a[i].id = i;p[m + 1].push_back({min(abs(a[m + 1].x - a[i].x),abs(a[m + 1].y - a[i].y)),i});p[i].push_back({min(abs(a[m + 1].x - a[i].x),abs(a[m + 1].y - a[i].y)),m + 1}); p[i].push_back({abs(a[m + 2].x - a[i].x) + abs(a[m + 2].y - a[i].y),m + 2});p[m + 2].push_back({abs(a[m + 2].x - a[i].x) + abs(a[m + 2].y - a[i].y),i});}sort(a + 1,a + 1 +m,cmpx);for(int i = 2;i <= m;i++){int u = a[i - 1].id;int v = a[i].id;int w = min(abs(a[i - 1].x - a[i].x),abs(a[i - 1].y - a[i].y));p[u].push_back({w,v});p[v].push_back({w,u});}sort(a + 1,a + 1 +m,cmpy);for(int i = 2;i <= m;i++){int u = a[i - 1].id;int v = a[i].id;int w = min(abs(a[i - 1].x - a[i].x),abs(a[i - 1].y - a[i].y));p[u].push_back({w,v});p[v].push_back({w,u});}	priority_queue<PII,vector<PII>,greater<PII>>q;dis[m + 1] = 0;q.push({0, m + 1});while(q.size()){PII t = q.top();q.pop();for(PII ne:p[t.second]){if(dis[ne.second] > dis[t.second] + ne.first){dis[ne.second] = dis[t.second] + ne.first;q.push({dis[ne.second],ne.second});}}}cout << min(dis[m + 2],abs(a[m + 1].x - a[m + 2].x) + abs(a[m + 2].y - a[m + 1].y));
}signed main()
{
//	ios::sync_with_stdio(0);
//	cin.tie(0);cout.tie(0);int t = 1;
//	cin >> t;while(t--){solve(); }
}