算法套路九——二叉树广度优先遍历（层序遍历）

算法示例LeetCode102. 二叉树的层序遍历

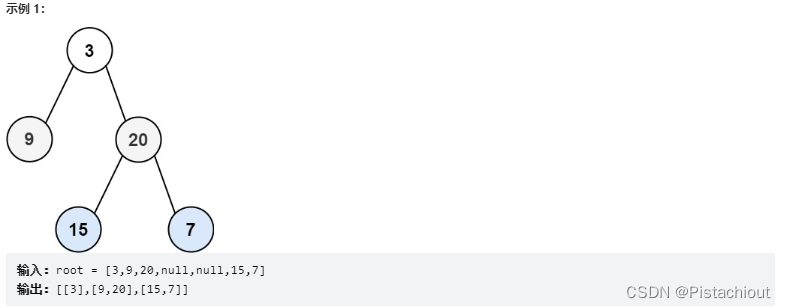
给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

法一：双数组

在层序遍历时采用两个数组来记录，如下图所示，cur记录当前结点，通过遍历cur将cur中的节点的子结点放入nxt中，同时将cur值记录在vlas中，之后令cur=nxt重新遍历cur。


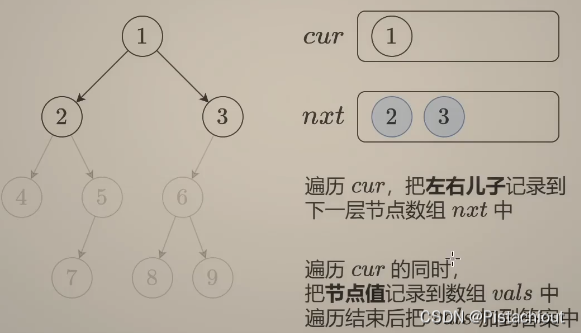
cur为空时即所有结点遍历完成，退出循环。

class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if root is None:return []cur=[root]ans=[]while cur:nxt=[]vals=[]for node in cur:vals.append(node.val)if node.left: nxt.append(node.left)if node.right:nxt.append(node.right)cur=nxtans.append(vals)return ans

法二：队列

与两个数组类似，队列中首先存当前遍历的节点，之后根据当前队列的长度遍历队列，将每个节点的左右子结点加入队列中，并将队列最左侧元素出队。

class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if root is None:return []q=deque([root])ans=[]while q:vals=[]for _ in range(len(q)):node=q.popleft()vals.append(node.val)if node.left: q.append(node.left)if node.right:q.append(node.right)ans.append(vals)return ans

这两种方法只有细微的地方有代码的区别，故可以选一种自己认为比较顺手的作为常用解法

算法练习一：LeetCode103. 二叉树的锯齿形层序遍历

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

本题与上题类似，只是需要增加一个bool变量even记录当前层数是否为偶数，若为偶数，则需要在将值添加进vals进行反向添加，即vals[len(cur)-1-i]=node.Val

法一：双数组

func zigzagLevelOrder(root *TreeNode) (ans [][]int) {if root==nil{return }cur:=[]*TreeNode{root}even:=falsefor len(cur)>0{nxt:=[]*TreeNode{}vals:=make([]int,len(cur))for i,node:=range cur{if even{vals[len(cur)-1-i]=node.Val}else{vals[i]=node.Val }if node.Left != nil {nxt  = append(nxt , node.Left)}if node.Right != nil { nxt  = append(nxt , node.Right)}}cur=nxteven = !evenans=append(ans,vals)}return
}

法二：队列

func zigzagLevelOrder(root *TreeNode) (ans [][]int) {if root==nil{return }q:=[]*TreeNode{root}even:=falsefor len(q)>0{n:=len(q)vals:=make([]int,n)for i:=0;i<n;i++{//对遍历变量有修改时，不能使用for range遍历node:=q[0]q=q[1:]if even{vals[n-1-i]=node.Val}else{vals[i]=node.Val }if node.Left != nil {q = append(q, node.Left)}if node.Right != nil { q = append(q, node.Right)}}ans=append(ans,vals)even=!even}return
}

算法练习二：LeetCode104. 二叉树的最大深度

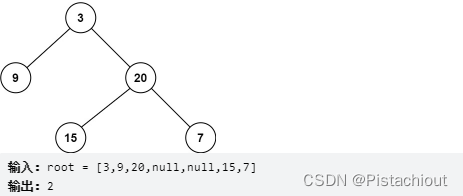
给定一个二叉树，找出其最大深度。

本题在之前使用了递归解决，这里使用广度优先层序遍历队列来解决

法一：双数组

func maxDepth(root *TreeNode)  int {if root==nil{return 0}cur:=[]*TreeNode{root}maxD:=0for len(cur)!=0{nxt:=[]*TreeNode{}maxD++for _,node:=range cur{if node.Left!=nil{nxt=append(nxt,node.Left)}if node.Right!=nil{nxt=append(nxt,node.Right)}}cur=nxt }return maxD
}

法二：队列

func maxDepth(root *TreeNode)  int {if root==nil{return 0}q:=[]*TreeNode{root}maxD:=0for len(q)!=0{maxD++n:=len(q)for i:=0;i<n;i++{node:=q[0]q=q[1:]if node.Left!=nil{q=append(q,node.Left)}if node.Right!=nil{q=append(q,node.Right)}}}return maxD
}

算法练习三：LeetCode111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

使用广度优先搜索的方法遍历整棵树。
当我们找到一个叶子节点时，直接返回这个叶子节点的深度。层序遍历的性质保证了最先搜索到的叶子节点的深度一定最小。

func minDepth(root *TreeNode) int {if root==nil{return 0}minD:=0q:=[]*TreeNode{root}for len(q)!=0{minD++n:=len(q)for i:=0;i<n;i++{node:=q[0]q=q[1:]if node.Left==nil&&node.Right==nil{return minD}if node.Left!=nil{q=append(q,node.Left)}if node.Right!=nil{q=append(q,node.Right)}}}return -1
}

算法进阶一：LeetCode513. 找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。假设二叉树中至少有一个节点。

此题有一定难度，因为是要找到最底层最左边节点的值，想到层序遍历，那么如何得到最左边的节点呢，我们可以在进行层序遍历时每次都从右往左入队，这样每次都是上层、右边的节点先出队，故最底层最左边的节点最后出队

func findBottomLeftValue(root *TreeNode) int {q:=[]*TreeNode{root}var node *TreeNodefor len(q)>0{node=q[0]q=q[1:]if node.Right!=nil{q=append(q,node.Right)}if node.Left!=nil{q=append(q,node.Left)}}return node.Val
}

算法进阶二：LeetCode199. 二叉树的右视图

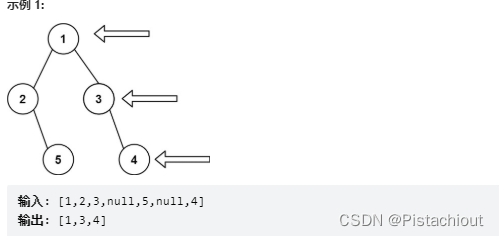
给定一个二叉树的 根节点 root，想象站在它的右侧，按照从顶部到底部的顺序，返回从右侧能看到的节点值。

此题之前使用深度遍历递归时有一定难度，但如果使用广度优先的层序遍历，则很明显，只需要记录队列每一层的最后一个结点即可

func rightSideView(root *TreeNode) []int {if root==nil{return []int{}}ans:=[]int{}q:=[]*TreeNode{root}for len(q)!=0{n:=len(q)for i:=0;i<n;i++{node:=q[0]q=q[1:]if node.Left!=nil{q=append(q,node.Left)}if node.Right!=nil{q=append(q,node.Right)}if i==n-1{ans=append(ans,node.Val)}}   }return ans
}