小白学Pytorch系列--Torch.optim API Algorithms(2)

小白学Pytorch系列–Torch.optim API Algorithms(2)
| 方法 | 注释 |
|---|---|
| Adadelta | 实现Adadelta算法。 |
| Adagrad | 实现Adagrad算法。 |
| Adam | 实现Adam算法。 |
| AdamW | 实现AdamW算法。 |
| SparseAdam | 实现了适用于稀疏张量的懒惰版Adam算法。 |
| Adamax | 实现Adamax算法(一种基于无限范数的Adam算法)。 |
| ASGD | 实现平均随机梯度下降。 |
| LBFGS | 实现L-BFGS算法,很大程度上受到minFunc的启发。 |
| NAdam | 实现NAdam算法。 |
| RAdam | 实现了RAdam算法。 |
| RMSprop | 实现RMSprop算法。 |
| Rprop | 实现了弹性反向传播算法。 |
| SGD |
Adadelta
Adadelta是一种自适应学习率的优化算法,它与RMSprop相似,但引入了一个衰减系数来平衡历史梯度平方和目标函数变化量。在PyTorch中,可以通过设置optim.Adadelta()来使用该优化器。

grad = grad.add(param, alpha=weight_decay)
square_avg.mul_(rho).addcmul_(grad, grad, value=1 - rho)
std = square_avg.add(eps).sqrt_()
delta = acc_delta.add(eps).sqrt_().div_(std).mul_(grad)
acc_delta.mul_(rho).addcmul_(delta, delta, value=1 - rho)
param.add_(delta, alpha=-lr)

Adagrad
AdaGrad是一种自适应学习率的优化算法,在更新参数时根据历史梯度信息来动态调整每个参数的学习率。

源码
grad = grad.add(param, alpha=weight_decay)
clr = lr / (1 + (step - 1) * lr_decay)
state_sum.addcmul_(grad, grad, value=1)
std = state_sum.sqrt().add_(eps)
param.addcdiv_(grad, std, value=-clr)

Adam
Adam是一种融合了动量梯度下降和自适应学习率的优化算法,在更新参数时既考虑历史梯度的加权平均又考虑历史梯度平方的加权平均。

源码
grad = grad.add(param, alpha=weight_decay)
exp_avg.mul_(beta1).add_(grad, alpha=1 - beta1)
exp_avg_sq.mul_(beta2).addcmul_(grad, grad.conj(), value=1 - beta2)
if amsgrad:# Maintains the maximum of all 2nd moment running avg. till nowtorch.maximum(max_exp_avg_sqs[i], exp_avg_sq, out=max_exp_avg_sqs[i])# Use the max. for normalizing running avg. of gradientdenom = (max_exp_avg_sqs[i].sqrt() / math.sqrt(bias_correction2)).add_(eps)
else:denom = (exp_avg_sq.sqrt() / math.sqrt(bias_correction2)).add_(eps)step_size = lr / bias_correction1
param.addcdiv_(exp_avg, denom, value=-step_size)
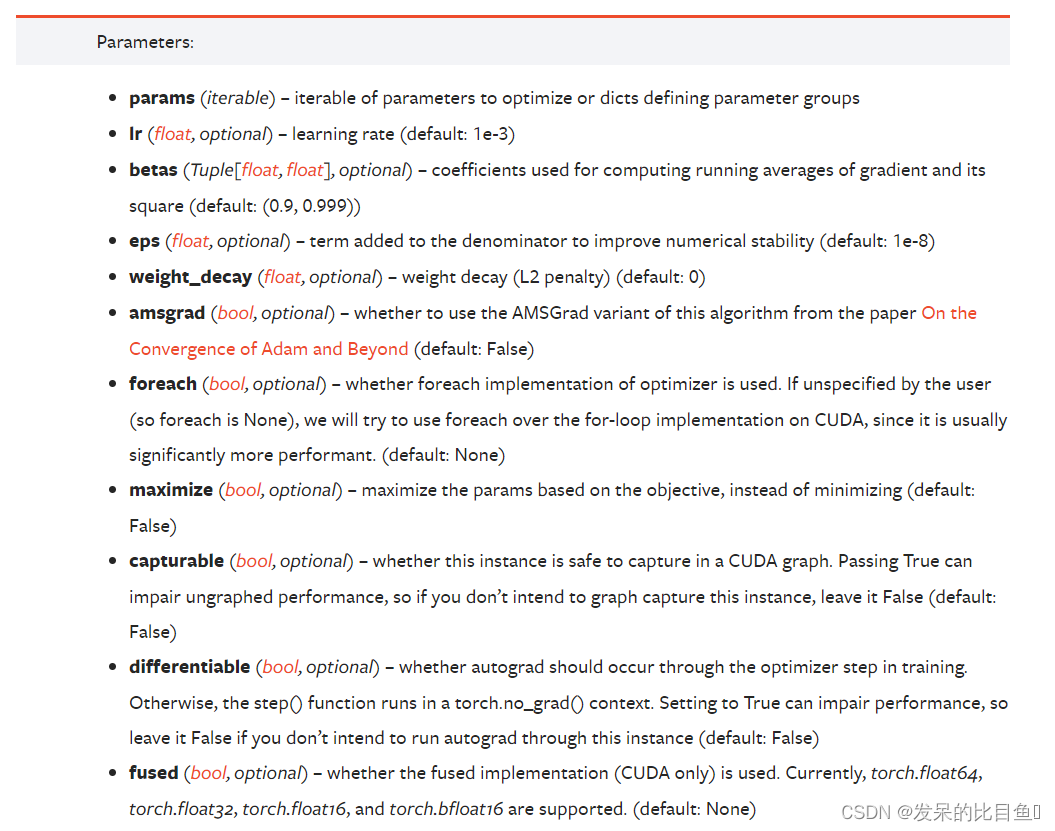
AdamW
AdamW是一种基于Adam优化算法的变体,它引入了权重衰减(weight decay)来解决Adam可能存在的参数过度拟合问题。

源码
# Perform stepweight decay
param.mul_(1 - lr * weight_decay)bias_correction1 = 1 - beta1 step
bias_correction2 = 1 - beta2 step# Decay the first and second moment running average coefficient
exp_avg.mul_(beta1).add_(grad, alpha=1 - beta1)
exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value=1 - beta2)
if amsgrad:# Maintains the maximum of all 2nd moment running avg. till nowtorch.maximum(max_exp_avg_sqs[i], exp_avg_sq, out=max_exp_avg_sqs[i])# Use the max. for normalizing running avg. of gradientdenom = (max_exp_avg_sqs[i].sqrt() / math.sqrt(bias_correction2)).add_(eps)
else:denom = (exp_avg_sq.sqrt() / math.sqrt(bias_correction2)).add_(eps)step_size = lr / bias_correction1param.addcdiv_(exp_avg, denom, value=-step_size)
SparseAdam

Adamax


ASGD

LBFGS

NAdam


RAdam


RMSprop
RMSprop是一种自适应学习率的优化算法,在更新参数时根据历史梯度平方的加权平均来动态调整每个参数的学习率。

源码
grad = grad.add(param, alpha=weight_decay)square_avg.mul_(alpha).addcmul_(grad, grad, value=1 - alpha)
if centered:grad_avg = grad_avgs[i]grad_avg.mul_(alpha).add_(grad, alpha=1 - alpha)avg = square_avg.addcmul(grad_avg, grad_avg, value=-1).sqrt_().add_(eps)
else:avg = square_avg.sqrt().add_(eps)if momentum > 0:buf = momentum_buffer_list[i]buf.mul_(momentum).addcdiv_(grad, avg)param.add_(buf, alpha=-lr)
else:param.addcdiv_(grad, avg, value=-lr)

Rprop


SGD
梯度下降包括: 批量梯度下降(Batch Gradient Descent)、随机梯度下降(Stochastic Gradient Descent)、小批量梯度下降(Mini-batch Gradient Descent)、动量梯度下降(Momentum Gradient Descent)
可选动量梯度下降是一种在梯度下降更新过程中加入动量项的优化算法,可以加速收敛并减少震荡。在PyTorch中,可以通过设置momentum参数实现动量梯度下降。

源码
d_p = d_p_list[i]
if weight_decay != 0:d_p = d_p.add(param, alpha=weight_decay)if momentum != 0:buf = momentum_buffer_list[i]if buf is None:buf = torch.clone(d_p).detach()momentum_buffer_list[i] = bufelse:buf.mul_(momentum).add_(d_p, alpha=1 - dampening)if nesterov:d_p = d_p.add(buf, alpha=momentum)else:d_p = bufalpha = lr if maximize else -lr
param.add_(d_p, alpha=alpha)

批量梯度下降
import torch
import matplotlib.pyplot as plt# 定义训练数据
X = torch.tensor([1, 2, 3, 4], dtype=torch.float32)
Y = torch.tensor([2, 4, 6, 8], dtype=torch.float32)# 初始化模型参数
w = torch.tensor(0.0, requires_grad=True)
b = torch.tensor(0.0, requires_grad=True)# 定义损失函数
loss_fn = torch.nn.MSELoss()# 定义优化器和超参数
optimizer = torch.optim.SGD([w, b], lr=0.01)
epochs = 100# 批量梯度下降
for epoch in range(epochs):# 前向传播Y_pred = w * X + b# 计算损失loss = loss_fn(Y_pred, Y)# 反向传播loss.backward()# 更新参数optimizer.step()# 清空梯度optimizer.zero_grad()# 输出结果
print(f"w = {w.item()}, b = {b.item()}")# 绘制拟合直线
plt.scatter(X.numpy(), Y.numpy())
plt.plot(X.numpy(), (w * X + b).detach().numpy(), 'r')
plt.show()随机梯度下降
import torch
import matplotlib.pyplot as plt# 定义训练数据
X = torch.tensor([1, 2, 3, 4], dtype=torch.float32)
Y = torch.tensor([2, 4, 6, 8], dtype=torch.float32)# 初始化模型参数
w = torch.tensor(0.0, requires_grad=True)
b = torch.tensor(0.0, requires_grad=True)# 定义损失函数和优化器
loss_fn = torch.nn.MSELoss()
optimizer = torch.optim.SGD([w, b], lr=0.01)# 定义超参数
batch_size = 1
epochs = 100# 随机梯度下降
for epoch in range(epochs):# 创建DataLoaderloader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(X, Y), batch_size=batch_size, shuffle=True)for x_batch, y_batch in loader:# 前向传播y_pred = w * x_batch + b# 计算损失loss = loss_fn(y_pred, y_batch)# 反向传播loss.backward()# 更新参数optimizer.step()# 清空梯度optimizer.zero_grad()# 输出结果print(f"w = {w.item()}, b = {b.item()}")# 绘制拟合直线
plt.scatter(X.numpy(), Y.numpy())
plt.plot(X.numpy(), (w * X + b).detach().numpy(), 'r')
plt.show()小批量梯度下降
import torch
import matplotlib.pyplot as plt# 定义训练数据
X = torch.tensor([1, 2, 3, 4], dtype=torch.float32)
Y = torch.tensor([2, 4, 6, 8], dtype=torch.float32)# 初始化模型参数
w = torch.tensor(0.0, requires_grad=True)
b = torch.tensor(0.0, requires_grad=True)# 定义损失函数和优化器
loss_fn = torch.nn.MSELoss()
optimizer = torch.optim.SGD([w, b], lr=0.01)# 定义超参数
batch_size = 2
epochs = 100# 小批量梯度下降
for epoch in range(epochs):# 创建DataLoaderloader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(X, Y), batch_size=batch_size, shuffle=True)for x_batch, y_batch in loader:# 前向传播y_pred = w * x_batch + b# 计算损失loss = loss_fn(y_pred, y_batch)# 反向传播loss.backward()# 更新参数optimizer.step()# 清空梯度optimizer.zero_grad()# 输出结果
print(f"w = {w.item()}, b = {b.item()}")# 绘制拟合直线
plt.scatter(X.numpy(), Y.numpy())
plt.plot(X.numpy(), (w * X + b).detach().numpy(), 'r')
plt.show()动量梯度下降
import torch
import matplotlib.pyplot as plt# 定义训练数据
X = torch.tensor([1, 2, 3, 4], dtype=torch.float32)
Y = torch.tensor([2, 4, 6, 8], dtype=torch.float32)# 初始化模型参数和动量
w = torch.tensor(0.0, requires_grad=True)
b = torch.tensor(0.0, requires_grad=True)
momentum = 0.9# 定义损失函数和优化器
loss_fn = torch.nn.MSELoss()
optimizer = torch.optim.SGD([w, b], lr=0.01, momentum=momentum)# 定义超参数
epochs = 100# 动量梯度下降
for epoch in range(epochs):# 前向传播y_pred = w * X + b# 计算损失loss = loss_fn(y_pred, Y)# 反向传播loss.backward()# 更新参数optimizer.step()# 清空梯度optimizer.zero_grad()# 输出结果
print(f"w = {w.item()}, b = {b.item()}")# 绘制拟合直线
plt.scatter(X.numpy(), Y.numpy())
plt.plot(X.numpy(), (w * X + b).detach().numpy(), 'r')
plt.show()