【机器学习学习笔记】机器学习入门监督学习

文章列表

1. 机器学习入门

1.1 What is Machine Learning?

"Field of study that gives computers the ability to learn without being explicitly programmed. "

——Arthur Samuel (1959)

亚瑟·萨缪尔：跳棋程序编写者

常用机器学习算法：

Supervised learning (more important)
Unsupervised learning

1.2 Supervised learning

监督学习两大类型：

Regression（回归）

Predict a number

infinitely many possible outputs
Classification（分类）

predict categories

small number of possible outputs

1.3 Unsupervised learning

数据只有输入值x，而没有输出的标签值y，算法会在数据中找到结构，进行分类。

Clustering algorithm（聚类）

Group similar data points together
Anomaly detection（异常检测）

Find unusual data points
Dimensionality reduction（降维）

Compress data using fewer numbers

2. Supervised learning

2.1 单元线性回归模型

2.1.1 Linear Regression Model（线性回归模型）

线性回归模型属于监督学习模型，因为数据集中的每个数据都有确定的值，模型将根据值来进行学习。

Terminology（术语）:

Training Set: Data used to train the model

Notation:

$x$ = “input” variable / “input” feature / feature
$y$ = “output” variable / “target” feature /
$m$ = number of training examples
$(x, y)$ = single training example
$x^{(i)}, y^{(i)})$ = $i^{th}$ training example

$\\quad f_{w,b}(x) = wx+b$
“w” means weight / slope, “b” means bias / intercept

2.1.2 Cost Function（代价函数）

显然，我们希望选取的模型能够很好的拟合训练集中的数据，这就需要一个参数来量化当前的拟合程度，这就是Cost Function。其中m表示测试集样本的总数，在公式中用于避免代价函数盲目增大，设置为2m是为了便于求导。
$J(w,b)=12m∑i=1m(y^(i)−y(i))2=12m∑i=1m(fw,b(x(i))−y(i))2J(w,b) = \\frac{1}{2m} \\sum_{i=1}^m (\\hat{y}^{(i)} - y^{(i)})^2 = \\frac{1}{2m} \\sum_{i=1}^m (f_{w,b}(x^{(i)}) - y^{(i)})^2$

可见，代价函数越大，拟合效果越差。于是，线性回归模型的目标就是找到最小的w值，使得 $J (w)$ 最小化；更普遍的情况是，找到最小的w和b值，使得 $J (w, b)$ 最小化。

在经典房价预测案例中，我们选取房屋面积作为特征，根据不同的参数可以得到下面的三维图像，纵坐标为代价函数大小，很直观的看到右图中的代价函数要更小，同时也不难看出右图的取值更好的拟合了测试集。

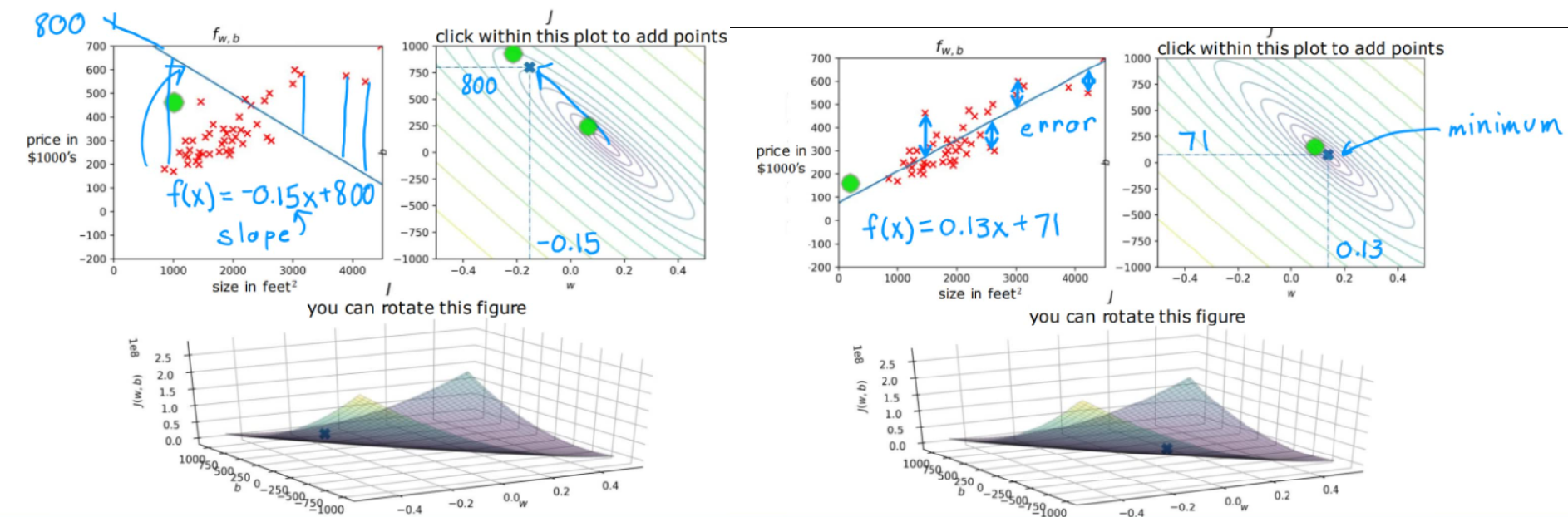
【机器学习学习笔记】机器学习入门监督学习

2.1.3 Gradient Descent（梯度下降）

有了代价函数，如何得到合适的参数值就成为了必须解决的问题。通过Gradient Descent，我们可以获得代价最小的参数w和b。

梯度下降算法广泛应用于机器学习，如线性回归模型和深度学习模型中。

在上面的曲面中，通过不断选择当前坐标坡度最大的方向，最终会到达谷底，谷底即local minima，即局部最小值。

梯度下降算法概述：

让 $w, b$ 以某值开始，通过不断改变 $w, b$ 来降低 $J (w, b)$ ，直到取得或接近 $J (w, b)$ 最小值，即：Repeat until convergence（重复，直到收敛）。
$repeat{w=w−α∂∂wJ(w,b)b=b−α∂∂bJ(w,b)}simultaneousupdates\\begin{align} & repeat\\{ \\\\ &\\qquad w = w - α \\frac{∂}{∂w}J(w,b) \\\\ &\\qquad b = b - α \\frac{∂}{∂b}J(w,b) \\\\ & \\}simultaneous \\quad updates \\end{align}$

$\\ Rate$ ，即学习率，控制梯度下降的步长；

$∂∂w=Derivative\\frac{∂}{∂w} = Derivative$ ，即导数项（偏导数，Partial derivative），控制梯度下降的方向。

2.2 多元线性回归模型

2.2.1 Multiple features (variables)

很多实际情况并不止有一个特征，比如决定房价的不只有面积。对于有多个特征的线性回归模型，我们称为多元线性回归模型。

$x_j$ = $j^{th}$ feature

$n$ = number of features

$x⃗(i)\\vec{x}^{(i)}$ = features of $i^{th}$ training example

$x⃗j(i)\\vec{x}^{(i)}_j$ = value of feature $j$ in $i^{th}$ training example

$\\quad f_{w,b}(x) = w_1x_1+w_2x_2+w_3x_3+w_4x_4+b$
进一步可以表达为：
$fw⃗,b(x⃗)=w⃗⋅x⃗+bf_{\\vec{w},b}(\\vec{x}) = \\vec{w}·\\vec{x}+b$

在Python中，向量的计算可以通过调用NumPy库，实现快速且间接的运算，其中，w和x均为向量

w = np.array([1.0, 2.5, -3.3])
b = 4
x = np.array([10, 20, 30])f = np.dot(w, x) + b

通过向量化运算，计算机同时获取向量的所有数据，并且对两向量的每个维度进行同时运算，然后调用专门的并行处理硬件求和；而左侧的for循环则是依次相乘并累加。显然，使用向量可以节省很大的时间。

2.2.2 针对多元回归的梯度下降

	Previous notation	Vector notation
Parameters	$w_1,···,w_n$ $b$	$w⃗=[w1⋅⋅⋅wn]\\vec{w}=[w_1 ··· w_n]$ $b$
Model	$f_{w,b}(x) = w_1x_1+w_2x_2+w_3x_3+w_4x_4+b$	$fw⃗,b(x⃗)=w⃗⋅x⃗+bf_{\\vec{w},b}(\\vec{x})=\\vec{w}·\\vec{x}+b$
Cost function	$J(w_1,···,w_n,b)$	$J(w⃗,b)J(\\vec{w},b)$
Gradient descent	repeat{ $wj=wj−α∂∂wjJ(w1,⋅⋅⋅,wn,b)w_j=w_j-α\\frac{∂}{∂w_j}J(w_1,···,w_n,b)$ $b=b−α∂∂bJ(w1,⋅⋅⋅,wn,b)b=b-α\\frac{∂}{∂b}J(w_1,···,w_n,b)$ }	repeat{ $wj=wj−α∂∂wjJ(w⃗,b)w_j=w_j-α\\frac{∂}{∂w_j}J(\\vec{w},b)$ $b=b−α∂∂bJ(w⃗,b)b=b-α\\frac{∂}{∂b}J(\\vec{w},b)$ }

【梯度下降法扩展】Normal equation（正规方程法）：

正规方程法：不需要通过迭代即可求得w,b的值，同时只能用在线性回归模型中。

缺点：不适用于其他学习算法，当特征的数量极大时（如大于10000）计算速度减慢。

在实现线性回归的机器学习库中可以使用正规方程方法，但是梯度下降是寻找参数w,b的推荐方法。

2.3 Practical Tips for Linear Regression

2.3.1 Feature Scaling（特征缩放）

下式为房价案例的线性回归模型， $x_1$ 表示房子大小（size，单位：feet²）， $x_2$ 表示卧室数量（#badrooms）
$price^=w1x1+w2x2+b\\hat{price}=w_1x_1+w_2x_2+b$

我们可以假设： $x_1$ 范围为500-2000， $x_2$ 范围为0-5，这都是现实中合理的数据范围，但是当我们给参数 $w_1,w_2$ 不同的值，也会得到不同的效果，左侧数据显然不符合实际，这是因为在经典房价案例中，房屋面积的参数对结果的影响更大，而卧室数量的参数影响则较小。

观察下图中左上坐标系，点的位置由于两特征的范围原因，不利于观察；右上坐标系的等高线也不利于进行梯度下降。如果对变量进行Feature Scaling，即特征缩放，改变他们的相对范围，就会使数据分布更合理，梯度下降速度更快

那么如何进行特征缩放呢？

方法一：

对于房屋案例， $x_1$ 的取值范围是500~2000，只需要进行 $x1,scaled=x12000x_{1,scaled}=\\frac{x_1}{2000}$ ，就可以将之范围缩放到0.15~1

同理， $x_2$ 的取值范围是0~5，只需要进行 $x2,scaled=x25x_{2,scaled}=\\frac{x_2}{5}$ ，就可以将之范围缩放到0~1

方法二：Mean normalization（均值归一化）

通过缩放将数据点聚集在坐标轴原点的四周（意味着有正负值），范围在-1~1之间

首先求 $x_1$ 和 $x_2$ 在训练集上的均值 $μ1\\mu_1$ 和 $μ2\\mu_2$

然后进行： $x1,scaled=x1−μ12000−300x_{1,scaled}=\\frac{x_1-\\mu_1}{2000-300}$ 以及 $x2,scaled=x2−μ25−0x_{2,scaled}=\\frac{x_2-\\mu_2}{5-0}$

这样 $x_1$ 被缩放到-0.18~0.82， $x_2$ 则被缩放到-0.45~0.54

方法三：Z-score normalization（Z-score归一化）

需要为每一个特征进行计算标准差（standard deviation）以及均值

然后进行： $x1,scaled=x1−μ1σ1x_{1,scaled}=\\frac{x_1-\\mu_1}{\\sigma_1}$ 以及 $x2,scaled=x2−μ2σ2x_{2,scaled}=\\frac{x_2-\\mu_2}{\\sigma_2}$

这样 $x_1$ 被缩放到-0.67~3.1， $x_2$ 则被缩放到-1.6~1.9

总而言之，缩放的范围以及缩放应当选择哪个方法都没有具体的规定，但通过缩放，特征的量级应当相同，否则缩放就没有意义了，梯度下降速度也得不到提升。

2.3.2 检查梯度下降是否收敛

我们应当保证梯度下降算法正确工作。为此，可以构建一个横轴为迭代次数（# iterations），纵轴为代价 $J(w⃗,b)J(\\vec{w},b)$ 的坐标轴，正确的图像应当是随着迭代次数增加，代价不断下降直至平缓。我们称这条曲线为学习曲线（learning curve）。

在不同的运用场景中，梯度下降的收敛速度可能有很大差异。

如何通过数学方法来确定收敛？

进行Automatic convergence test（自动收敛实验）。

例如：令 $ϵ\\epsilon$ 为 $10^{-3}$ ，在一次迭代中，如果 $J(w⃗,b)J(\\vec{w},b)$ 的下降值小于 $ϵ\\epsilon$ ，我们认为梯度下降收敛。

但是选定一个合适的 $ϵ\\epsilon$ 也是比较困难的，所以应当结合学习曲线，进行观察。

2.3.3 选择合适的学习率

当出现了下图中的情况时，我们认为可能是代码中有bug或者learning rate过大。这是因为当学习率过大时，w的修改也会变大，因此而造成代价不降反增。

我们可以将α设置为很小的数字，观察迭代过程中代价是否下降，如果此时依然会有波动，那就应该是代码中出现了bug。确定不存在bug后，再逐步增大α，以求更快速的梯度下降。

2.3.4 特征工程（Feature Engineering）

实际问题中的特征往往不只一个，而且我们应当为模型选择合适的特征值，并且对已有特征进行组合获得新的特征。

2.3.5 多项式回归（Polynomial Regression）

一次多项式
$fw⃗,b(x)=w1x+bf_{\\vec{w},b}(x) = w_1x+b$
二次多项式
$fw⃗,b(x)=w1x+w2x2+bf_{\\vec{w},b}(x) = w_1x+w_2x^2+b$
三次多项式
$fw⃗,b(x)=w1x+w2x2+w3x3+bf_{\\vec{w},b}(x) = w_1x+w_2x^2+w_3x^3+b$
二次方根多项式
$fw⃗,b(x)=w1x+w2x+bf_{\\vec{w},b}(x) = w_1x+w_2\\sqrt{x}+b$

2.4 Classification

2.4.1 Logistic Regression（逻辑回归）

【注】此部分内容在西瓜书上被写作“对数几率回归”

有很多现实问题的答案是“是”或者“否”，这样的问题我们称之为二元分类（binary classification）。对于二元分类问题，如果我们通过线性回归进行拟合，就会产生误差。

比如在恶性肿瘤分类的问题中，如果已经进行了拟合，现加入新的坐标点，就可能会出现错误分类。线性拟合显然已无法满足分类问题，我们通过逻辑回归来处理该类问题。

首先引入Sigmoid function（Sigmoid函数），也被称为logistic function（逻辑函数），显然Sigmoid函数的值域为0到1。

如果用 $g (z)$ 来表示这个函数，那么：
$g(z)=11+e−z,0<g(z)<1g(z)=\\frac{1}{1+e^{-z}},0<g(z)<1$

$Model:fw⃗,b(x⃗)=g(w⃗⋅x⃗+b)=11+e−(w⃗⋅x⃗+b)Model:f_{\\vec{w},b}(\\vec{x})=g(\\vec{w}·\\vec{x}+b)=\\frac{1}{1+e^{-(\\vec{w}·\\vec{x}+b)}}$
在恶行肿瘤判断案例中，x即为肿瘤大小，y为是否是恶性肿瘤的二元分类，如果一位病人的肿瘤根据计算为 $fw⃗,b(x⃗)=0.7f_{\\vec{w},b}(\\vec{x})=0.7$ ，我们就认为模型告诉我们这位病人的肿瘤有70%的概率为恶性的。

由于 $P (y = 0) + P (y = 1) = 1$ ，我们也可以说，这位病人的肿瘤有30%的概率为良性的。

有时会有这样的描述，这个式子表示，在给定输入特征的前提下（x为输入，w和b为参数），y等于1的概率是多少（条件概率）。
$fw⃗,b(x⃗)=P(y=1∣x⃗;w⃗,b)f_{\\vec{w},b}(\\vec{x})=P(y=1|\\vec{x};\\vec{w},b)$

2.4.2 Decision Boundary（决策边界）

根据Sigmoid函数，我们获得了新模型来描述逻辑回归模型：
$fw⃗,b(x⃗)=g(w⃗⋅x⃗+b)=11+e−(w⃗⋅x⃗+b)=P(y=1∣x⃗;w⃗,b)f_{\\vec{w},b}(\\vec{x})=g(\\vec{w}·\\vec{x}+b)=\\frac{1}{1+e^{-(\\vec{w}·\\vec{x}+b)}}=P(y=1|\\vec{x};\\vec{w},b)$
当 $fw⃗,b(x⃗)>=0.5f_{\\vec{w},b}(\\vec{x})>=0.5$ ，我们认为 $y^=1\\hat{y}=1$ ；当 $fw⃗,b(x⃗)<0.5f_{\\vec{w},b}(\\vec{x})<0.5$ ，我们认为 $y^=0\\hat{y}=0$ 。所以，什么情况下有 $fw⃗,b(x⃗)>=0.5f_{\\vec{w},b}(\\vec{x})>=0.5$ ?
$fw⃗,b(x⃗)>=0.5=>g(z)>=0.5=>z>=0=>w⃗⋅x⃗+b>=0<=>y^=1\\begin{align} &f_{\\vec{w},b}(\\vec{x}) >= 0.5 \\\\ &=> \\quad g(z) >= 0.5 \\\\ &=> \\quad z >= 0 \\\\ &=> \\quad \\vec{w}·\\vec{x} + b >= 0 \\\\ &<=>\\quad \\hat{y} = 1 \\end{align}$

当 $w⃗⋅x⃗+b=0\\vec{w}·\\vec{x}+b=0$ 时，这条线就表示决策边界。下图分别为线性决策边界和非线性决策边界。

2.4.3 Cost Function

现有上述training set，应当如何选取w向量和b？

如果选取平方误差代价函数（Squared error cost function）： $J(w⃗,b)=1m∑i=1m12(fw⃗,b(x(i))−y(i))2J(\\vec{w},b) = \\frac{1}{m} \\sum_{i=1}^m \\frac{1}{2}(f_{\\vec{w},b}(x^{(i)}) - y^{(i)})^2$ 。那么线性回归模型和逻辑回归模型的代价函数图大概如下所示：

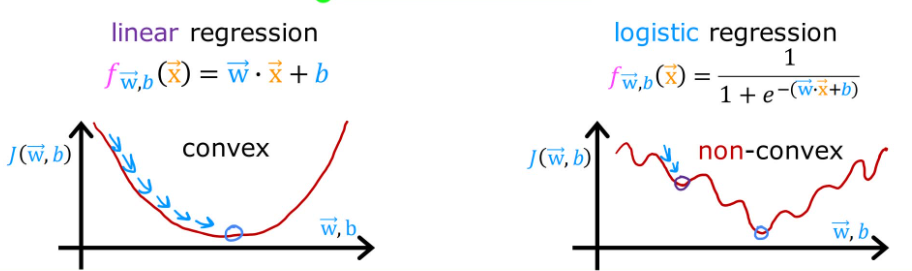
【机器学习学习笔记】机器学习入门监督学习

【convex】adj. 凸面的；n. 凸面

对于逻辑回归模型，平方误差代价函数显然不好，因为产生了很多局部极小值，这就使梯度下降过程中会卡在这些地方。所以应当构建一个新的函数，来让代价函数重新凸化。

我们修改一下代价函数 $J(w⃗,b)J(\\vec{w},b)$ 的定义：

我们把函数 $L(fw⃗,b(x(i)),y(i))L(f_{\\vec{w},b}(x^{(i)}) , y^{(i)})$ 称为单个训练例子的损失（the loss on a single training example），称之为损失函数
$KaTeX parse error: Expected 'EOF', got '&' at position 29: …oss \\ function:&̲ L(f_{\\vec{w},b…$

当 $y^{(i)}=1$ （即真实值为1）：

如果 $fw⃗,b(x⃗(i))f_{\\vec{w},b}(\\vec{x}^{(i)})$ 趋于1（即预测值趋于1），那么损失就趋于0，说明预测很准确
如果 $fw⃗,b(x⃗(i))f_{\\vec{w},b}(\\vec{x}^{(i)})$ 趋于0，那么损失就趋于无穷大
这就意味预测值离真实值越远，损失越大，反之越小

当 $y^{(i)}=0$ （即真实值为0）：

如果 $fw⃗,b(x⃗(i))f_{\\vec{w},b}(\\vec{x}^{(i)})$ 趋于0（即预测值趋于0），那么损失就趋于0，说明预测很准确
如果 $fw⃗,b(x⃗(i))f_{\\vec{w},b}(\\vec{x}^{(i)})$ 趋于1，那么损失就趋于无穷大

通过上文的叙述，我们归纳出针对逻辑回归的代价函数以及损失函数：
$J(w⃗,b)=1m∑i=1mL(fw⃗,b(x⃗(i)),y(i))L(fw⃗,b(x⃗(i)),y(i))={−log(fw⃗,b(x⃗(i))),ify(i)=1−log(1−fw⃗,b(x⃗(i))),ify(i)=0J(\\vec{w},b) = \\frac{1}{m} \\sum_{i=1}^m L(f_{\\vec{w},b}(\\vec{x}^{(i)}) , y^{(i)}) \\\\ \\\\ L(f_{\\vec{w},b}(\\vec{x}^{(i)}) , y^{(i)})= \\begin{cases} -log(f_{\\vec{w},b}(\\vec{x}^{(i)}))&,if\\ \\ y^{(i)}=1\\\\ -log(1-f_{\\vec{w},b}(\\vec{x}^{(i)}))&,if\\ \\ y^{(i)}=0 \\end{cases}$

之前针对线性回归的代价函数为：
$J(w⃗,b)=12m∑i=1m(fw⃗,b(x(i))−y(i))2J(\\vec{w},b) = \\frac{1}{2m} \\sum_{i=1}^m (f_{\\vec{w},b}(x^{(i)}) - y^{(i)})^2$

2.4.4 Simplified Cost Function

我们可以将上节中得出的分段损失函数改写为下式，通过简单分析就可以得出新式与原式是等价的。
$L(fw⃗,b(x⃗(i)),y(i))=−y(i)log(fw⃗,b(x⃗(i)))−(1−y(i))log(1−fw⃗,b(x⃗(i)))L(f_{\\vec{w},b}(\\vec{x}^{(i)}) , y^{(i)})= -y^{(i)}log(f_{\\vec{w},b}(\\vec{x}^{(i)})) -(1-y^{(i)})log(1-f_{\\vec{w},b}(\\vec{x}^{(i)}))$
于是简化后的代价函数就是：
$J(w⃗,b)=1m∑i=1m[L(fw⃗,b(x⃗(i)),y(i))]=−1m∑i=1m[y(i)log(fw⃗,b(x⃗(i)))+(1−y(i))log(1−fw⃗,b(x⃗(i)))]J(\\vec{w},b)= \\frac{1}{m} \\sum_{i=1}^m [L(f_{\\vec{w},b}(\\vec{x}^{(i)}) , y^{(i)})]= -\\frac{1}{m} \\sum_{i=1}^m [ y^{(i)}log(f_{\\vec{w},b}(\\vec{x}^{(i)})) +(1-y^{(i)})log(1-f_{\\vec{w},b}(\\vec{x}^{(i)})) ]$

2.4.5 Gradient Descent

$repeat{wj=wj−α∂∂wJ(w⃗,b)=wj−α[1m∑i=1m(fw⃗,b(x⃗(i))−y(i))xj(i)]b=b−α∂∂bJ(w⃗,b)=b−α[1m∑i=1m(fw⃗,b(x⃗(i))−y(i))]}simultaneousupdates\\begin{align} &repeat \\{ \\\\ &\\qquad w_j = w_j - α \\frac{∂}{∂w} J(\\vec{w},b) = w_j - α [ \\frac{1}{m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} ] \\\\ &\\qquad b = b - α \\frac{∂}{∂b} J(\\vec{w},b) = b - α [ \\frac{1}{m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)}) ] \\\\ &\\} simultaneous \\quad updates \\end{align}$

对于逻辑回归中的梯度下降参数，我们同样进行同步更新，上式中求偏导后的式子恰好与线性回归中式子相同，但他们的含义并不同。

这是因为在Linear regression中： $fw⃗,b(x⃗)=w⃗⋅x⃗+bf_{\\vec{w},b}(\\vec{x}) = \\vec{w} · \\vec{x} + b$ ；但是在Logistic regression中： $fw⃗,b(x⃗)=g(w⃗⋅x⃗+b)=11+e−(w⃗⋅x⃗+b)f_{\\vec{w},b}(\\vec{x}) = g(\\vec{w} · \\vec{x} + b) = \\frac{1}{1 + e^{-(\\vec{w} · \\vec{x} + b)}}$ ，但二者都可以进行梯度下降监视。

2.5 Underfitting and Overfitting

2.5.1 Summarize

在经典房价预测案例中，假定已获得上图中的数据，并将这些数据作为测试集进行拟合。

若选用一次多项式进行拟合，显然与趋势不同，因为当面积越来越大，房价也趋于平稳，不会像一次函数一样无限增长。我们称这样的结果为欠拟合（Underfitting）或高偏差（high bias）。

如果选用更高次项的多项式，得到的结果十分准确的拟合了数据集中的每一个训练数据，代价函数也几乎等于零。但这是一条很波动的曲线，有时当面积增加房价反而大幅下降，这显然也与实际不符。我们称这样的结果为过拟合（Overfitting）或高方差（high variance）。

欠拟合和过拟合的模型都不具备泛化（generalization）新样本的能力。

同理，对于逻辑回归模型，也有类似的拟合情况。上图是恶行肿瘤判断案例， $x_1$ 表示患者年龄， $x_2$ 表示肿瘤大小。

2.5.2 Addressing Overfitting

Collect more training examples

应对过拟合的方法之一就是搜集更多的测试数据，不断添加新的数据后，过拟合将逐步被解决。但如果无法获取足够多的测试数据，该方法就失效了。
Select features to include/exclude

造成过拟合的原因之一可能是选取的特征过多了，有时应当对特征进行舍弃，减少特征的数量也是解决过拟合的方法之一。但如果如此多的特征确实都是无法舍弃的，该方法就失效了。
Regularization

正则化是对特征的参数进行缩小，即减小某特征的权重，而非像方法二一样直接删除掉这个特征。即：保留所有特征，但防止权重过大造成过拟合。

2.5.3 Regularization（正则化）

以线性回归模型为例，其代价函数为 $J(w⃗,b)=12m∑i=1m(fw⃗,b(x⃗(i))−y(i))2J(\\vec{w},b) = \\frac{1}{2m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)})^2$ 。

当过度追求最小化代价函数，即 $minw⃗,b{J(w⃗,b)}=minw⃗,b{12m∑i=1m(fw⃗,b(x⃗(i))−y(i))2}\\underset{\\vec{w},b}{min} \\ \\{J(\\vec{w},b) \\} = \\underset{\\vec{w},b}{min} \\ \\{\\frac{1}{2m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)})^2\\}$ ，就会出现上文中过拟合的情况，显然过拟合时，代价函数的值要比“just right”时代价函数的值要小。所以应当优化代价函数的公式，不应该只考虑估计值与真实值的差距，也应当考虑不同多项式的权重。

比如当下右图中 $x^3,x^4$ 的系数 $w_3,w_4$ 趋于0时，拟合曲线就会更加平滑，接近下左图的情况。

现将代价函数修改为下式，1000为任意给定的一个较大的数字，旨在进行说明而非强制为1000。
$minw⃗,b{J(w⃗,b)}=minw⃗,b{12m∑i=1m(fw⃗,b(x⃗(i))−y(i))2+1000w32+1000w42}\\underset{\\vec{w},b}{min} \\{J(\\vec{w},b)\\} = \\underset{\\vec{w},b}{min} \\{ \\frac{1}{2m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)})^2 + 1000w_3^2 + 1000w_4^2 \\}$
此时，如果继续追求最小化代价函数， $w_3,w_4$ 也被纳入了考虑范围，并且越小越好。当得到最小化后的代价函数时，由于 $x^3,x^4$ 的系数 $w_3,w_4$ 趋于0（也称为：对 $w_3,w_4$ 进行了惩罚），图像更加趋于二次函数的样子，这样就大幅度消除了过拟合带来的影响，这就是正则化的思想。

但是正则化过程中我们往往无法直接确定哪个特征应当被惩罚，所以正则化的实现通常是惩罚所有特征，现在建立一个对所有特征都进行惩罚的模型，其中， $λ\\lambda$ 为正则化参数，对于参数b，是否进行惩罚带来的影响很小。
$minw⃗,b{J(w⃗,b)}=minw⃗,b{12m∑i=1m(fw⃗,b(x⃗(i))−y(i))2+λ2m∑j=1nwj2}\\underset{\\vec{w},b}{min} \\{J(\\vec{w},b)\\} = \\underset{\\vec{w},b}{min}\\{ \\frac{1}{2m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)})^2 + \\frac{\\lambda}{2m} \\sum_{j=1}^nw_j^2 \\}$
上式中第一项为均方误差代价（squared error cost），第二项为正则化项（regularization term）。

当 $λ\\lambda$ 取不同值时会有不同的惩罚效果，考虑两个极端情况，若 $λ=0\\lambda=0$ ，其实就是不进行惩罚，则可能会产生之前的过拟合现象；若 $λ=1\\lambda=1$ ，则对每一项都进行了极大的惩罚，这就使得模型变为： $fw⃗,b(x⃗)=bf_{\\vec{w},b}(\\vec{x}) = b$ ，也就产生了欠拟合情况。

2.5.4 线性回归模型的正则化

根据上文中给出的新模型，可以得出正则化后的梯度下降算法：
$repeat{wj=wj−α∂∂wjJ(w⃗,b)=wj−α[1m∑i=1m(fw⃗,b(x⃗(i))−y(i))xj(i)+λmwj]b=b−α∂∂bJ(w⃗,b)=b−α[1m∑i=1m(fw⃗,b(x⃗(i))−y(i))]}simultaneousupdatesandfw⃗,b(x⃗)=w⃗⋅x⃗+b\\begin{align} &repeat \\{ \\\\ &\\qquad w_j = w_j - α \\frac{∂}{∂w_j} J(\\vec{w},b) = w_j - α [ \\frac{1}{m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} + \\frac{\\lambda}{m}w_j ] \\\\ &\\qquad b = b - α \\frac{∂}{∂b} J(\\vec{w},b) = b - α [ \\frac{1}{m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)}) ] \\\\ &\\} simultaneous \\quad updates \\\\\\\\ &and \\quad f_{\\vec{w},b}(\\vec{x}) = \\vec{w} · \\vec{x} + b \\end{align}$
我们可以对上式中关于 $w_j$ 的式子进行简单化简：
$wj=wj−α[1m∑i=1m(fw⃗,b(x⃗(i))−y(i))xj(i)+λmwj]=wj−αλmwj−α1m∑i=1m(fw⃗,b(x⃗(i))−y(i))xj(i)=(1−αλm)wj−α1m∑i=1m(fw⃗,b(x⃗(i))−y(i))xj(i)\\begin{align} w_j &= w_j - α [ \\frac{1}{m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} + \\frac{\\lambda}{m}w_j ] \\\\ &= w_j - α \\frac{\\lambda}{m} w_j - α \\frac{1}{m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} \\\\ &= (1 - α \\frac{\\lambda}{m}) w_j - α \\frac{1}{m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} \\\\ \\end{align}$
对比之前得到的线性回归模型梯度下降算法中关于 $w_j$ 的式子：
$wj=wj−α1m∑i=1m(fw⃗,b(x⃗(i))−y(i))xj(i)w_j = w_j - α \\frac{1}{m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)}$
不难看出，正则化后的表达式与未正则化的表达式的不同之处在于：第一项之前乘了 $\\frac{\\lambda}{m})$ 。

$α\\alpha$ 是学习率，是一个很小的正数（0-1）， $λ\\lambda$ 是正则化参数，也是一个较小的正数（1-10），m表示一个训练集中的样本数量，通常较大，所以不难算出 $\\frac{\\lambda}{m})$ 是一个略微小于1的正数。

这其实就是正则化的工作原理：在每次迭代时主动减小一些 $w_j$ ，然后执行普通更新，所以才使得原本不收敛的学习路线图变得收敛。

2.5.5 逻辑回归模型的正则化

根据逻辑回归模型的代价函数以及前文得到的正则化方法，可以构建新的代价函数：
$J(w⃗,b)=−1m∑i=1m{y(i)log[fw⃗,b(x⃗(i))]+(1−y(i))log[1−fw⃗,b(x⃗(i))]}+λ2m∑j=1nwj2J(\\vec{w},b)= -\\frac{1}{m} \\sum_{i=1}^m \\{ \\ y^{(i)}log[f_{\\vec{w},b}(\\vec{x}^{(i)})] +(1-y^{(i)})log[1-f_{\\vec{w},b}(\\vec{x}^{(i)})] \\ \\} + \\frac{\\lambda}{2m} \\sum_{j=1}^nw_j^2$

同样可以得到下面的正则化后的逻辑回归模型的代价函数：
$repeat{wj=wj−α∂∂wjJ(w⃗,b)=(1−αλm)wj−α1m∑i=1m(fw⃗,b(x⃗(i))−y(i))xj(i)b=b−α∂∂bJ(w⃗,b)=b−α1m∑i=1m(fw⃗,b(x⃗(i))−y(i))}simultaneousupdatesandfw⃗,b(x⃗)=g(w⃗⋅x⃗+b)=11+e−(w⃗⋅x⃗+b)\\begin{align} &repeat \\{ \\\\ &\\qquad w_j = w_j - α \\frac{∂}{∂w_j} J(\\vec{w},b) = (1 - α \\frac{\\lambda}{m}) w_j - α \\frac{1}{m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)}) x_j^{(i)} \\\\ &\\qquad b = b - α \\frac{∂}{∂b} J(\\vec{w},b) = b - α \\frac{1}{m} \\sum_{i=1}^m (f_{\\vec{w},b}(\\vec{x}^{(i)}) - y^{(i)}) \\\\ &\\} simultaneous \\quad updates \\\\\\\\ &and \\quad f_{\\vec{w},b}(\\vec{x}) = g(\\vec{w} · \\vec{x} + b) = \\frac{1}{1 + e^{-(\\vec{w} · \\vec{x} + b)}} \\end{align}$

【机器学习学习笔记】机器学习入门监督学习

1. 机器学习入门

1.1 What is Machine Learning?

1.2 Supervised learning

1.3 Unsupervised learning

2. Supervised learning