👦个人主页：@Weraphael
✍🏻作者简介：目前学习C++和算法
✈️专栏：数据结构
🐋 希望大家多多支持，咱一起进步！😁
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注✨

【本章内容】

一、栈

1.1 概念

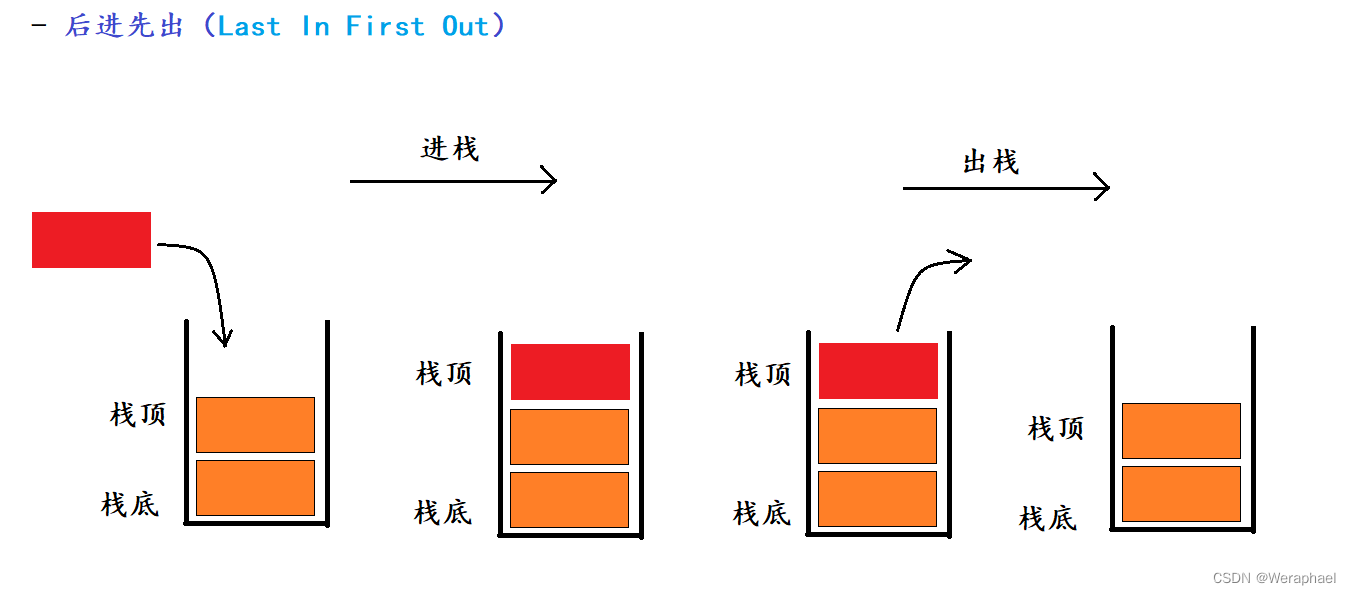
• 栈是一种特殊的线性表，只允许在固定的一端进行插入和删除元素的操作。其中进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的元素遵守后进先出LIFO(Last In First Out)的原则。
• 压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
• 出栈：栈的删除操作叫做出栈，出数据也是在栈顶。
  

1.2 栈的结构

栈的实现既可以使用顺序表实现，也可以用链表实现。但是，栈使用顺序表实现会比链表实现更有优势。因为栈是后进（栈顶进）的先出（栈顶出），实现一个栈需要尾插和尾删，而顺序表的尾插和尾删效率高，它的时间复杂度都是O(1)，而单链表的尾插和尾删比顺序表低，它的时间复杂度是O(n)
对于顺序表大家可以看看这边博客 —> 点击跳转

【结构】

typedef struct Stack
{int* a;  	//指向动态开辟的数组int top; 	//表示栈顶int capacity;//容量空间的大小
}Stack;

1.3 准备工作

为了方便管理，我们可以创建多个文件来实现
test.c - 测试代码逻辑 （源文件）
stack.c - 动态的实现 （源文件）
stack.h - 存放函数的声明 （头文件）

1.4 常见接口

【stack.h】

typedef struct Stack
{int* a;int top;int capacity;
}Stack;//栈的初始化
void STInit(Stack* ps);//栈的销毁
void STDestroy(Stack* ps);//栈的尾插
void STPush(Stack* ps, int x);//栈的尾删
void STPop(Stack* ps);//栈的大小
int STSize(Stack* ps);//栈是否为空
bool STEmpty(Stack* ps);//栈顶元素
int STTop(Stack* ps);

1.5 代码实现之栈的初始化

【stack.c】

//栈的初始化
void STInit(Stack* ps)
{assert(ps);ps->a = (int*)malloc(sizeof(int) * 4);if (ps->a == NULL){perror("ps->a :: malloc");return;}ps->top = 0;ps->capacity = 4;
}

• 详细细节参考这篇博客： 点击跳转

1.6 代码实现之栈的销毁

【stack.c】

//栈的销毁
void STDestroy(Stack* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->capacity = 0;ps->top = 0;
}

• 详细细节参考这篇博客： 点击跳转

1.7 代码实现之栈的尾插

【stack.c】

//栈的尾插
void STPush(Stack* ps, int x)
{assert(ps);//判断是否需要扩容if (ps->top == ps->capacity){int* tmp = (int*)realloc(ps->a, sizeof(int) * ps->capacity * 2);if (tmp == NULL){perror("tmp :: realloc");return;}ps->capacity *= 2;ps->a = tmp;tmp = NULL;}//尾插ps->a[ps->top] = x;ps->top++;
}

• 详细细节参考这篇博客： 点击跳转

1.8 代码实现之栈的尾删

【stack.c】

//栈的尾删
void STPop(Stack* ps)
{assert(ps);//特判顺序表为空的情况assert(!STEmpty(ps));ps->top--;
}

• 详细细节参考这篇博客： 点击跳转

1.9 代码实现之栈的大小

【stack.c】

//栈的大小
int STSize(Stack* ps)
{assert(ps);return ps->top;
}

【学习笔记】
一开始初始化栈顶top为 0，表示栈尾插后，top会指向栈顶的下一个元素。因此top就代表整个栈的大小。

1.9 代码实现之判断栈是否为空

【stack.c】

//栈是否为空
bool STEmpty(Stack* ps)
{assert(ps);return ps->top == 0;
}

1.10 代码实现之返回栈顶元素

【stack.c】

//栈顶元素
int STTop(Stack* ps)
{assert(ps);//当ps->top 为 0时，会导致越界assert(ps->top != 0);//assert(!STEmpty(ps));return ps->a[ps->top - 1];
}

1.11 test.c

#include "stack.h"int main()
{Stack st;STInit(&st);STPush(&st, 1);STPush(&st, 2);STPush(&st, 3);STPush(&st, 4);//注意：栈不能直接打印，因为它在途中出数据while (!STEmpty(&st)){printf("%d ", STTop(&st));STPop(&st);}STDestroy(&st);return 0;
}

二、队列

2.1 概念

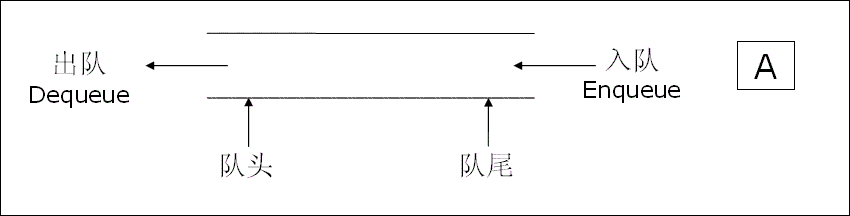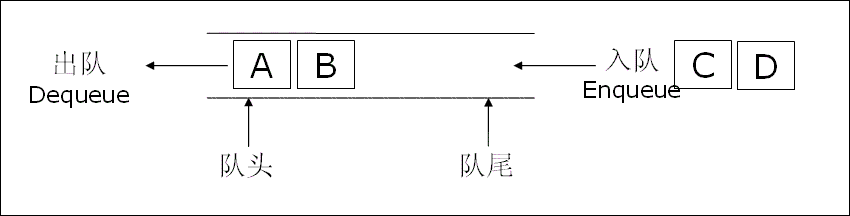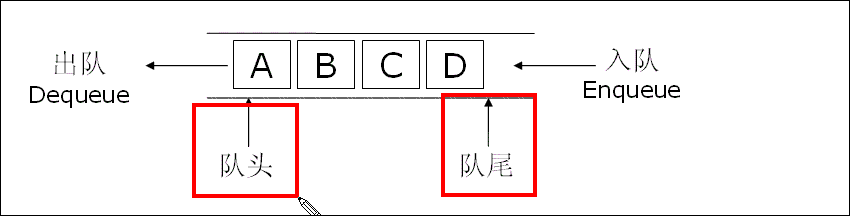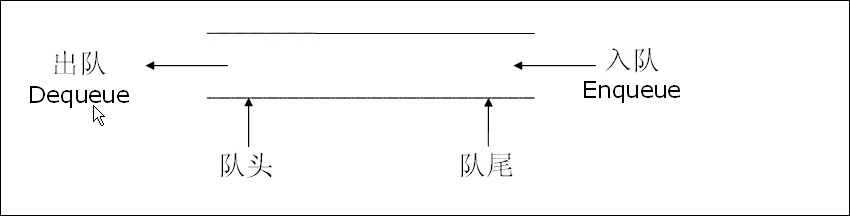
• 只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表
• 队列具有先进先出FIFO(First In First Out)
• 入队列：进行插入操作的一端称为队尾
  出队列：进行删除操作的一端称为队头

2.2 队列的结构

首先队列也可以用顺序表和链表的结构实现，但是，使用链表实现会更优一些，为什么呢？

答：首先队列是先进先出的，并且它需要尾插和头删。所以，对于顺序表来说，尾删是比单链表快很多，但其头删却要移动整个数据，就显得非常麻烦。而对于单链表来说，头删是非常easy的，而尾插需要遍历，时间复杂度是O（n）

【结构】

typedef struct QNode
{struct QNode* next;int data;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;

大家可能会有点奇怪，为什么在单链表章节不定义一个首尾指针结构体？
答案是：因为队列需要尾插而不需要尾删，什么意思呢？对于普通单链表来说，在尾删之前是需要记录尾节点的前一个节点的，即使在单链表上定义一个首尾指针结构体，但时候尾删还是得遍历一遍链表来找到尾节点的前一个结点，因此普通单链表再定义一个首尾指针结构体有点白费力气，而队列不同，它只进行头删和尾插的操作。

2.3 准备工作

为了方便管理，我们可以创建多个文件来实现
test.c - 测试代码逻辑 （源文件）
Queue.c - 动态的实现 （源文件）
Queue.h - 存放函数的声明 （头文件）

1.4 常见接口

【Queue.h】

typedef struct QNode
{struct QNode* next;int data;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;int size; // 队列大小
}Queue;//头指针和尾指针的初始化
void QueueInit(Queue* pq);//开辟内存空间的销毁
void QueueDestroy(Queue* pq);//队列的尾插
void QueuePush(Queue* pq, int x);//队列的头删
void QueuePop(Queue* pq);//队列的大小
int QueueSize(Queue* pq);//判断队列是否为空
bool QueueEmpty(Queue* pq);//队头数据
int QueueFront(Queue* pq);//队尾数据
int QueueBack(Queue* pq);

1.5 队列之头尾指针初始化

//头指针和尾指针的初始化
void QueueInit(Queue* pq)
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}

【笔记总结】

1. 断言问题。pq是一个结构体指针，指向一个首尾指针的结构体，pq指向NULL，这个队列就没法玩了
   

1.5 队列之内存空间的销毁

//开辟内存空间的销毁
void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){//在删除当前节点前记录下一个节点QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;pq->size = 0;
}

1.6 队列之尾插

//队列的尾插
void QueuePush(Queue* pq, int x)
{assert(pq);//尾插的第一步，先向内存申请空间QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("newnode :: malloc");return;}//再对newnode初始化newnode->data = x;newnode->next = NULL;//接下来开始尾插//第一个问题：当前的链表可能为空if (pq->head == NULL){//在链表为空的情况下tail，也一定为空（特判）//若tail不为空就是传错了assert(pq->tail == NULL);//直接赋值即可pq->head = pq->tail = newnode;}//否则就是正常的尾插else{//tail newnodepq->tail->next = newnode;pq->tail = newnode; //更新tail}//尾插后size个数+1pq->size++;
}

1.7 队列之头删

//队列的头删
void QueuePop(Queue* pq)
{assert(pq);//空链表是不能头删的assert(pq->head != NULL);//头删的特殊情况：链表中只有一个节点if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}//接下来就是正常的头删else{//记录头节点的下一个节点QNode* next = pq->head->next;free(pq->head);pq->head = next;}//删掉一个元素，队列的个数就要减1pq->size--;
}

1.8 队列之求队列大小

//队列的大小
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}

1.9 队列之判断队列是否为空

//判断队列是否为空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}

1.10 队列之求队头元素

//队头数据
int QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}

1.11 队列之求队尾元素

//队尾数据
int QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}

1.12 test.c部分

#include "Queue.h"int main()
{Queue node;QueueInit(&node);//入队列（尾插）QueuePush(&node, 1);QueuePush(&node, 2);QueuePush(&node, 3);QueuePush(&node, 4);//注意：队列不能直接打印，因为它在途中出数据while (!QueueEmpty(&node)){printf("%d ", QueueFront(&node));QueuePop(&node);}printf("\\n");QueueDestroy(&node);return 0;
}