23 - x的平方根，快速幂，超级次方

1. x的平方根

二分查找

class Solution {
public:int mySqrt(int x) {int left = 1, right = x;while(left <= right){int mid = left + (right - left) / 2;if(mid > x / mid){right = mid - 1;}else if(mid < x / mid){left = mid + 1;}else if(mid == x / mid){return mid;}}return right;}
};

2. 快速幂

• 二分法

每次把n缩小一半

class Solution {
public:double myPow(double x, int n) {if(n == 0) return 1;if(n == 1) return x;if(n == -1) return 1.0 / x;double v = myPow(x, n / 2);v *= v;if(n < 0 && n % 2){v = 1.0 / x * v;}if(n > 0 && n % 2){v = v * x;}return v;}
};

• 二进制快速幂

比如我们计算pow(3,5)，将5改写成二进制101，我们可以将算法过程写成以下形式：

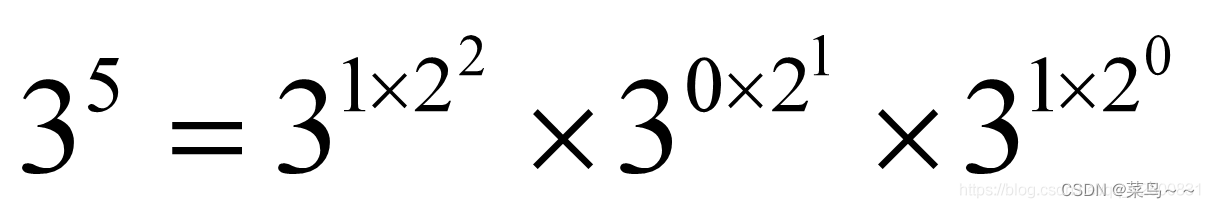
class Solution {
public:double myPow(double x, int n) {double res = 1;long long b = n;if(n < 0){x = 1 / x;b = -b; //直接把int的负数取反会溢出，由于b的值只有int范围，所以不会溢出}while(b){//当前位为1时，需要把这时的X计入结果if(b & 1){res *= x;}x *= x;//构造下一个乘积项：3^1,3^2,3^4,3^8,...b >>= 1;}return res;}
};

3. 超级次方

采用倒序遍历

class Solution {
public:int pow(int x, int n){int ans = 1;while(n){if(n % 2){ans = (long)ans * x % 1337;}x = (long)x * x % 1337;n >>= 1;}return ans;}int superPow(int a, vector<int>& b) {int result = 1;for(int i = b.size() - 1; i >= 0; --i){result = (long)result * pow(a, b[i]) % 1337;a = pow(a, 10);}return result;}
};