多分类、正则化问题

多分类问题
利用逻辑回归解决多分类问题,假如有一个训练集,有 3 个类别,分别为三角形 𝑦 = 1,方框𝑦 = 2,圆圈 𝑦 = 3。我们下面要做的就是使用一个训练集,将其分成 3 个二元分类问题。
我们先从用三角形代表的类别 1 开始,此时创造一个新的训练集,三角形为正类,方框和圆圈为负类;
对于方框代表的类别2,此时创造一个新的训练集,方框为正类,三角形和圆圈为负类;
对于圆圈代表的类别3,此时创造一个新的训练集,圆圈为正类,方框和三角形为负类。
过拟合问题
如果模型有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为 0),但是可能会不能推广到新的数据集。
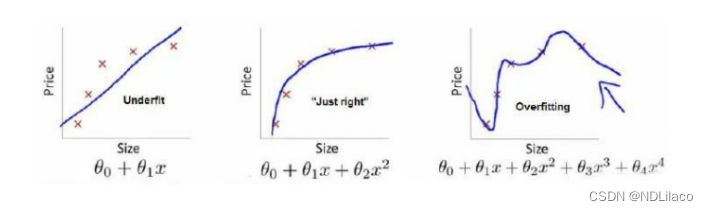
第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集;第三个模型是一
个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据。我们可以看
出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的
训练集但在新输入变量进行预测时可能会效果不好;而中间的模型似乎最合适。
过拟合问题解决方法:
1.丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如 PCA)
2.正则化。 保留所有的特征,但是减少参数的大小(magnitude)。
正则化线性回归
对于上面的图片所示模型,由于高次项导致过拟合的问题,所以通过将高次项的系数接近于0来解决这个问题(即减少θ3、θ4\\theta_3、\\theta_4θ3、θ4的大小)。通过在θ3、θ4\\theta_3、\\theta_4θ3、θ4加入惩罚项来减少θ3、θ4\\theta_3、\\theta_4θ3、θ4的大小。
J(θ0,θ1,...,θn)=12m∑i=1m(hθ(x(i))−y(i))2J(\\theta_{0},\\theta_{1},...,\\theta_{n})=\\frac{1}{2m}\\sum_{i=1}^{m}{(h_{\\theta}(x^{(i)})-y^{(i)})^2} J(θ0,θ1,...,θn)=2m1i=1∑m(hθ(x(i))−y(i))2
将上述代价函数改为
J(θ0,θ1,...,θ4)=12m[∑i=1m(hθ(x(i))−y(i))2+1000θ32+10000θ42]J(\\theta_{0},\\theta_{1},...,\\theta_{4})=\\frac{1}{2m}[\\sum_{i=1}^{m}{(h_{\\theta}(x^{(i)})-y^{(i)})^2}+1000\\theta_3^2+10000\\theta_4^2] J(θ0,θ1,...,θ4)=2m1[i=1∑m(hθ(x(i))−y(i))2+1000θ32+10000θ42]
假如我们有非常多的特征,我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚,并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设(一般不对θ0\\theta_0θ0进行惩罚):
J(θ)=12m[∑i=1m(hθ(x(i))−y(i))2+λ∑j=1nθj2]J(\\theta)=\\frac{1}{2m}[\\sum_{i=1}^{m}{(h_{\\theta}(x^{(i)})-y^{(i)})^2}+\\lambda \\sum_{j=1}^{n} \\theta_j^2] J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
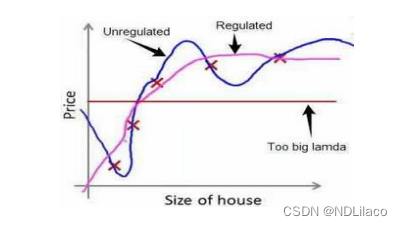
如果选择的正则化参数 λ 过大,则会把所有的参数都最小化了,导致模型变成 Font metrics not found for font: .,也就是图中红色直线所示的情况,造成欠拟合。 因为如果我们令 𝜆 的值很大的话,为了使 Cost Function 尽可能的小,所有的 𝜃 的值(不包括θ0\\theta_0θ0)都会在一定程度上减小。
对正则化后的代价函数进行梯度下降得到
θ0:=θ0−α1m∑i=1m(hθ(x(i))−y(i))x0(i)\\theta_0:=\\theta_0-\\alpha \\frac{1}{m}\\sum_{i=1}^{m}{(h_{\\theta}(x^{(i)})-y^{(i)})}x_0^{(i)} θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i)
θj:=θj−α[1m∑i=1m(hθ(x(i))−y(i))xj(i)+λmθj]\\theta_j:=\\theta_j-\\alpha[ \\frac{1}{m}\\sum_{i=1}^{m}{(h_{\\theta}(x^{(i)})-y^{(i)})}x_j^{(i)}+\\frac{\\lambda}{m} \\theta_j] θj:=θj−α[m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]
整个公式可写为
θj:=θj(1−αλm)−α1m∑i=1m(hθ(x(i))−y(i))xj(i)\\theta_j:=\\theta_j(1-\\alpha \\frac{\\lambda}{m})-\\alpha \\frac{1}{m}\\sum_{i=1}^{m}{(h_{\\theta}(x^{(i)})-y^{(i)})}x_j^{(i)} θj:=θj(1−αmλ)−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令𝜃值减少了一个额外的值。
利用正规方程来求解正则化线性回归模型
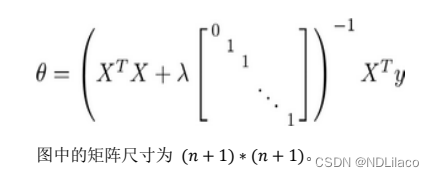
正则化逻辑回归模型
J(θ)=1m∑i=1m−y(i)⋅log(hθ(x(i)))−(1−y(i))⋅log(1−hθ(x(i)))+λ2m∑j=1nθj2J({\\theta})=\\frac{1}{m}\\sum_{i=1}^{m}{-y^{(i)}\\cdot log(h_{\\theta}(x^{(i)}))-(1-y^{(i)})\\cdot log(1-h_{\\theta}(x^{(i)}))}+\\frac{\\lambda}{2m}\\sum_{j=1}^{n} \\theta_j^2 J(θ)=m1i=1∑m−y(i)⋅log(hθ(x(i)))−(1−y(i))⋅log(1−hθ(x(i)))+2mλj=1∑nθj2
该代价函数的梯度下降算法为
θ0:=θ0−α1m∑i=1m(hθ(x(i))−y(i))x0(i)\\theta_0:=\\theta_0-\\alpha \\frac{1}{m}\\sum_{i=1}^{m}{(h_{\\theta}(x^{(i)})-y^{(i)})}x_0^{(i)} θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i)
θj:=θj−α[1m∑i=1m(hθ(x(i))−y(i))xj(i)+λmθj]\\theta_j:=\\theta_j-\\alpha[ \\frac{1}{m}\\sum_{i=1}^{m}{(h_{\\theta}(x^{(i)})-y^{(i)})}x_j^{(i)}+\\frac{\\lambda}{m} \\theta_j] θj:=θj−α[m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]


