一：线性回归基本概念

（1）回归分析

回归分析：回归分析是统计学中的基本概念，是指一种预测性的建模技术，主要研究自变量和因变量的关系，通常使用曲线拟合数据点，然后研究如何使曲线到数据点的距离差异最小

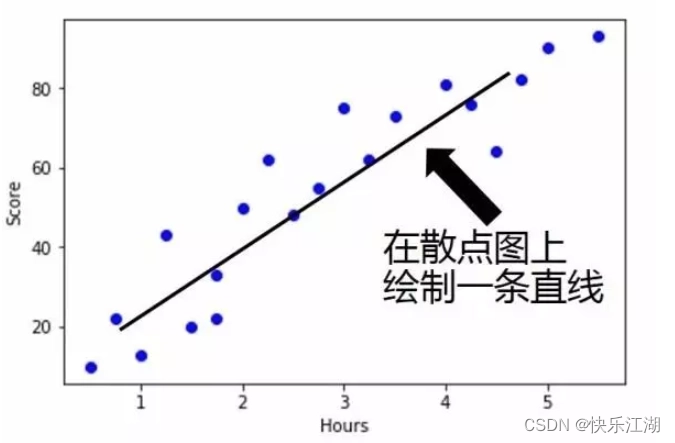
（2）线性回归

• 以一元线性回归为例（只有一个未知自变量）

线性回归：假设有$n$组数据，自变量x(x1,x2,...,xn)x(x_{1},x_{2},...,x_{n})x(x1​,x2​,...,xn​)，因变量y(y1,y2,...,yn)y(y_{1},y_{2},...,y_{n})y(y1​,y2​,...,yn​)，并且它们满足$f(x)=ax+b$，那么线性回归的目标就是如何能让$f(x)$和$y$之间的差异最小。其中衡量差异的方式即损失函数有很多种，在线性回归中主要使用均方误差，记$J(a,b)$为$f(x)$和$y$之间的差异，则：

J(a,b)=∑i=1n(f(x(i))−y(i))2=∑i=1n(ax(i)+b−y(i))2J(a, b)=\\sum\\limits_{i=1}^{n}(f(x^{(i)})-y^{(i)})^{2}=\\sum\\limits_{i=1}^{n}(ax^{(i)}+b-y^{(i)})^{2}J(a,b)=i=1∑n​(f(x(i))−y(i))2=i=1∑n​(ax(i)+b−y(i))2

可以发现$J(a,b)$是一个二次函数，所以有最小值，因此当$J(a,b)$取最小值时，$f(x)$和$y$的差异最小，所以关键在于确定$a$和$b$的值，方法有三种

• 最小二乘法
• 梯度下降法
• 正规方程

二：线性回归确定参数的方法

那也就是说最小二乘法、极大似然估计和梯度下降法它们虽然方法不同的，但是目的都是一样的，都是为了求解线性回归的参数？

（1）最小二乘法

A：代数求法

• 最小二乘法有代数求解和矩阵求解两种方法

分别关于$a$和$b$对函数J(a,b)=∑i=1n(f(x(i))−y(i))2=∑i=1n(ax(i)+b−y(i))2J(a, b)=\\sum\\limits_{i=1}^{n}(f(x^{(i)})-y^{(i)})^{2}=\\sum\\limits_{i=1}^{n}(ax^{(i)}+b-y^{(i)})^{2}J(a,b)=i=1∑n​(f(x(i))−y(i))2=i=1∑n​(ax(i)+b−y(i))2求偏导，然后令其为0解出$a$和$b$，解得

a=∑i=1ny(i)(x(i)−x‾)∑i=1n(x(i))2−1n(∑i=1nx(i))2a=\\frac{\\sum\\limits_{i=1}^{n}y^{(i)}(x^{(i)}-\\overline{x})}{\\sum\\limits_{i=1}^{n}(x^{(i)})^{2}-\\frac{1}{n}(\\sum\\limits_{i=1}^{n}x^{(i)})^{2}}a=i=1∑n​(x(i))2−n1​(i=1∑n​x(i))2i=1∑n​y(i)(x(i)−x)​

b=1n∑i=1n(y(i)−ax(i))b=\\frac{1}{n}\\sum\\limits_{i=1}^{n}(y^{(i)}-ax^{(i)})b=n1​i=1∑n​(y(i)−ax(i))

B：矩阵求法（主要使用）

假设函数hθ(x1,x2,...,xn=θ0+θ1x1+...+θn−1xn−1h_{\\theta}(x_{1}, x_{2}, ... , x_{n}=\\theta_{0}+\\theta_{1}x_{1}+...+\\theta_{n-1}x_{n-1}hθ​(x1​,x2​,...,xn​=θ0​+θ1​x1​+...+θn−1​xn−1​的矩阵表达式为

hθ(x)=Xθh_{\\theta}(x)=X\\thetahθ​(x)=Xθ

• $X$为$m\times n$维矩阵，其中$m$代表样本个数，$n$代表样本特征数
• hθ(x)h_{\\theta}(x)hθ​(x)为$m\times 1$向量，$\theta$为$n\times 1$向量

损失函数定义为

J(θ)=12(Xθ−Y)T(Xθ−Y)J(\\theta)=\\frac{1}{2}(X\\theta-Y)^{T}(X\\theta-Y)J(θ)=21​(Xθ−Y)T(Xθ−Y)

• $Y$是样本的输出向量，维度为$m\times 1$
• 12\\frac{1}{2}21​主要是为了求导后系数为1

接下来需要对$\theta$向量求导并令其为0

∂∂θJ(θ)=XT(Xθ−Y)=0\\frac{\\partial}{\\partial \\theta}J(\\theta)=X^{T}(X\\theta-Y)=0∂θ∂​J(θ)=XT(Xθ−Y)=0

解得

θ=(XTX)−1XTY\\theta = (X^{T}X)^{-1}X^{T}Yθ=(XTX)−1XTY

（2）极大似然估计

A：极大似然估计

极大似然估计是一种用于估计概率分布参数的统计方法。假设有一随机变量$X$，其概率密度函数为$f(x;\theta )$，其中$\theta$是一个定义分布的参数向量。极大似然估计的目标是，对于一给定的数据集x1,x2,...xnx_{1},x_{2},...x_{n}x1​,x2​,...xn​找到使似然函数$L(\theta |x)$最大化的$\theta$值

L(θ∣x)=f(x1;θ)∗f(x2;θ)∗...∗f(xn;θ)L(\\theta|x)=f(x_{1};\\theta)*f(x_{2};\\theta)*...*f(x_{n};\\theta) L(θ∣x)=f(x1​;θ)∗f(x2​;θ)∗...∗f(xn​;θ)

似然函数是指在给定的$\theta$值下观察到给定数据x1,x2,...xnx_{1},x_{2},...x_{n}x1​,x2​,...xn​的概率极大似然估计意味着找到使观察到的数据最可能出现的参数$\theta$。在数学上，我们可以将$\theta$的极大似然估计表示为

$$argmax=(L(\theta |x))$$

这意味着我们需要找到使似然函数最大化的$\theta$值。在实际使用时，使用对数似然函数$\log (L(\theta |x))$往往更容易，因为它是似然的单调函数，具有相同的最大值。对数似然函数定义为：

log⁡(L(θ∣x))=log⁡(f(x1;θ))+log⁡(f(x2;θ))+...+log⁡(f(xn;θ))\\log(L(\\theta|x))=\\log(f(x_{1};\\theta))+\\log(f(x_{2};\\theta))+...+\\log(f(x_{n};\\theta)) log(L(θ∣x))=log(f(x1​;θ))+log(f(x2​;θ))+...+log(f(xn​;θ))

一旦我们有了对数似然函数，我们就可以使用梯度下降法等优化方法来寻找$\theta$的极大似然估计

B：极大似然估计求解线性回归

假设我们有一堆输入和输出组成的数据集，表示为(x1,y1),(x2,y2),…,(xn,yn){(x_1, y_1), (x_2, y_2), \\ldots, (x_n, y_n)}(x1​,y1​),(x2​,y2​),…,(xn​,yn​)，我们假设输入和输出之间存在着线性关系，由方程$y=mx+b$给出。我们的目标是找到可以最佳拟合数据的$m$和$b$

为了使用极大似然估计，我们做出以下假设

• 预测值y^\\hat{{y}}y^​和真实值$y$之间的误差满足正态分布（均值为0，方差为σ2\\sigma^2σ2）
• 误差是独立同分布的

基于这些假设，似然函数可以写成下面这样

• 其中y^i=mxi+b\\hat{y}_i = mx_i + by^​i​=mxi​+b是yiy_iyi​的预测值

L(m,b∣{xi,yi})=∏i=1n12πσ2exp⁡(−(yi−yi^)22σ2)L(m,b|\\{x_{i},y_{i}\\})=\\prod_{i=1}^{n}\\frac{1}{\\sqrt{ 2\\pi \\sigma^{2} }}\\exp(-\\frac{(y_{i}-\\hat{y_{i}})^{2}}{2\\sigma^{2}}) L(m,b∣{xi​,yi​})=i=1∏n​2πσ2​1​exp(−2σ2(yi​−yi​^​)2​)
取似然函数的负对数，我们就得到了负对数似然函数

−ln⁡L(m,b∣{xi,yi})=n2ln⁡(2πσ2)+12σ2∑i=1n(yi−mxi−b)2-\\ln L(m,b|\\{x_{i},y_{i}\\})=\\frac{n}{2}\\ln(2\\pi \\sigma^{2})+\\frac{1}{2\\sigma^{2}}\\sum_{i=1}^{n}(y_{i}-mx_{i}-b)^{2} −lnL(m,b∣{xi​,yi​})=2n​ln(2πσ2)+2σ21​i=1∑n​(yi​−mxi​−b)2

我们的目标是找到最小化负对数似然函数的$m$和$b$的值。这可以用梯度下降法来完成，这涉及到迭代更新$m$和$b$的值，直到收敛

• 下面介绍梯度下降

（3）梯度下降

A：梯度

梯度：对多元函数的各参数求偏导，然后把求得的各个参数的偏导数以向量的形式写出来，就是梯度

• 注意：当函数是一元函数，梯度就是导数

• 例如函数$f(x,y)$分别对$x$和$y$求偏导数，求得的梯度向量就是(∂f∂x,∂f∂y)(\\frac{\\partial f}{\\partial x}, \\frac{\\partial f}{\\partial y})(∂x∂f​,∂y∂f​)，简写为$gradf(x,y)$

从几何意义上来讲，梯度向量就是函数变化最快的的地方，沿着梯度向量的方向，更容易找到函数的最大值，同理沿着梯度向量相反的方向，更容易找到函数的最小值

B：梯度下降算法简介

梯度下降算法：假设有$n$组数据，自变量x(x1,x2,...,xn)x(x_{1},x_{2},...,x_{n})x(x1​,x2​,...,xn​)，因变量y(y1,y2,...,yn)y(y_{1},y_{2},...,y_{n})y(y1​,y2​,...,yn​)，并且它们满足$f(x)=ax$，记$J(a)$为$f(x)$和$y$之间的差异，也即

J(a,)=∑i=1n(f(x(i))−y(i))2=∑i=1n(ax(i)−y(i))2J(a,)=\\sum\\limits_{i=1}^{n}(f(x^{(i)})-y^{(i)})^{2}=\\sum\\limits_{i=1}^{n}(ax^{(i)}-y^{(i)})^{2}J(a,)=i=1∑n​(f(x(i))−y(i))2=i=1∑n​(ax(i)−y(i))2

在梯度下降算法中，需要给参数$a$给一个预设值，然后逐步修改$a$，直到$J(a)$取到最小值时，确定$a$的值。梯度下降公式如下

repeat{a:=a−α∂J(a)∂a}repeat\\{a := a-\\alpha \\frac{\\partial J(a)}{\\partial a}\\}repeat{a:=a−α∂a∂J(a)​}

类比于生活中下山的例子，当一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处

可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解

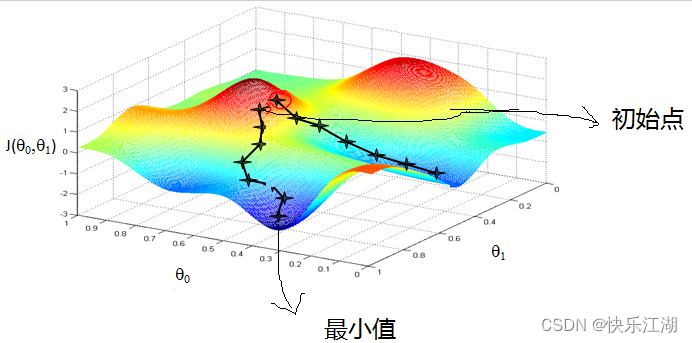
C：梯度下降算法代数描述

①：先决条件：确认优化模型的假设函数和损失函数

• 对于线性回归，假设函数表示为hθ(x1,x2,..,xn)=θ0+θ1x1+...+θnxn∣h_{\\theta}(x_{1},x_{2},..,x_{n})=\\theta_{0}+\\theta_{1}x_{1}+...+\\theta_{n}x_{n}|hθ​(x1​,x2​,..,xn​)=θ0​+θ1​x1​+...+θn​xn​∣，为了简化我们可以增加一个特征x0=1x_{0}=1x0​=1，这样hθ(x0,x1,...,xn)=∑i=0nθixih_{\\theta}(x_{0},x_{1},...,x_{n})=\\sum\\limits_{i=0}^{n}\\theta_{i}x_{i}hθ​(x0​,x1​,...,xn​)=i=0∑n​θi​xi​
• 对于上面的假设函数，其损失函数为J(θ0,θ1,...,θn)=12m∑j=1n(hθ(x0j,x1j,...,xnj)−yj)J(\\theta_{0},\\theta_{1},...,\\theta_{n})=\\frac{1}{2m}\\sum\\limits_{j=1}^{n}(h_{\\theta}(x_{0}^{j},x_{1}^{j},...,x_{n}^{j})-y_{j})J(θ0​,θ1​,...,θn​)=2m1​j=1∑n​(hθ​(x0j​,x1j​,...,xnj​)−yj​)

②：算法参数初始化：主要是初始化θ0,θ1,...,θn\\theta_{0},\\theta_{1},...,\\theta_{n}θ0​,θ1​,...,θn​、算法终止距离$\xi$和步长$\alpha$

• 在没有任何先验知识的情况下，可以将所有的$\theta$初始化为0，将步长初始化为1

③：算法流程：

• 确定当前位置的损失函数梯度：对于θi\\theta_{i}θi​其梯度表达式为∂∂θiJ(θ0,θ1,...,θn)\\frac{\\partial}{\\partial \\theta_{i}}J(\\theta_{0},\\theta_{1},...,\\theta_{n})∂θi​∂​J(θ0​,θ1​,...,θn​)
• 用步长乘以损失函数的梯度，得到当前位置下降距离： 也即α∂∂θiJ(θ0,θ1,...,θn)\\alpha \\frac{\\partial}{\\partial \\theta_{i}}J(\\theta_{0},\\theta_{1},...,\\theta_{n})α∂θi​∂​J(θ0​,θ1​,...,θn​)
• 确定是否所有的θi\\theta_{i}θi​梯度下降距离都小于$\xi$，若小于则算法终止，当前所有的θi\\theta_{i}θi​即为最终结果，否则转入下一步
• 更新所有的$\theta$：对于θi\\theta_{i}θi​，则有θi=θi−α∂∂θiJ(θ0,θ1,...,θn)\\theta_{i}=\\theta_{i}-\\alpha \\frac{\\partial}{\\partial \\theta_{i}}J(\\theta_{0},\\theta_{1},...,\\theta_{n})θi​=θi​−α∂θi​∂​J(θ0​,θ1​,...,θn​)，更新完毕后转入第一步

三：线性回归典例之波士顿房价预测

（1）波士顿房价数据集

波士顿房价数据集为一个506×14的矩阵，其中最后一个特征是房价

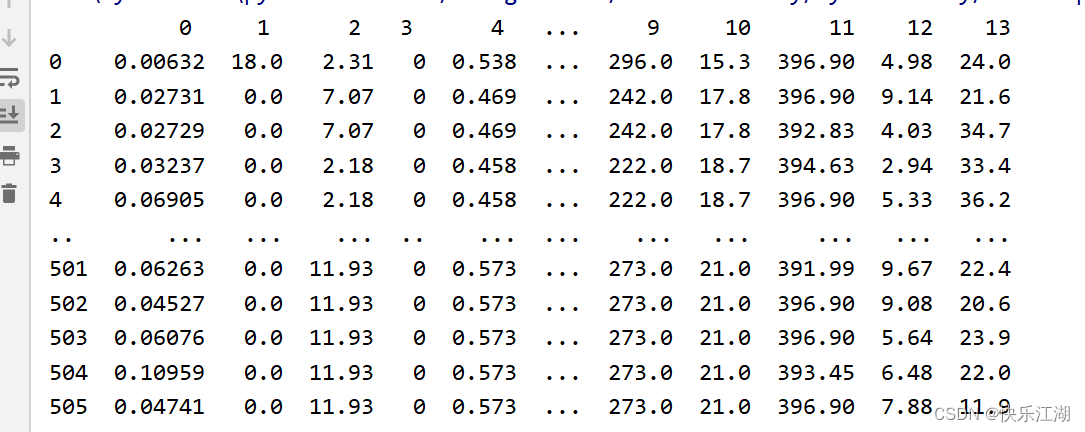
13个维度表示的含义如下

• CRIM 城镇人口犯罪率
• ZN 超过25000平方英尺的住宅用地所占比例
• INDUS 城镇非零售业务地区的比例
• CHAS 查尔斯河虚拟变量(如果土地在河边=1；否则是0)
• NOX 一氧化氮浓度(每1000万份)
• RM 平均每居民房数
• AGE 在1940年之前建成的所有者占用单位的比例
• DIS 与五个波士顿就业中心的加权距离
• RAD 辐射状公路的可达性指数
• TAX 每10,000美元的全额物业税率
• RTRATIO 城镇师生比例
• B 1000(Bk-0.63)^2其中Bk是城镇黑人的比例
• LSTAT 人口中地位较低人群的百分数
• MEDV (目标变量/类别属性)以1000美元计算的自有住房的中位数

（2）手动线性回归

机器学习的一般过程就是建立模型-训练数据，其中模型建立是最困难的过程，而线性回归的模型就是我们上面所提到最小二乘法（以最小二乘法为例）中的公式，我们的目的就是用代码计算

θ=(XTX)−1XTY\\theta = (X^{T}X)^{-1}X^{T}Yθ=(XTX)−1XTY

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
import numpy as np
import pandas as pdnp.set_printoptions(suppress=True)  # 强制使用浮点数显示if os.path.exists('Boston.chache'):raw_data = pd.read_pickle('Boston.chache')else:raw_data = pd.read_csv(r'E:\\Postgraduate\\Course Study\\机器学习-深度学习科研训练\\data\\Boston.csv', sep=' +', engine='python', header=None)raw_data.to_pickle('Boston.chache')raw_data['ONE'] = 1  # 为求截距，增加全1列
data = raw_data.drop(labels=13, inplace=False, axis=1)
price = raw_data[13]  # 真实价格# 计算theta
theta = np.dot(np.dot(np.linalg.inv(np.dot(data.T, data)), data.T), price)  # 1×13向量
print(theta)
print('-'*30)
price_predict = np.dot(data, theta) # 506-13 ×13-1  预测价格
print(price_predict)
print('-'*30)
print(np.mean((price_predict - price) ** 2))  # 均方误差

结果

[ -0.10801136   0.04642046   0.02055863   2.68673382 -17.766611233.80986521   0.00069222  -1.47556685   0.30604948  -0.01233459-0.95274723   0.00931168  -0.52475838  36.45948839] # 最后一个为截距
------------------------------
[30.00384338 25.02556238 30.56759672 28.60703649 27.94352423 25.2562844623.00180827 19.53598843 11.52363685 18.92026211 18.99949651 21.5867956820.90652153 19.55290281 19.28348205 19.29748321 20.52750979 16.9114013516.17801106 18.40613603 12.52385753 17.67103669 15.83288129 13.8062853515.67833832 13.38668561 15.46397655 14.70847428 19.54737285 20.876428211.45511759 18.05923295  8.81105736 14.28275814 13.70675891 23.8146352622.34193708 23.10891142 22.91502612 31.35762569 34.21510225 28.0205641425.20386628 24.60979273 22.94149176 22.09669817 20.42320032 18.036550889.10655377 17.20607751 21.28152535 23.97222285 27.6558508  24.0490180915.3618477  31.15264947 24.85686978 33.10919806 21.77537987 21.0849355517.8725804  18.51110208 23.98742856 22.55408869 23.37308644 30.3614835825.53056512 21.11338564 17.42153786 20.78483633 25.20148859 21.742657724.55744957 24.04295712 25.50499716 23.9669302  22.94545403 23.3569981821.26198266 22.42817373 28.40576968 26.99486086 26.03576297 25.0587348224.78456674 27.79049195 22.16853423 25.89276415 30.67461827 30.8311062327.1190194  27.41266734 28.94122762 29.08105546 27.03977365 28.6245994924.72744978 35.78159518 35.11454587 32.25102801 24.58022019 25.5941347519.79013684 20.31167129 21.43482591 18.53994008 17.18755992 20.7504902622.64829115 19.7720367  20.64965864 26.52586744 20.77323638 20.7154831525.17208881 20.43025591 23.37724626 23.69043261 20.33578364 20.7918087321.91632071 22.47107777 20.55738556 16.36661977 20.56099819 22.4817844614.61706633 15.17876684 18.93868592 14.05573285 20.03527399 19.4101340220.06191566 15.75807673 13.25645238 17.26277735 15.87841883 19.3616395413.81483897 16.44881475 13.57141932  3.98885508 14.59495478 12.14881488.72822362 12.03585343 15.82082058  8.5149902   9.71844139 14.8045137420.83858153 18.30101169 20.12282558 17.28601894 22.36600228 20.1037592313.62125891 33.25982697 29.03017268 25.56752769 32.70827666 36.7746701540.55765844 41.84728168 24.78867379 25.37889238 37.20347455 23.0874874726.40273955 26.65382114 22.5551466  24.29082812 22.97657219 29.0719430826.5219434  30.72209056 25.61669307 29.13740979 31.43571968 32.9223156834.72440464 27.76552111 33.88787321 30.99238036 22.71820008 24.766478135.88497226 33.42476722 32.41199147 34.51509949 30.76109485 30.2893414132.91918714 32.11260771 31.55871004 40.84555721 36.12770079 32.669208134.70469116 30.09345162 30.64393906 29.28719501 37.07148392 42.0319312443.18949844 22.69034796 23.68284712 17.85447214 23.49428992 17.0058771822.39251096 17.06042754 22.73892921 25.21942554 11.11916737 24.5104914826.60334775 28.35518713 24.91525464 29.68652768 33.18419746 23.7745665632.14051958 29.7458199  38.37102453 39.81461867 37.58605755 32.399532535.45665242 31.23411512 24.48449227 33.28837292 38.0481048  37.1632863131.71383523 25.26705571 30.10010745 32.71987156 28.42717057 28.4294067827.29375938 23.74262478 24.12007891 27.40208414 16.3285756  13.3989126120.01638775 19.86184428 21.2883131  24.0798915  24.20633547 25.0421582124.91964007 29.94563374 23.97228316 21.69580887 37.51109239 43.3023904336.48361421 34.98988594 34.81211508 37.16631331 40.98928501 34.4463408935.83397547 28.245743   31.22673593 40.8395575  39.31792393 25.7081790522.30295533 27.20340972 28.51169472 35.47676598 36.10639164 33.7966827435.61085858 34.83993382 30.35192656 35.30980701 38.79756966 34.3312318640.33963075 44.67308339 31.59689086 27.3565923  20.10174154 27.0420667427.2136458  26.91395839 33.43563311 34.40349633 31.8333982  25.8178323724.42982348 28.45764337 27.36266999 19.53928758 29.11309844 31.9105461130.77159449 28.94275871 28.88191022 32.79887232 33.20905456 30.7683179235.56226857 32.70905124 28.64244237 23.58965827 18.54266897 26.8788984323.28133979 25.54580246 25.48120057 20.53909901 17.61572573 18.3758168624.29070277 21.32529039 24.88682244 24.86937282 22.86952447 19.4512379125.11783401 24.66786913 23.68076177 19.34089616 21.17418105 24.2524907321.59260894 19.98446605 23.33888    22.14060692 21.55509929 20.6187290720.16097176 19.28490387 22.1667232  21.24965774 21.42939305 30.3278879622.04734975 27.70647912 28.54794117 16.54501121 14.78359641 25.2738008227.54205117 22.14837562 20.45944095 20.54605423 16.88063827 25.4025350614.32486632 16.59488462 19.63704691 22.71806607 22.20218887 19.2054805722.66616105 18.93192618 18.22846804 20.23150811 37.4944739  14.2819073415.54286248 10.83162324 23.80072902 32.6440736  34.60684042 24.9433133325.9998091   6.126325    0.77779806 25.30713064 17.74061065 20.2327441415.83331301 16.83512587 14.36994825 18.47682833 13.4276828  13.061775123.27918116  8.06022171  6.12842196  5.6186481   6.4519857  14.2076473517.21225183 17.29887265  9.89116643 20.22124193 17.94181175 20.3044578319.29559075 16.33632779  6.55162319 10.89016778 11.88145871 17.8117450718.26126587 12.97948781  7.37816361  8.21115861  8.06626193 19.9829478613.70756369 19.85268454 15.22308298 16.96071981  1.71851807 11.80578387-4.28131071  9.58376737 13.36660811  6.89562363  6.14779852 14.6066179419.6000267  18.12427476 18.52177132 13.1752861  14.62617624  9.9237497616.34590647 14.07519426 14.25756243 13.04234787 18.15955693 18.6955435421.527283   17.03141861 15.96090435 13.36141611 14.52079384  8.819760054.86751102 13.06591313 12.70609699 17.29558059 18.740485   18.0590102911.51474683 11.97400359 17.68344618 18.12695239 17.5183465  17.2274250716.52271631 19.41291095 18.58215236 22.48944791 15.28000133 15.8208933512.68725581 12.8763379  17.18668531 18.51247609 19.04860533 20.1720892719.7740732  22.42940768 20.31911854 17.88616253 14.37478523 16.9477685116.98405762 18.58838397 20.16719441 22.97718032 22.45580726 25.5782462716.39147632 16.1114628  20.534816   11.54272738 19.20496304 21.8627639123.46878866 27.09887315 28.56994302 21.08398783 19.45516196 22.2222591419.65591961 21.32536104 11.85583717  8.22386687  3.66399672 13.7590853815.93118545 20.62662054 20.61249414 16.88541964 14.01320787 19.1085414421.29805174 18.45498841 20.46870847 23.53334055 22.37571892 27.627426126.12796681 22.34421229]
------------------------------
21.8948311817292

（3）scikit-learn实现

具体训练时还要注意以下几点

• 如果没有测试数据，那么不能将全部数据都用作训练，需要拆分出一部分数据。使用scikit-learn中的train_test_split函数即可
• 训练完成后需要画图进行分析
• 如果数据过大或过小往往要取对数
• 对于某些数据可能要进行one-hot编码（后面说到）

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
import numpy as np
import pandas as pd
from sklearn.linear_model import  LinearRegression
from sklearn.metrics import mean_squared_error  # 均方误差
from sklearn.metrics import mean_absolute_error  # 平方绝对误差
from sklearn.model_selection import train_test_split  # 训练测试分割np.set_printoptions(suppress=True)  # 强制使用浮点数显示if os.path.exists('Boston.chache'):raw_data = pd.read_pickle('Boston.chache')else:raw_data = pd.read_csv(r'E:\\Postgraduate\\Course Study\\机器学习-深度学习科研训练\\data\\Boston.csv', sep=' +', engine='python', header=None)raw_data.to_pickle('Boston.chache')data = raw_data[np.arange(13)]
price = raw_data[13]  # 真实价格# 拆分数据，其中 80%训练，20%测试
data_train, data_test, price_train, price_test = train_test_split(data, price, test_size=0.2, random_state=520) # random_state仅为了固定随机种子# 线性回归训练
model = LinearRegression(fit_intercept=True)  # fit_intercept = True表示也训练截距
model.fit(data_train, price_train)  # 训练
theta = model.coef_  # 系数
intercept = model.coef_  # 截距
price_train_predict = model.predict(data_train)  # 结果预测
MSE_train = mean_squared_error(price_train, price_train_predict)  # 均方误差
MAE_train = mean_absolute_error(price_train, price_train_predict)  # 平方绝对误差# 测试数据
price_test_predict = model.predict(data_test)
MSE_test = mean_squared_error(price_test, price_test_predict)  # 均方误差
MAE_test = mean_absolute_error(price_test, price_test_predict)  # 平方绝对误差# 模型分析
# 训练集
err_train = price_train_predict - price_train
plt.hist(err_train, bins=20, edgecolor='k')
plt.title('Train set error histogram', size=16)
plt.grid(True, color='gray', linestyle=':')# 测试集
err_test = price_test_predict - price_test
plt.figure()
plt.hist(err_test, bins=20, edgecolor='k')
plt.title('Test set error histogram', size=16)
plt.grid(True, color='gray', linestyle=':')
plt.show()

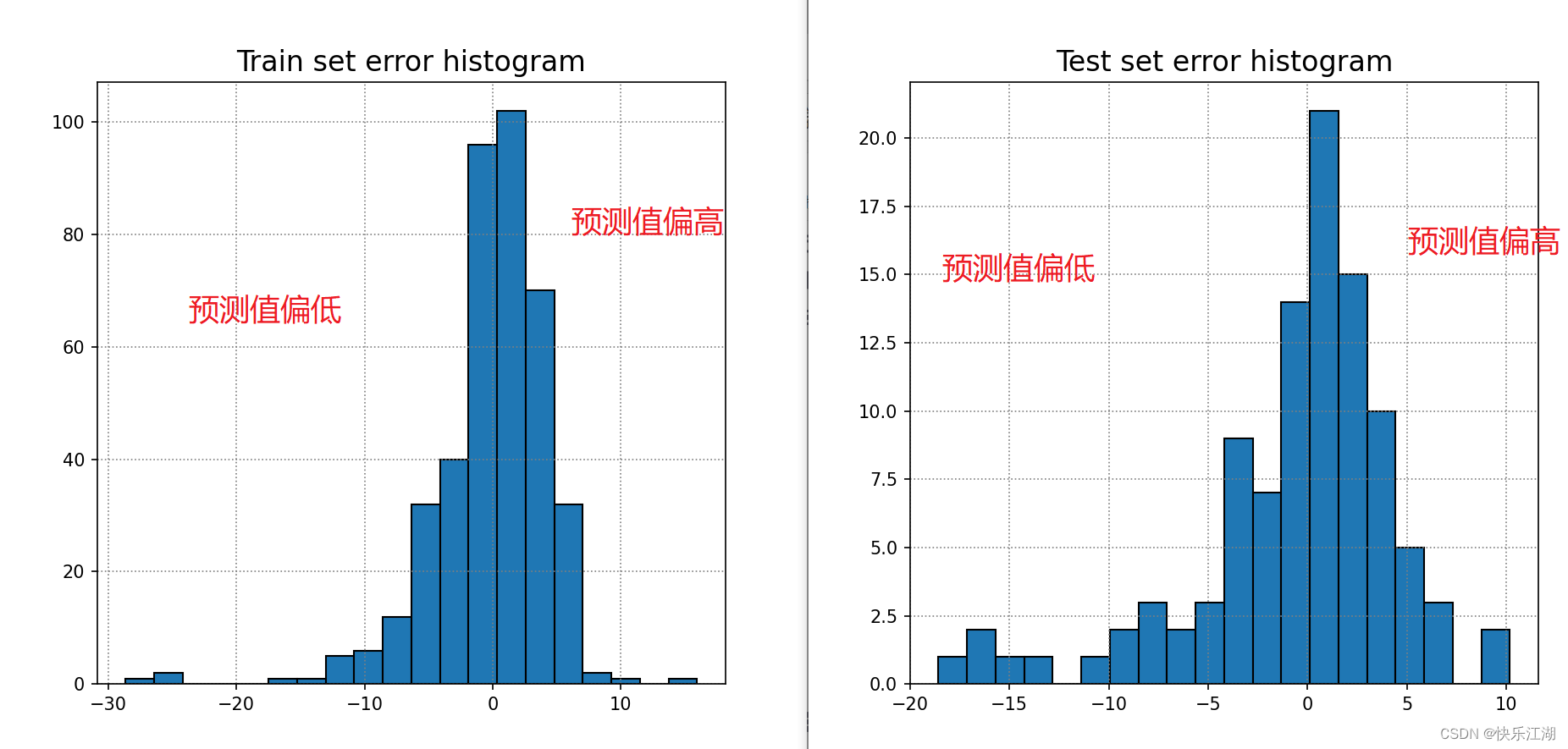
（4）one-hot编码

A：什么是one-hot编码

专业的术语就再不说了，这里我们以“hello world”为例，进行one-hot编码，步骤如下

• 确定编码对象：hello world
• 确定分类变量：h e l l o 空格 w o r l d，共27种类别（26个小写字母+空格）
• 转换问题：以上问题等价于有11个样本，每个样本有27个特征，将其转化为二进制向量表示

需要注意特征排列的顺序不同，对应的二进制向量亦不同，所以要事先约定特征排列的顺序

• 27种特征首先进行整数编码：a-0，b-1,…,z-25，空格-26
• 27种特征按照整数编码大小从前往后排列

得到one-hot编码如下

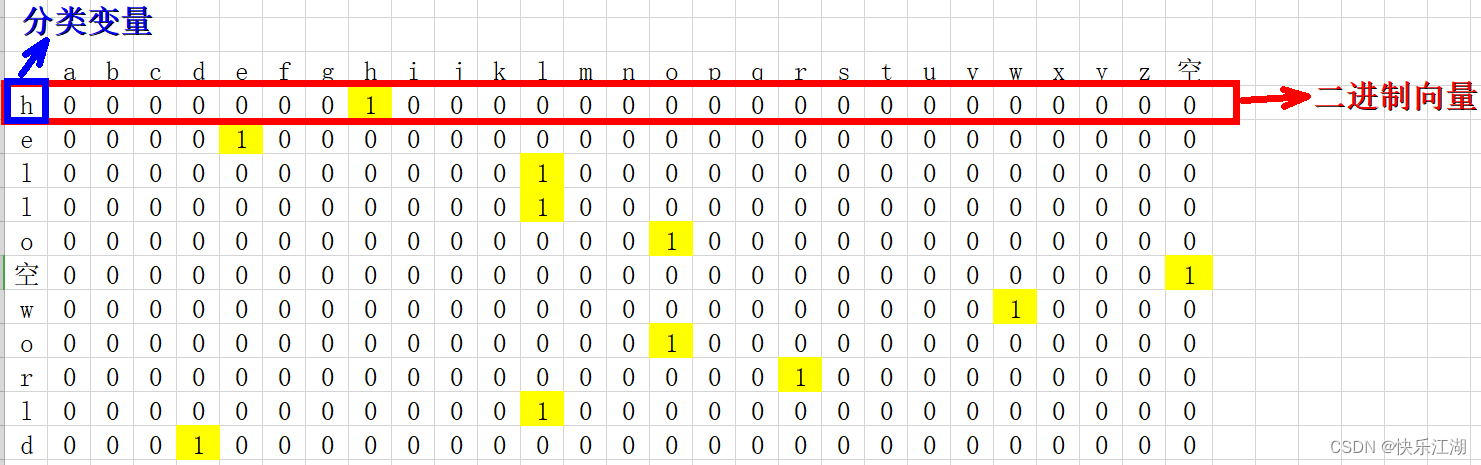
B：什么情况下会使用one-hot编码

• 对于定类类型的数据，建议使用one-hot encodin：定类类型就是纯分类，不排序，没有逻辑关系：比如性别分男和女，男女不存在任何逻辑关系，我们不能说男就比女好，或者相反。再者，中国各省市分类也可以用独热编码，同样各省不存在逻辑关系，这时候使用one-hot encoding会合适些。但注意，一般会舍去一个变量，比如男的对立面肯定是女，那么女就是重复信息，所以保留其中一个变量即可
• 对于定序类型的数据，建议使用label encoding。定序类型也是分类，但有排序逻辑关系，等级上高于定类：比如，学历分小学，初中，高中，本科，研究生，各个类别之间存在一定的逻辑，显然研究生学历是最高的，小学最低。这时候使用Label encoding会显得更合适，因为自定义的数字顺序可以不破坏原有逻辑，并与这个逻辑相对应。
• 对数值大小敏感的模型必须使用one-hot encoding或者Dummy：典型的例子就是LR和SVM。二者的损失函数对数值大小是敏感的，并且变量间的数值大小是有比较意义的。而Label encoding的数字编码没有数值大小的含义，只是一种排序，因此对于这些模型都使用one-hot encoding。
• 对数值大小不敏感的模型（如树模型）不建议使用one-hot encoding：一般这类模型为树模型。如果分类类别特别多，那么one-hot encoding会分裂出很多特征变量。这时候，如果我们限制了树模型的深度而不能向下分裂的话，一些特征变量可能就因为模型无法继续分裂而被舍弃损失掉了。因此，此种情况下可以考虑使用Label encoding

四：逻辑回归（对数几率回归）

（1）对数几率函数

对于二分类任务来说，其输出标记为y∈{0,1}y\\in\\{0,1\\}y∈{0,1}，而前文所说线性回归模型产生的预测值z=wTx+Bz=w^{T}x+Bz=wTx+B为实值，产生了矛盾。因此我们需要将实值$z$转化为$0/1$值，最理想的便是“单位阶跃函数”

y={0,z<00.5,z=01,z>0y=\\left\\{\\begin{array}{cc} 0, & z<0 \\\\ 0.5, & z=0 \\\\ 1, & z>0 \\end{array}\\right. y=⎩⎨⎧​0,0.5,1,​z<0z=0z>0​

但问题是单位阶跃函数并不连续，其关于$x$的导数为0，所以难以使用梯度下降法进行优化更新，因此需要一个可以在$(0,1)$之间平滑过度的函数。而对数几率函数就是一个这样比较合适的函数

y=11+e−zy=\\frac{1}{1+e^{-z}} y=1+e−z1​

对数几率函数是一种“Sigmoid”函数，它将$z$转化为一个接近0或1的$y$值，并且其输出值在$z=0$处很陡。将对数几率函数代入广义线性模型y=g−1(wTx+b)y=g^{-1}(w^{T}x+b)y=g−1(wTx+b)中，可得

y=11+e−(wTx+b)y=\\frac{1}{1+e^{-(w^{T}x+b)}}y=1+e−(wTx+b)1​

可变化为

ln⁡y1−y=wTx+b\\ln \\frac{y}{1-y}=w^{T}x+b ln1−yy​=wTx+b
若将$y$视为样本$x$作为正例的可能性，则$1-y$就是其为反例的可能性，如下两者之比称之为几率

y1−y\\frac{y}{1-y} 1−yy​

几率反映了$x$作为正例的相对可能性，对几率取对数则得到对数几率

ln⁡y1−y\\ln \\frac{y}{1-y}ln1−yy​

（2）利用极大似然估计推导损失函数

• 此部分借助周志华机器学习

（3）实例：二分类问题

导入必要的库

import numpy as np
import matplotlib.pyplot as pltnp.random.seed(1234)

数据制作与处理

num=100
# 负例样本
x_1 = np.random.normal(3,1,size=num)
x_2 = np.random.normal(6,1,size=num)
y = np.zeros(num)
c_0 = np.array([x_1, x_2, y])
c_0 = c_0.T# 正例样本
x_1 = np.random.normal(6,1,size=num)
x_2 = np.random.normal(3,1,size=num)
y = np.ones(num)
c_1 = np.array([x_1, x_2, y])
c_1 = c_1.T# 可视化
plt.scatter(c_0[:,0], c_0[:,1], marker='.')
plt.scatter(c_1[:,0], c_1[:,1], marker='+')
plt.xlabel('x_1')
plt.xlabel('x_2')
plt.show()# 制作数据集，拆分为训练集测试集
all_data = np.concatenate((c_0,c_1))
np.random.shuffle(all_data)
train_data_X = all_data[:160,:2]
train_data_y = all_data[:160,-1]
test_data_X = all_data[160:,:2]
test_data_y = all_data[160:,-1]
print("所有数据：",np.shape(all_data))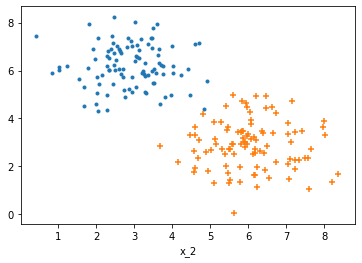

​

构建logistic函数

def logistic(z):return 1./(1.+ np.exp(-z))

定义交叉熵损失函数

def loss_func(y,y_hat):return -np.mean(y*np.log(y_hat) + (1-y)*np.log(1-y_hat))

训练

#  定义学习率和训练次数
lr = 0.1
epochs = 1000
w=np.random.rand(2,1)w_list = []loss_list = []
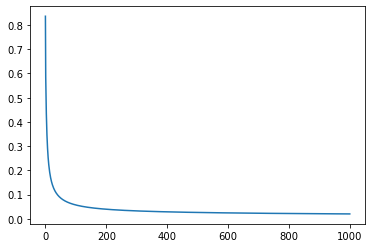
for i in range(epochs):y_hat = logistic(np.dot(w.T, train_data_X.T)).reshape(-1)         loss = loss_func(train_data_y,y_hat)grad_w = -np.mean(train_data_X*((train_data_y-y_hat).reshape(-1,1)),axis=0)w = w-(lr*grad_w).reshape(2,1)w_list.append(w)loss_list.append(loss)if i%100 == 0:print("i:{},loss:{}".format(i,loss))if loss<0.0001:breakplt.plot(loss_list)
plt.show()

i:0,loss:0.8362037267203654
i:100,loss:0.0569645296423402
i:200,loss:0.0394426808919077
i:300,loss:0.03252589615836855
i:400,loss:0.028653376288426135
i:500,loss:0.026114494074833856
i:600,loss:0.024291498453630045
i:700,loss:0.02290266331908917
i:800,loss:0.02179961447586222
i:900,loss:0.020896107954759952

x = np.arange(1,9)
y = -(w[0]*x)/w[1]
plt.plot(x,y,'r')
plt.scatter(c_0[:,0], c_0[:,1], marker='.')
plt.scatter(c_1[:,0], c_1[:,1], marker='+')
plt.xlabel('x_1')
plt.xlabel('x_2')
plt.show()

五：线性判别分析（LDA）

（1）概述

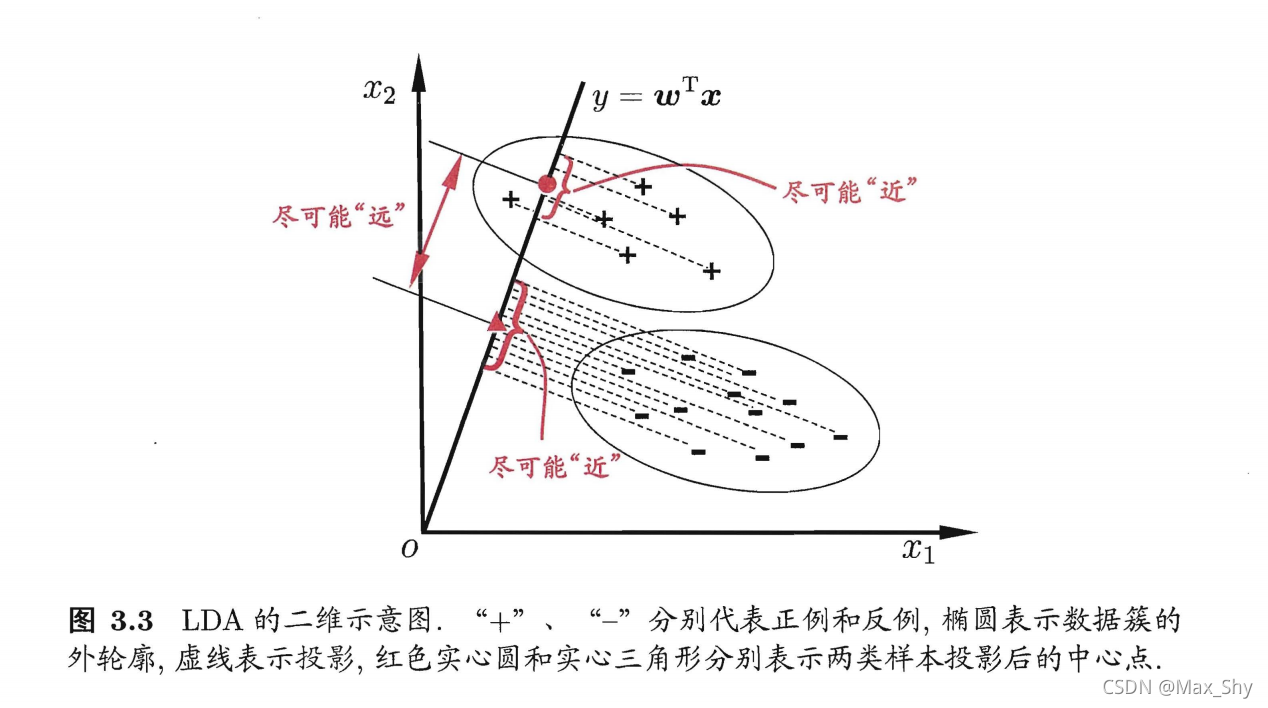
线性判别分析（Linear Discriminant Analysis，LDA）：是一种经典的统计学习方法，它的主要目的是通过将高维数据投影到一个低维子空间，来实现数据分类和降维的目的。LDA的应用非常广泛，尤其在有监督学习中的分类问题上表现优秀。LDA的基本思想是：给定训练样本集，设法将样例投影到一条直线上。使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远；在对新样本进行分类时，将其投影到该直线上，再根据投影点的位置来确定新样本的类别

（2）原理

• 此部分借助周志华机器学习

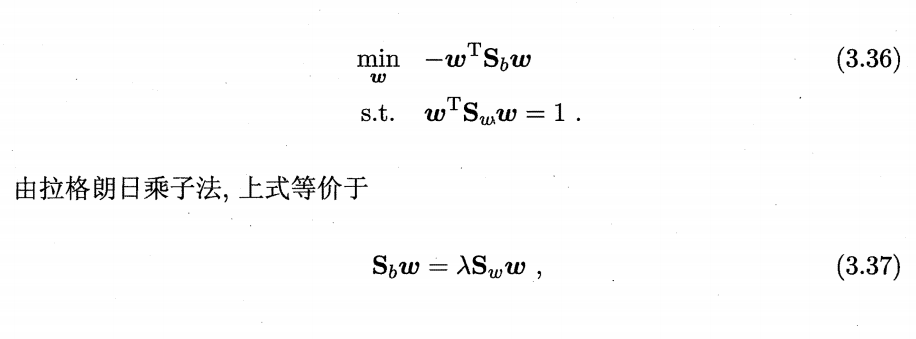
（3）实例

导入必要的库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.datasets import make_classification

数据制作与处理

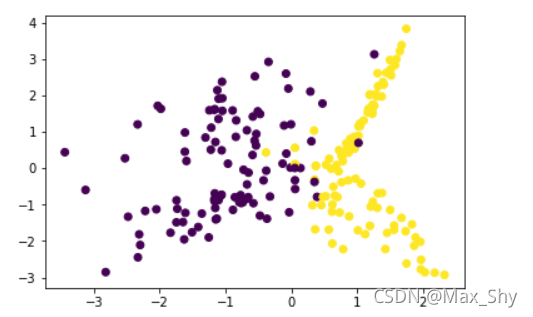
x, y = make_classification(n_samples=200, n_features=2, n_redundant=0, n_classes=2, n_informative=2,n_clusters_per_class=2,class_sep =1, random_state =0)
fig = plt.figure()
plt.scatter(x[:, 0], x[:, 1], c=y)

#设置分类平滑度
h = .01
#设置X和Y的边界值
x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1#使用meshgrid函数返回X和Y两个坐标向量矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max,h), np.arange(y_min, y_max,h))
Z = lda.predict(np.c_[xx.ravel(), yy.ravel()])

LDA分类

#使用LDA进行降维
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis 
from sklearn.linear_model import LogisticRegression
lda = LinearDiscriminantAnalysis(n_components=1)x_train_lda = lda.fit_transform(x_train, y_train)  # LDA是有监督方法，需要用到标签
x_test_lda = lda.fit_transform(x_test, y_test)   # 预测时候特征向量正负问题，乘-1反转镜像

绘制分类图像

#设置colormap颜色
cm_bright = ListedColormap(['#D9E021', '#0D8ECF'])
#绘制数据点
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train, cmap=cm_bright)
plt.title('Linear Discriminant Analysis Classifiers')
plt.axis('tight')
plt.show()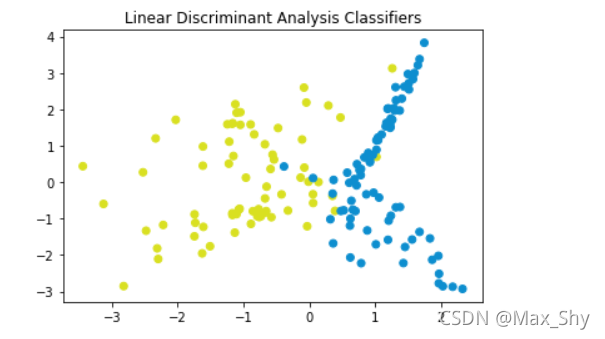

plt.title('Linear Discriminant Analysis Classifiers')
plt.scatter(x_test[:, 0], x_test[:, 1], c=y_test, cmap=cm_bright)
plt.show()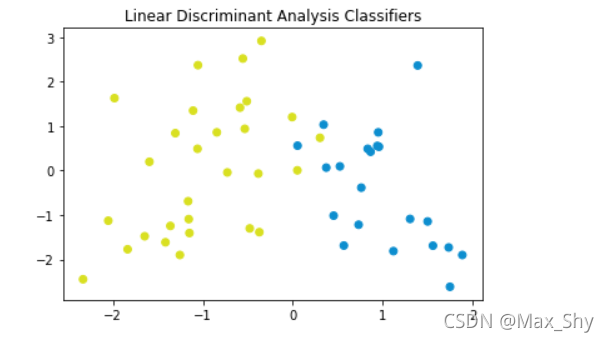

六：总结

线性回归（Linear Regression）是一种广泛应用于机器学习中的模型，其主要用途是对输入变量和输出变量之间的关系进行建模，并利用该模型进行预测线性回归模型假设输入变量（自变量）和输出变量（因变量）之间存在线性关系，可以用一个线性函数来描述它们之间的关系。简单线性回归模型是指只有一个输入变量和一个输出变量的情况，其模型可以表示为：

$$y=b0+b1\ast x+\epsilon$$

在实际应用中，通常使用最小二乘法来估计模型的参数，该方法的目标是最小化实际输出变量和预测输出变量之间的差距，即最小化误差平方和（SSE）。具体来说，最小二乘法会寻找一组最优参数b0和b1，使得SSE最小。

线性回归模型的优点是简单易懂，计算速度快，可解释性强。同时，它也有一些局限性，如对于非线性关系的建模效果不佳，容易受到异常值和噪声的影响等。因此，在实际应用中需要根据具体问题选择适合的模型和算法。

总之，线性回归是一种基础且常用的机器学习模型，其思想简单，适用范围广泛，在各种应用场景中都有着重要的作用