我们在训练模型时学习率的设置非常重要。

• 学习率的大小很重要。如果它太大，优化就会发散，如果它太小，训练时间太长，否则我们最终会得到次优的结果。
• 其次，衰变率同样重要。如果学习率仍然很大，我们可能会简单地在最小值附近反弹，从而无法达到最优

我们可以通过学习率时间表（Learning Rate Scheduling）有效地管理准确性

一、基于FashionMNIST任务的学习率时间表实践准备

构建简单网络

def net_fn():model = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.ReLU(),nn.MaxPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), nn.ReLU(),nn.MaxPool2d(kernel_size=2, stride=2),nn.Flatten(),nn.Linear(16 * 5 * 5, 120), nn.ReLU(),nn.Linear(120, 84), nn.ReLU(),nn.Linear(84, 10))return model

模型结构如下（左-netron）

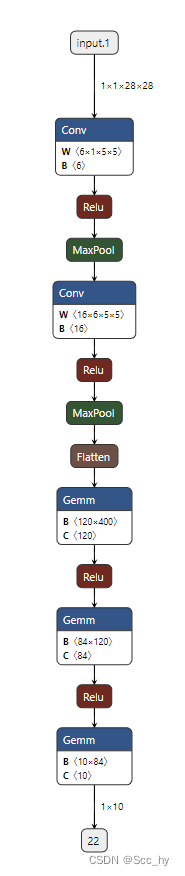
简单的训练框架
全部脚本可以查看笔者的github: LearningRateScheduling.ipynb

def train(model, train_iter, test_iter, config, scheduler=None):device = config.deviceloss = config.lossopt = config.optnum_epochs = config.num_epochsmodel.to(device)animator = Animator(xlabel='epoch', xlim=[0, num_epochs],legend=['train loss', 'train acc', 'test acc'])ep_total_steps = len(train_iter)for ep in range(num_epochs):tq_bar = tqdm(enumerate(train_iter))tq_bar.set_description(f'[ Epoch {ep+1}/{num_epochs} ]')# train_loss, train_acc, num_examplesmetric = Accumulator(3)for idx, (X, y) in tq_bar:final_flag = (ep_total_steps == idx + 1) & (num_epochs == ep + 1)model.train()opt.zero_grad()X, y = X.to(device), y.to(device)y_hat = model(X)l = loss(y_hat, y)l.backward()opt.step()with torch.no_grad():metric.add(l * X.shape[0], accuracy(y_hat, y), X.shape[0])train_loss = metric[0] / metric[2]train_acc = metric[1] / metric[2]tq_bar.set_postfix({"loss" : f"{train_loss:.3f}","acc" : f"{train_acc:.3f}",})if (idx + 1) % 50 == 0:animator.add(ep + idx / len(train_iter), (train_loss, train_acc, None), clear_flag=not final_flag)test_acc = evaluate_accuracy_gpu(model, test_iter)animator.add(ep+1, (None, None, test_acc), clear_flag=not final_flag)if scheduler:if scheduler.__module__ == lr_scheduler.__name__:# 使用 PyTorch In-Built schedulerscheduler.step()else:# 使用自定义 schedulerfor param_group in opt.param_groups:param_group['lr'] = scheduler(ep) print(f'train loss {train_loss:.3f}, train acc {train_acc:.3f}, 'f'test acc {test_acc:.3f}')plt.show()

二、基于FashionMNIST任务的学习率时间表实践

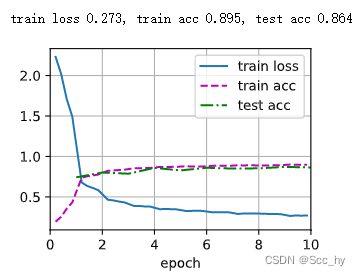
2.1 无learning rate Scheduler 训练

def test(train_iter, test_iter, scheduler=None):net = net_fn()cfg = Namespace(device=try_gpu(),loss=nn.CrossEntropyLoss(),lr=0.3, num_epochs=10,opt=torch.optim.SGD(net.parameters(), lr=0.3))train(net, train_iter, test_iter, cfg, scheduler)batch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size=batch_size)
test(train_iter, test_iter)

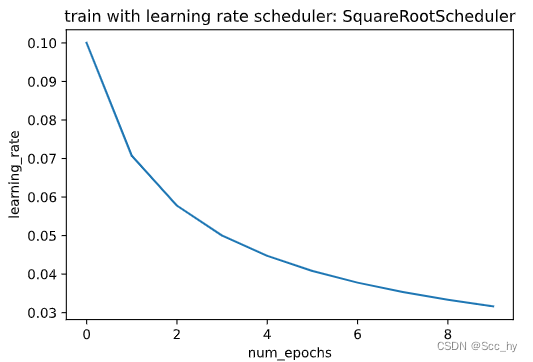
2.2 Square Root Scheduler训练

更新方式为
η=η∗num_update+1\\eta =\\eta *\\sqrt{num\\_update + 1}η=η∗num_update+1​
本次试验是每一个epoch更新一次

def get_lr(scheduler):lr = scheduler.get_last_lr()[0]scheduler.optimizer.step()scheduler.step()return lrdef plot_scheduler(scheduler, num_epochs=10):s = scheduler.__class__.__name__if scheduler.__module__ == lr_scheduler.__name__:print('pytorch build lr_scheduler')plot_y = [get_lr(scheduler) for _ in range(num_epochs)]else:plot_y = [scheduler(t) for t in range(num_epochs)]plt.title(f'train with learning rate scheduler: {s}')plt.plot(torch.arange(num_epochs), plot_y)plt.xlabel('num_epochs')plt.ylabel('learning_rate')plt.show()class SquareRootScheduler:"""使用均方根scheduler每一个epoch更新一次"""def __init__(self, lr=0.1):self.lr = lrdef __call__(self, num_update):return self.lr * pow(num_update + 1.0, -0.5)scheduler = SquareRootScheduler(lr=0.1)
plot_scheduler(scheduler)

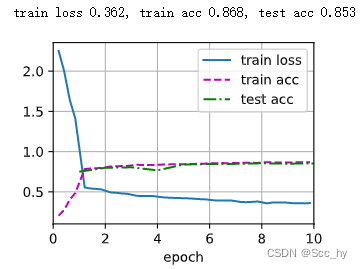
训练

test(train_iter, test_iter, scheduler)

从下图中可以看出：曲线比以前更平滑了。其次，过度拟合较少。

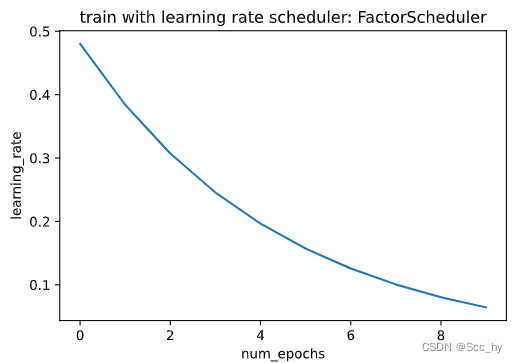
2.3 FactorScheduler训练

学习率更新方式: ηt+1←max(ηmin,ηt⋅α)\\eta_{t+1} \\leftarrow \\mathop{\\mathrm{max}}(\\eta_{\\mathrm{min}}, \\eta_t \\cdot \\alpha)ηt+1​←max(ηmin​,ηt​⋅α)

class FactorScheduler:def __init__(self, factor=1, stop_factor_lr=1e-7, base_lr=0.1):self.factor = factorself.stop_factor_lr = stop_factor_lrself.base_lr = base_lrdef __call__(self, num_update):self.base_lr = max(self.stop_factor_lr, self.base_lr * self.factor)return self.base_lrscheduler = FactorScheduler(factor=0.8, stop_factor_lr=1e-2, base_lr=0.6)
plot_scheduler(scheduler)

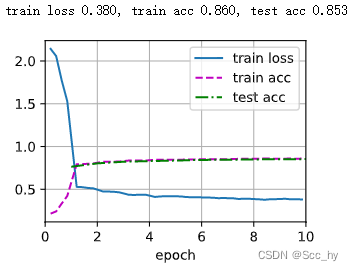
训练

test(train_iter, test_iter, scheduler)

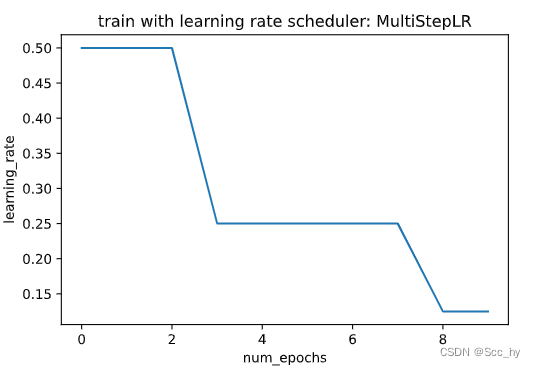
2.4 Multi Factor Scheduler训练

保持学习率分段恒定，并每隔一段时间将其降低一个给定的量。也就是说，给定一组何时降低速率的时间比如$ (s = {3, 8} )$
decrease(ηt+1←ηt⋅α)t∈sdecrease (\\eta_{t+1} \\leftarrow \\eta_t \\cdot \\alpha) \\ \\ t \\in sdecrease(ηt+1​←ηt​⋅α)  t∈s

net = net_fn()
trainer = torch.optim.SGD(net.parameters(), lr=0.5)
scheduler = lr_scheduler.MultiStepLR(trainer, milestones=[3, 8], gamma=0.5)plot_scheduler(scheduler)

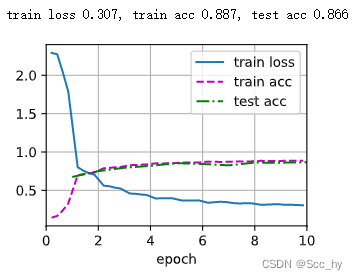
训练

test(train_iter, test_iter, scheduler)

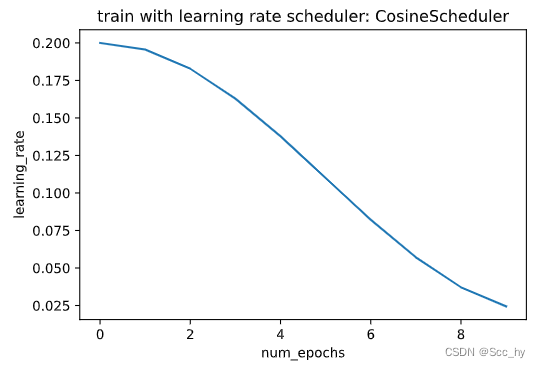
2.5 Cosine Scheduler训练

Loshchilov和Hutter提出了一个相当令人困惑的启发式方法。它依赖于这样一种观察，即我们可能不想在一开始就大幅降低学习率，此外，我们可能希望在最后使用非常小的学习率来“完善”解决方案。这导致了一个类似余弦的时间表，具有以下函数形式，用于范围内的学习率$t\in [0,T]$

ηt=ηT+η0−ηT2(1+cos⁡(πtT))\\eta_t = \\eta_T + \\frac{\\eta_0 - \\eta_T}{2} \\left(1 + \\cos(\\frac{\\pi t}{T})\\right)ηt​=ηT​+2η0​−ηT​​(1+cos(Tπt​))

注：

• ηT\\eta_TηT​: 为最终的学习率
• η0\\eta_0η0​: 为最开始的学习率

class CosineScheduler:def __init__(self, max_update, base_lr=0.01, final_lr=0,warmup_steps=0, warmup_begin_lr=0):self.base_lr_orig = base_lrself.max_update = max_updateself.final_lr = final_lrself.warmup_steps = warmup_stepsself.warmup_begin_lr = warmup_begin_lrself.max_steps = self.max_update - self.warmup_stepsdef get_warmup_lr(self, step):increase = (self.base_lr_orig - self.warmup_begin_lr) \\* float(step) / float(self.warmup_steps)return self.warmup_begin_lr + increasedef __call__(self, step):if step < self.warmup_steps:return self.get_warmup_lr(step)if step <= self.max_update:self.base_lr = self.final_lr + (self.base_lr_orig - self.final_lr) * (1 + math.cos(math.pi * (step - self.warmup_steps) / self.max_steps)) / 2return self.base_lrscheduler = CosineScheduler(max_update=10, base_lr=0.2, final_lr=0.02)
plot_scheduler(scheduler)

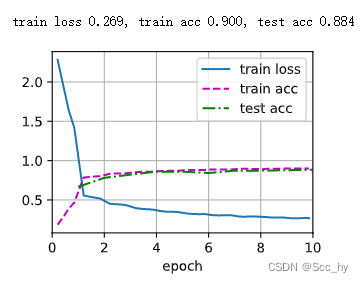
训练

test(train_iter, test_iter, scheduler)

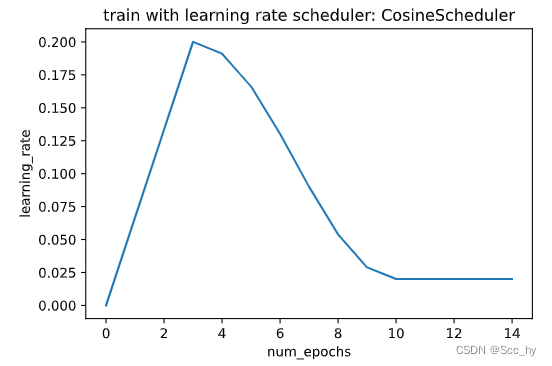
2.6 Warmup

在某些情况下，初始化参数不足以保证良好的解决方案。对于一些先进的网络设计来说，这尤其是一个问题（Transformer的训练常用该方法），可能会导致不稳定的优化问题。
我们可以通过选择一个足够小的学习率来解决这个问题，以防止一开始就出现分歧。不幸的是，这意味着进展缓慢。相反，学习率高最初会导致差异。

对于这种困境，一个相当简单的解决方案是使用一个预热期，在此期间学习速率增加到其初始最大值，并冷却速率直到优化过程结束。为了简单起见，通常使用线性增加来实现这一目的。

scheduler = CosineScheduler(max_update=10, warmup_steps=3, base_lr=0.2, final_lr=0.02)
plot_scheduler(scheduler, 15)

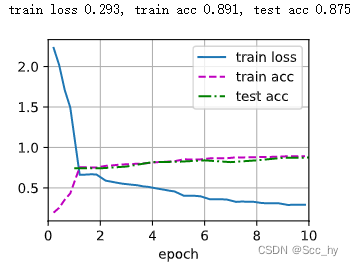
训练

test(train_iter, test_iter, scheduler)

小结

从上述的5个策略上来看，一般情况我们用 Cosine Scheduler 或者线性衰减就能得到较好的结果。不过对于较大的模型，需要用warmup 并且需要特意去设计，比如NoamOpt等。