大数除法【分治、算法推导】

算法推导

假设当前我们有一个1234 ÷ 11

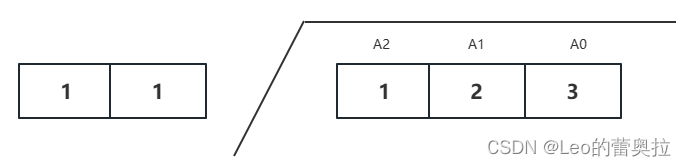
首先执行第一位1 ÷ 11 = 0…1

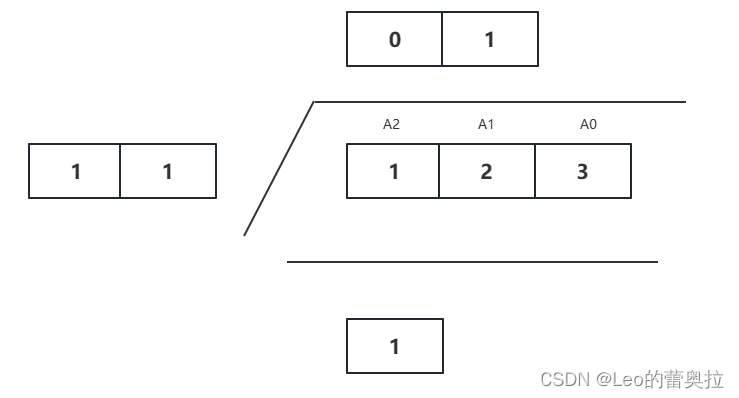
然后执行下一步 1 * 10 + 2 = 12，用新的12 ÷ 11 = 1…1

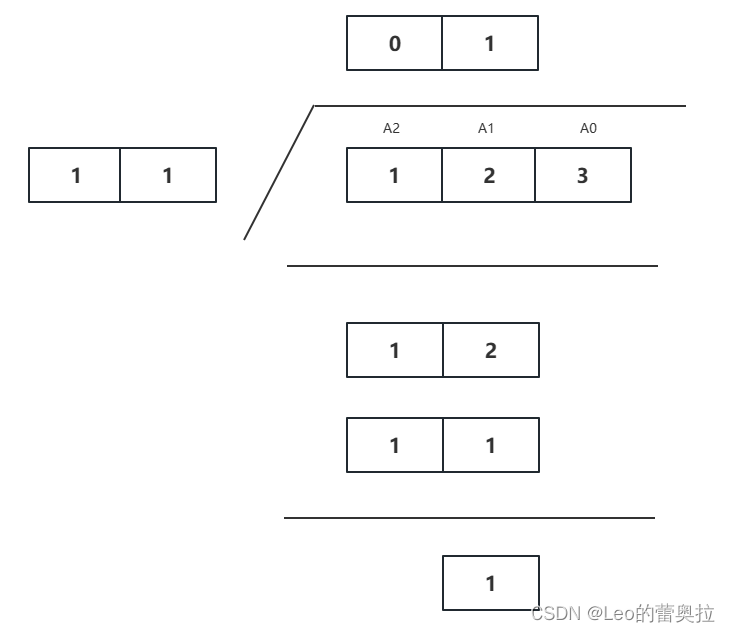
继续执行 1 * 10 + 3 = 13 ，用13 ÷ 11 = 1 …2

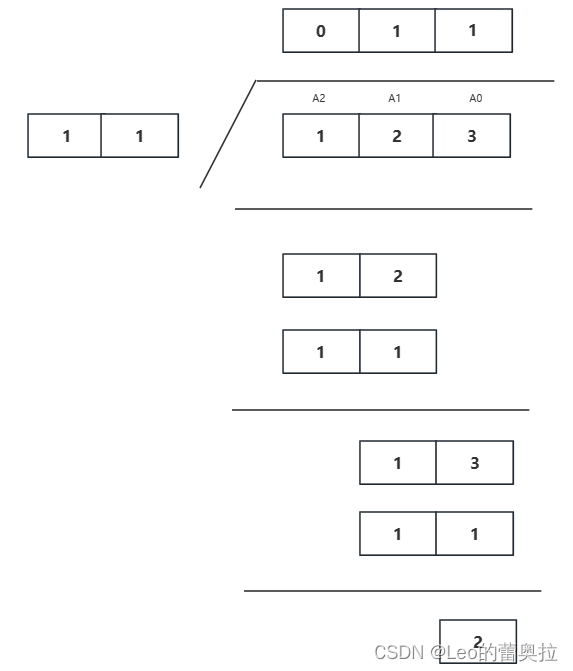
所以最后的结果就是 123 ÷ 11 = 11…2

抽象一下

其实我们这里就是直接进行相除运算的，首先对第一位1进行运算，直接 ÷ 11 后放入答案

余数就是 % 11；然后下一个数 需要在余数的基础上 ，进行相除运算

可以得到一下核心代码

r = 0;不断遍历大数
r = r * 10 + A[i]C.push_back(r / b)r %= b;

代码模板

#include<iostream>
#include<vector>
#include<algorithm>using namespace std;vector<int> div(vector<int> &A , int b , int &r){r = 0 ;vector<int> C;for(int i = A.size() -1 ; i >= 0 ; i --){r = r * 10 + A[i];C.push_back(r / b);r %= b;}reverse(C.begin() , C.end());while(C.size() > 1 && C.back() == 0) C.pop_back();return C;}int main(){string a;int b ;cin >> a >> b;vector<int> A;for(int i = a.size() - 1 ; i >= 0 ; i --) A.push_back(a[i] - '0');int r = 0;vector<int> C = div(A , b , r);for(int i = C.size() - 1 ; i >= 0 ; i --) cout << C[i];cout << endl << r ;return 0;
}

输入

虽然这里是从最高位开始相除的，但是我们还是延续之前的高精读算法，从最后开始存

因为大部分的高精读运算是将其相互混合在一起的，所以为了方便这里直接整合在一起了

问题一：为什么要reverse一下？

因为这里虽然我们是直接从倒序读取A，然后结果就是正的

但是

• 为方便处理，最后还是倒序输出
• 方便处理前置0 （同样是方便前导0的统一处理）