题目描述

输入一个整数N，判断其是否可以表示成一个正整数阶乘的形式或者几个不同正整数的阶乘之和。

输入要求

输入一个整数N。

输出要求

对应该整数N，若可以表示，输出YES，否则输出NO

输入样例

4
-1
0
6
^Z

输出样例

NO
NO
NO
YES

提示

单个整数阶乘的最大值到12!，即479001600。

来源

NBU OJ

思路:
假设a<b<c;如果n=a!+b!+c!,则n=a!(1+ (a+1)(a+2)* *(b)+ (a+1)(a+2)* *(b)*(b+1) *(c)）;（相当于把公因素a！提取出来到红色括号外）
则n可以整除a!。

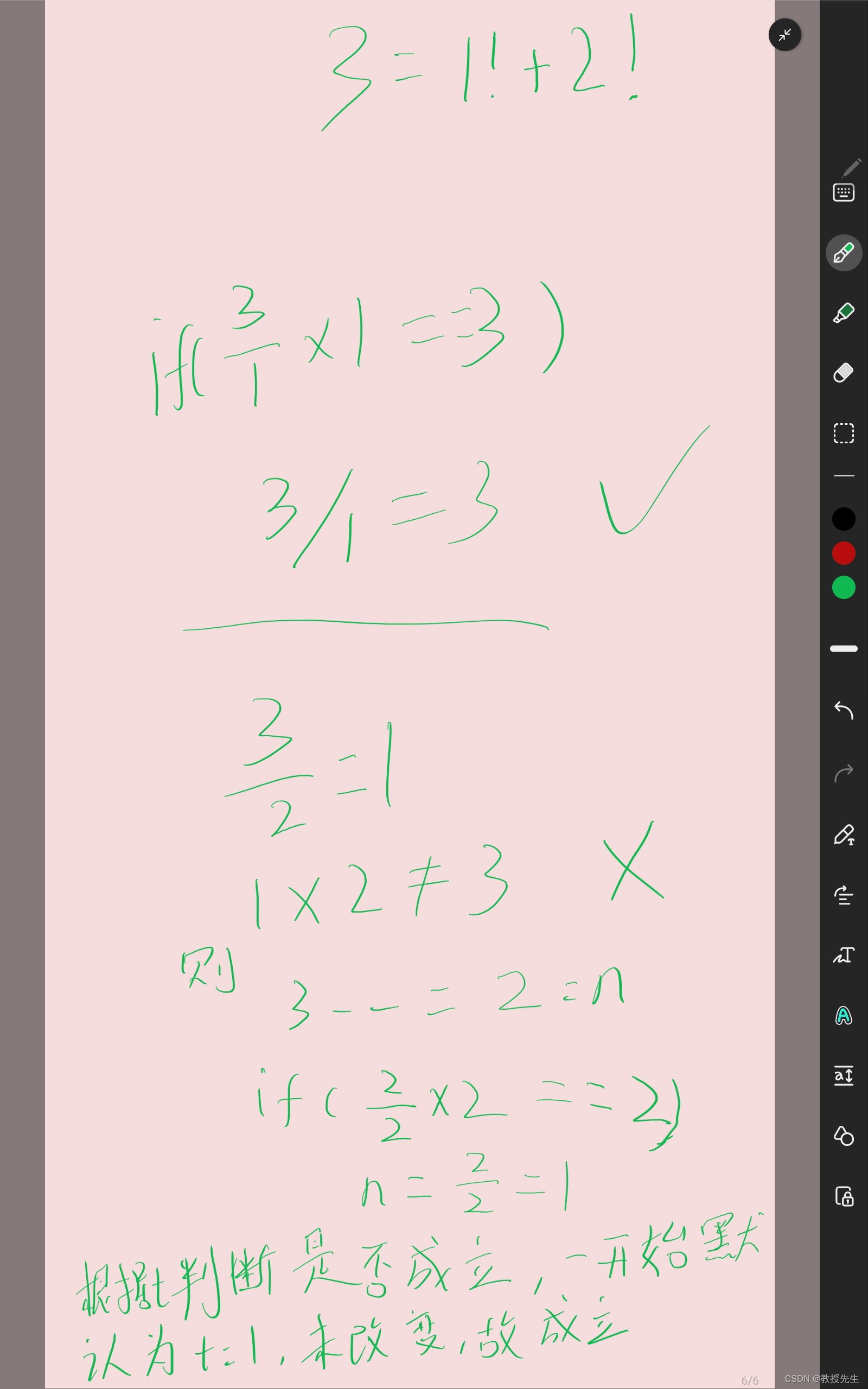
可以看出，如果n是阶乘之和，则从i=1开始递增，如果n可以整除i，则n不断除以i，直到遇到n不能整除i，则(n-1)一定可以整除i。
 

举例说明，比如说i递增到了a，n除于a！，若n=a!+b!+c!条件成立，则一定可以整除a。

然后再减去1（橙色那个），此时i又递增了1，变成了a+1，若n=a!+b!+c!条件成立，则一定可以整除a+1，这是他们的公因数。

#include <stdio.h>int main() {int n, t;while (scanf("%d", &n) != EOF) //多组输入 {if (n > 0) {int i = 1;//i从1开始递增 t = 1;while (n > 1)//如果n<=0,则表示除干净了，可以跳出循环，判断t，t是1则n=a!+b!+c!条件成立，t是0则反之 {if (((n / i)*i) == n)//如果除了i再乘上i等于原来的数，说明能被整除，如果不等于，说明不能被整除，就可以进行n-1判断是否能被i整除， {n /= i;} else {n--;if (((n / i)*i) == n)//如果成立，肯定能被整除 {n /= i;} else//不成立,则不能被整除，改变t为0，作为标记，结果判断输出NO {t = 0;break;}}i++;}if (t)printf("YES\\n");elseprintf("NO\\n");} elseprintf("NO\\n");}return 0;
}

 本文代码及其方法是在借鉴这个博客

1106 是否阶乘之和？_Mlers_9的博客-CSDN博客

尊重作者版权，故此引用。