LeetCode练习九:树(上)——树的定义及遍历、二叉搜索树

文章目录
-
- 一、 树
-
- 1.1 树的定义
- 1.2 二叉树
-
- 1.2.1 完全二叉树
- 1.2.1 满二叉树
- 1.2.3 二叉堆
- 1.2.4 二叉搜索树
- 1.2.5 平衡二叉搜索树
- 1.3 二叉树的实现
-
- 1.3.1 嵌套列表法(顺序存储)
- 1.3.2 节点链接法(链式存储)
- 1.4 树的应用:表达式解析
- 二、 树的遍历Tree Traversals
-
- 2.1 前序遍历
-
- 2.1.1 前序遍历的递归实现
- 2.1.2 前序遍历的显式栈实现
- 2.2 中序遍历
-
- 2.2.1 中序遍历的递归实现
- 2.2.1 中序遍历的显式栈实现
- 2.3 后序遍历
-
- 2.3.1 后序遍历的递归实现
- 2.3.2 后序遍历的显式栈实现
- 2.4 层序遍历
- 2.5 二叉树的遍历题目
-
- 2.5.1 二叉树的前序遍历、中序遍历
-
- 2.5.1.1 递归
- 2.5.1.2 迭代
- 2.5.2 二叉树的锯齿形层序遍历、二叉树的层序遍历 II
- 2.5.3 二叉树的最大深度、最小深度
- 三、二叉搜索树`Binary Search Tree`
-
- 3.1 二叉搜索树BST的性质
- 3.2 二叉搜索树的实现
-
- 3.2.1 `TreeNode`类
- 3.2.2 `BinarySearchTree`类
- 3.3 平衡二叉搜索AVL树
-
- 3.3.1 平衡二叉搜索树的定义
- 3.3.2 平衡二叉树最差情性能:
- 3.3.3 保持AVL树的平衡性质
- 3.3.4 rebalance重新平衡法:左右旋转
- 3.3.5 左旋转对平衡因子的影响:
- 3.4 ADT Map实现方法小结
- 四、 二叉搜索树题目
-
- 4.1 验证二叉搜索树
- 4.2 二叉搜索树迭代器
- 4.3 二叉搜索树中的搜索、插入和删除
-
- 4.3.1 二叉搜索树中的搜索
- 4.3.2 二叉搜索树中的插入操作
- 4.3.3 删除二叉树中的节点
- 4.4 数据流中的第 K 大元素
- 4.5 二叉搜索树的第k大节点
-
- 4.5.1 中序递归遍历
- 4.5.2 迭代
- 4.6 二叉搜索树的最近公共祖先
- 4.7 将有序数组转换为二叉搜索树
- 4.8 平衡二叉树
参考《算法通关手册》、B站《数据结构与算法B Python版》视频
一、 树
1.1 树的定义
树(Tree):由 n≥0n \\ge 0n≥0 个节点与节点之间的边组成的有限集合。当 n=0n = 0n=0 时称为空树,当 n>0n > 0n>0 时称为非空树。
树由若干节点,以及两两连接节点的边组成,并具有以下性质:
- 其中一个节点被设定为根;
- 每个节点n(除根节点),都恰连接一条来自节点p的边,p是n的父节点;
- 每个节点从根开始的路径是唯一的。
- 如果每个节点最多有两个子节点,这样的树称为“二叉树”
之所以把这种数据结构称为「树」是因为这种数据结构看起来就像是一棵倒挂的树,也就是说数据结构中的「树」是根朝上,而叶朝下的。如下图所示。
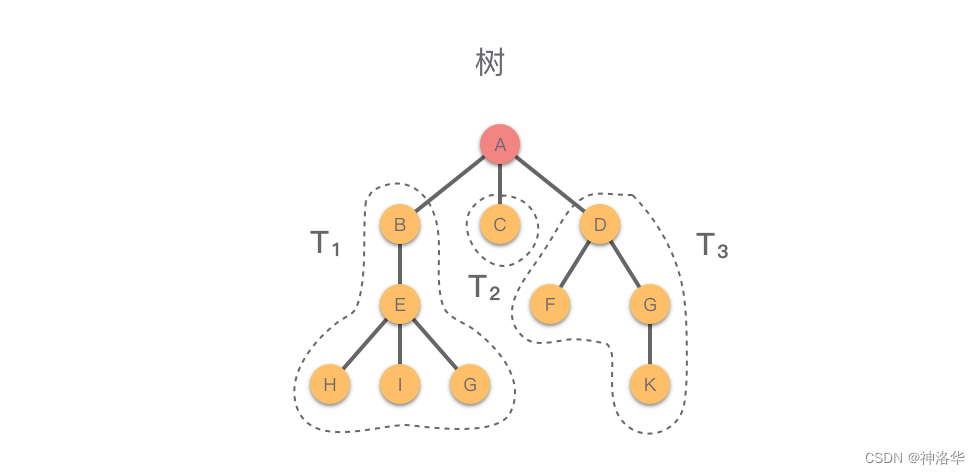
-
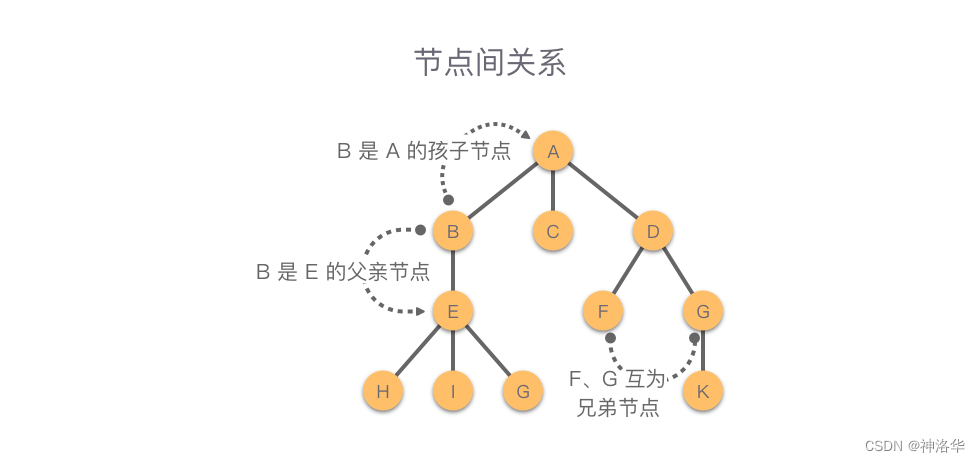
节点
Node:组成树的基本部分,每个节点具有名称,或“键值”,节点还可以保存额外数据项,数据项根据不同的应用而变。- 子节点
Children:入边均来自于同一个节点的若干节点,称为这个节点的子节点。 - 父节点
Parent:一个节点是其所有出边所连接节点的父节点。 - 兄弟节点
Sibling:具有同一个父节点的节点之间称为兄弟节点。 - 叶节点
Leaf:没有子节点的节点称为叶节点。 - 节点的度
Height:一个节点所含有的子树个数
- 子节点
-
根
Root:树中唯一一个没有入边的节点。
-
边
Edge:边是组成树的另一个基本部分。每条边恰好连接两个节点,表示节点之间具有关联,边具有出入方向;每个节点(除根节点)恰有一条来自另一节点的入边;每个节点可以有多条连到其他节点的出边。 -
路径
Path:由边依次连接在一起的节点的有序列表,例如图中E到G的路径为E - B - A - D - G。 -
路径长度:两个节点之间路径上经过的边数。例如图中
E到G的路径长度为 444。 -
子树
Subtree:一个节点和其所有子孙节点,以及相关边的集合。
如上图所示,红色节点 AAA 是根节点,除了根节点之外,还有3棵互不相交的子树 T1(B、E、H、I、G)T_1(B、E、H、I、G)T1(B、E、H、I、G)、T2(C)T_2(C)T2(C)、T3(D、F、G、K)T_3(D、F、G、K)T3(D、F、G、K)。 -
层级
Level:从根节点开始到达一个节点的路径,所包含的边的数量,称为这个节点的层级。根节点层级为0。 -
高度
height:树中所有节点的最大层级称为树的高度。
除了上面树的集合定义(树是由节点和边组成的集合),还有一种递归的定义,树是:
- 空集
- 或者由根节点和0或多个子树构成。每个子树的根节点都跟树的根节点有边相连
1.2 二叉树
树根据节点的子树是否可以互换位置,可以分为有序树和无序树,二叉树是有序树的一种。
- 有序树:节点的各个⼦树从左⾄右有序, 不能互换位置。
- 二叉树(Binary Tree):树中各个节点的度不大于
2个的有序树,称为二叉树。
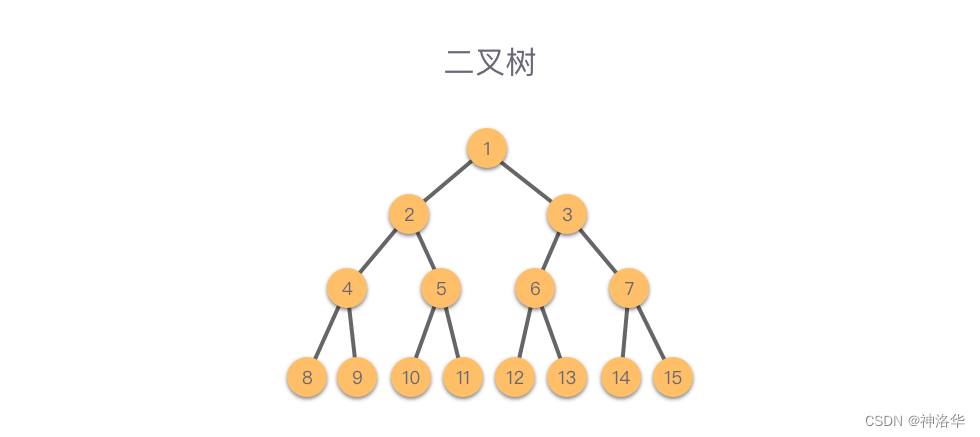
- 二叉树(Binary Tree):树中各个节点的度不大于
- 无序树:节点的各个⼦树可互换位置。
二叉树是种特殊的树(可以是空树),它最多有两个⼦树,分别为左⼦树和右⼦树,并且两个子树是有序的,不可以互换。也就是说,在⼆叉树中不存在度⼤于 222 的节点。
二叉树在逻辑上可以分为 5种基本形态,如下图所示:
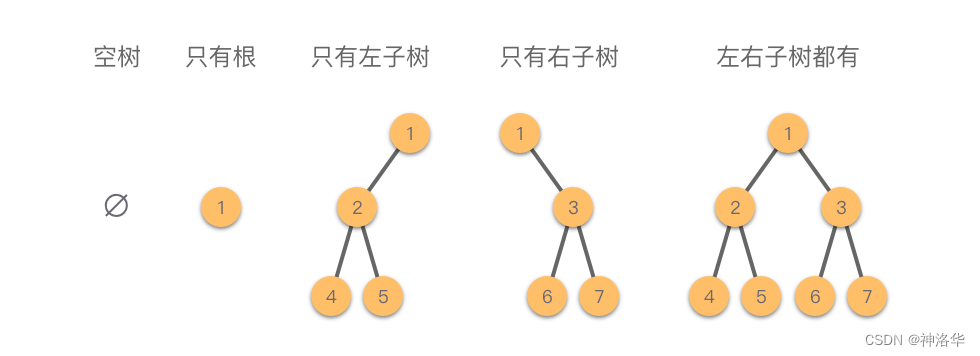
下面我们来介绍一些特殊的二叉树。
1.2.1 完全二叉树
完全二叉树(Complete Binary Tree):如果叶子节点只能出现在最下面两层,并且最下层的叶子节点都依次排列在该层最左边的位置上,具有这种特点的二叉树称为完全二叉树。
完全二叉树满足以下特点:
- 叶子节点只能出现在最下面两层。
- 每个内部节点都有两个子节点,最多只有一个内部节点例外。
- 最下层的叶子节点连续集中在最左边的位置上,即不存在只有右子树的情况。倒数第二层如果有叶子节点,则该层的叶子节点一定集中在右边的位置上。
- 同等节点数的二叉树中,完全二叉树的深度最小。
下面来看几个例子:

优先队列为了保持入队和出队复杂度都是O(logn)O(logn)O(logn),所以采用完全二叉树来实现,下文优先队列会讲到。
为了使堆操作能保持在对数水平上,就必须采用二叉树结构。同时如果要使操作始终保持在对数数量级上,就必须始终保持二叉树的平衡,树根左右子树拥有相同数量的节点,所以考虑采用完全二叉树的结构来近似实现平衡。
1.2.1 满二叉树
满二叉树(Full Binary Tree):如果所有分支节点都存在左子树和右子树,并且所有叶子节点都在同一层上,则称该二叉树为满二叉树。
满二叉树满足以下特点:
- 叶子节点只出现在最下面一层。
- 非叶子节点的度一定为 222。
- 在同等深度的二叉树中,满二叉树的节点个数最多,叶子节点个数最多。
如果我们对满二叉树的节点进行编号,根结点编号为 111,然后按照层次依次向下,每一层从左至右的顺序进行编号。则深度为 kkk 的满二叉树最后一个节点的编号为 2k−12^k - 12k−1。

1.2.3 二叉堆
堆(Heap):符合以下两个条件之一的完全二叉树:
- 大顶堆:根节点值 ≥ 子节点值。
- 小顶堆:根节点值 ≤ 子节点值。
完全二叉树中,只规定了元素插入的方式,没有按照元素值的大小规定其在树中的顺序。二叉堆是按照一定的堆次序Heap Order 排列的完全二叉树,分为两种:
- 最小堆
min heap(小顶堆):任何一个父节点的key都要小于其所有子节点的key,如下图二; - 最大堆
max heap(大顶堆):任何一个父节点的key都要大于其所有子节点的key,如下图一。
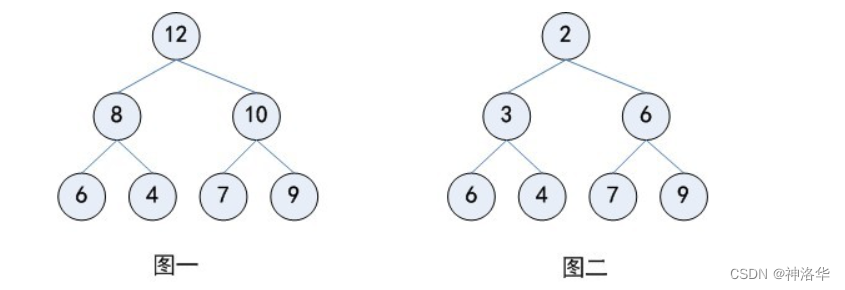
二叉堆中,任何一条路径,均是一个已排序数列,所以是部分有序。
1.2.4 二叉搜索树
二叉搜索树(Binary Search Tree):也叫做二叉查找树。二叉搜索树中,所有左子树上的节点都小于其根节点的值,所有右子树上的节点的值都大于其根节点的值,即恒有root.left.val<root.val<root.right.val。如下图所示,这 333 棵树都是二叉搜索树。

- 中序遍历BST,得到的是升序数组。中序倒序遍历,会得到一个降序数组
- 最小值一定在根节点的最左下角(中序遍历的起点),最大值一定在根节点的最右下角(中序遍历的终点)
1.2.5 平衡二叉搜索树
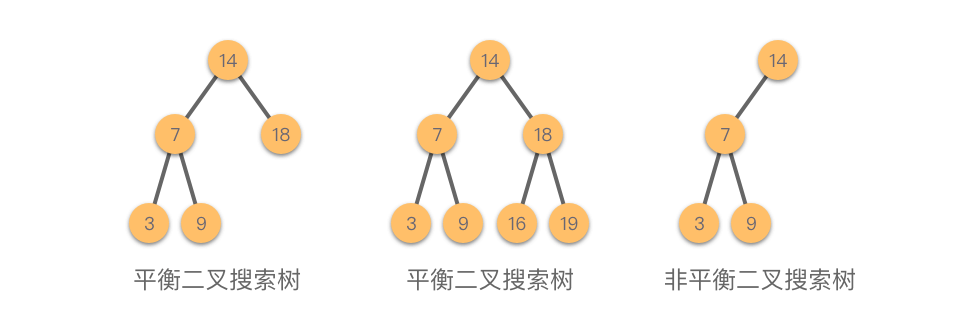
平衡二叉搜索树(Balanced Binary Tree):一种结构平衡的二叉搜索树。即叶节点高度差的绝对值不超过 111,并且左右两个子树都是一棵平衡二叉搜索树。平衡二叉树可以在 O(logn)O(logn)O(logn) 内完成插入、查找和删除操作。最早被发明的平衡二叉搜索树为 「AVL 树(Adelson-Velsky and Landis Tree))」。
AVL 树满足以下性质:
- 空二叉树是一棵 AVL 树。
- 如果 T 是一棵 AVL 树,那么其左右子树也是 AVL 树,并且 ∣h(ls)−h(rs)∣≤1|h(ls) - h(rs)| \\le 1∣h(ls)−h(rs)∣≤1,h(ls)h(ls)h(ls) 是左子树的高度,h(rs)h(rs)h(rs) 是右子树的高度。
- AVL 树的高度为 O(logn)O(log n)O(logn)。
如图所示,前 222 棵树是平衡二叉搜索树,最后一棵树不是平衡二叉搜索树,因为这棵树的左右子树的高度差的绝对值超过了 111。
1.3 二叉树的实现
1.3.1 嵌套列表法(顺序存储)
可以使用Python List来实现二叉树数据结构。
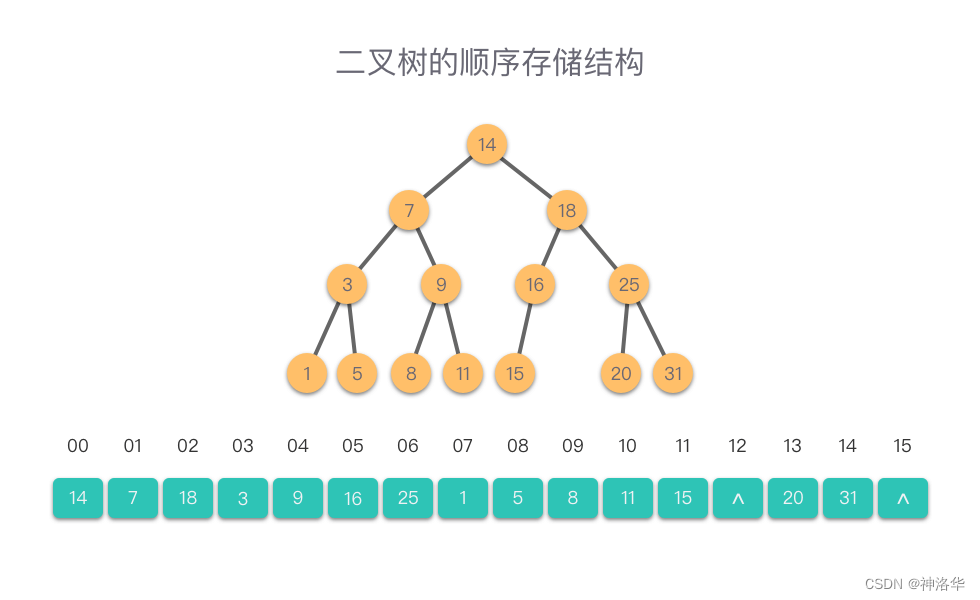
- 递归的嵌套列表实现二叉树,由具有3个元素的列表实现:
[root, left, right],这里left和right指的是左子树和右子树,所以是一个递归的表示。- 第1个元素为根节点的值;
- 第2个元素是左子树(所以也是一个列表);
- 第3个元素是右子树(所以也是一个列表);
- 叶节点没有子节点,其子树是一个空列表
- 对于二叉树,根是
myTree[0],左子树myTree[1],右子树myTree[2]。 - 嵌套列表法的优点:子树的结构与树相同,是一种递归数据结构;很容易扩展到多叉树,仅需要增加列表元素即可。

嵌套列表法代码:
def BinaryTree(r): # 创建仅有根节点的二叉树return [r, [], []]# insertLeft是在root上插入新的左子树
def insertLeft(root,newBranch): # 将新节点插入树中作为其直接的左子节点t = root.pop(1) # 将左子树pop出来,赋值给变量tif len(t) > 1: # 长度大于1表示原先就有左子树root.insert(1,[newBranch,t,[]]) # 新子树的根就是newbranch,新子树的左子树就是原先的左子树,右子树是空。else:root.insert(1,[newBranch,[],[]])# 左右子树都是空,不需要继承原先左子树return rootdef insertRight(root,newBranch): # 将新节点插入树中作为其直接的右子节点t = root.pop(2)if len(t) > 1:root.insert(2,[newBranch,[],t])else:root.insert(2, [newBranch, [], []])return rootdef getRootVal(root): # 取得根节点的值return root[0]def setRootVal(root,newVal): # 重设根节点的值root[0] = newValdef getLeftChild(root): # 返回左子树return root[1]def getRightChild(root): # 返回右子树return root[2]
代码运行示例:


对于完全二叉树(尤其是满二叉树)来说,采用顺序存储结构比较合适,它能充分利用存储空间;而对于一般二叉树,如果需要设置很多的「空节点」,则采用顺序存储结构就会浪费很多存储空间。
由于顺序存储结构固有的一些缺陷,会使得二叉树的插入、删除等操作不方便,效率也比较低。对于二叉树来说,当树的形态和大小经常发生动态变化时,更适合采用链式存储结构。
1.3.2 节点链接法(链式存储)
二叉树采用链式存储结构时,每个链节点包含一个用于数据域 val,存储节点信息;还包含两个指针域 left 和 right,分别指向左右两个子节点。当左子节点或者右子节点不存在时,相应指针域值为空。二叉链节点结构如下图所示。

定义BinaryTree类
- 每个节点的val保存其节点的数据项(数值)
- 成员
left/right children保存指向左右子树的引用(同样是BinaryTree对象)。
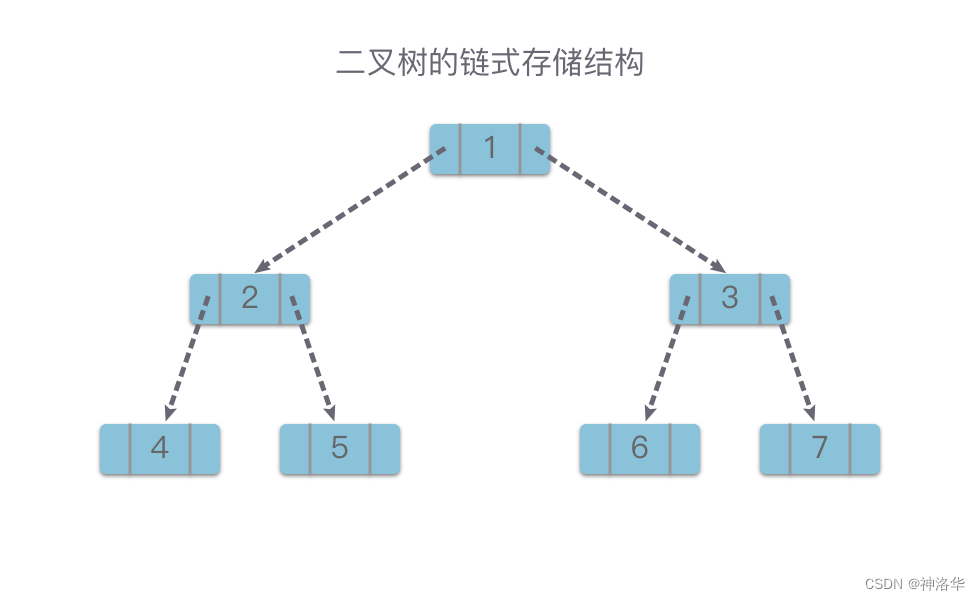
节点链接法代码:
class BinaryTree:def __init__(self,val):self.val = val # 成员val保存根节点数据项self.leftChild = None # 成员leftChild保存指向左子树的引用self.rightChild = None # 成员rightChild保存指向右子树的引用def insertLeft(self,newNode):if self.leftChild == None: # 如果原先的左子树为空self.leftChild = BinaryTree(newNode) # 将root左子树引用指向要插入的新节点else:t = BinaryTree(newNode)t.leftChild = self.leftChild # 插入节点的左子树是root的左子树self.leftChild = t # root的左子树指向插入节点def insertRight(self,newNode):if self.rightChild == None:self.rightChild = BinaryTree(newNode)else:t = BinaryTree(newNode)t.rightChild = self.rightChildself.rightChild = tdef getRightChild(self):return self.rightChilddef getLeftChild(self):return self.leftChilddef setRootVal(self,val):self.val = valdef getRootVal(self):return self.val
代码运行示例:

二叉树的链表存储结构具有灵活、方便的特点。节点的最大数目只受系统最大可存储空间的限制。一般情况下,二叉树的链表存储结构比顺序存储结构更省空间(用于存储指针域的空间开销只是二叉树中节点数的线性函数),而且对于二叉树实施相关操作也很方便,因此,一般我们使用链式存储结构来存储二叉树。
1.4 树的应用:表达式解析
- 可以将表达式表示为树结构,叶节点保存操作数,内部节点保存操作符。
- 表达式层次决定计算的优先级,越底层的表达式,优先级越高。例如全括号表达式:
((7+3)*(5-2)) - 树中的每个子树都表示一个子表达式。将子树替换为子表达式值的节点,即可实现求值。


- 从全括号表达式创建表达式解析树
-
扫描:
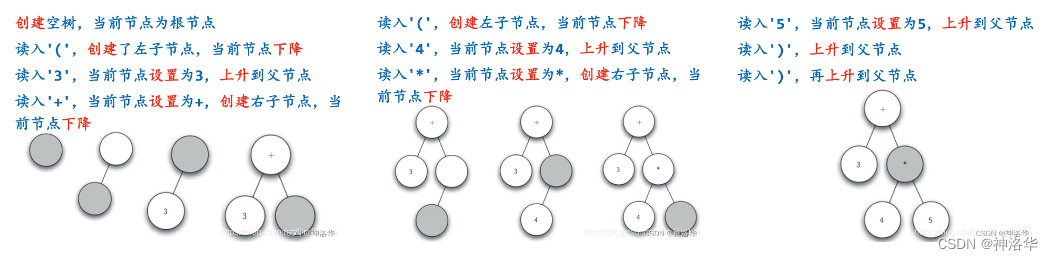
首先,全括号表达式要分解为Token列表。其单词分为括号、操作符和操作数这几类,左括号是表达式的开始,而右括号是表达式的结束。下面是一个实例演示,全括号表达式为(3+(4*5)),灰色表示当前节点:
-
归纳定义表达式解析树规则
从左到右扫描全括号表达式的每个单词,依据规则建立解析树。- 当前单词是
"(":为当前节点添加一个新节点作为其左子节点insertLeft,当前节点下降为这个新节点getLeftChild; - 当前单词是操作符
“+, -, *, /”:将当前节点的值设为此符号setRootVal,为当前节点添加一个新节点作为其右子节点insertRight,当前节点下降为这个新节点getRightChild; - 当前单词是操作数:将当前节点的值设为此数,当前节点上升到父节点;
- 当前单词是
")":则当前节点上升到父节点。
- 当前单词是
-
创建树的过程中,关键的是对当前节点的跟踪。
从上面步骤可以看到,上升到父节点目前没有支持的方法。我们可以用一个栈来记录跟踪父节点。当前节点下降时,将下降前的节点push入栈;当前节点需要上升至父节点时,上升到pop出栈的节点即可。
表达式解析树创建代码:
def buildParseTree(s):ls = s.split() # 从字符串创建token列表Stack=[] # 创建栈,存放父节点eTree = BinaryTree('') # 创建二叉树Stack.append(eTree) # 将根节点入栈,然后下降currentTree = eTreefor i in ls:if i == '(': # 表达式开始currentTree.insertLeft('') # 创建左子节点Stack.append(currentTree) # 当前节点入栈,然后下降节点currentTree = currentTree.getLeftChild() elif i not in ['+','-','*','/',')']: # 操作数currentTree.setRootVal(int(i)) currentTree = Stack.pop() # 出栈上升elif i in ['+','-','*','/']: currentTree.setRootVal(i) # 碰到操作符,将当前节点的值设为操作符currentTree.insertRight('')# 创建右子节点,当前节点入栈然后下降节点Stack.append(currentTree)currentTree = currentTree.getRightChild()elif i == ')': # 表达式结束currentTree = Stack.pop() # 出栈上升else:raise ValueError # 如果表达式中有不该出现的单词就报错return eTree
- 利用表达式解析树求值
由于二叉树BinaryTree是一个递归数据结构,自然可以用递归算法来处理。求值递归函数evaluate,可从树的底层子树开始,逐步向上层求值,最终得到整个表达式的值。
- 求值递归函数evaluate的递归三要素:
- 基本结束条件:叶节点是最简单的子树,没有左右子节点,其根节点的数据项即为子表达式树的值。
- 缩小规模:将表达式树分为左子树、右子树,即为缩小规模。
- 调用自身:分别调用evaluate计算左子树和右子树的值,然后将左右子树的值依根节点的操作符进行计算,从而得到表达式的值。
- 一个增加程序可读性的技巧:引用函数
operator。
如果使用if-else语句,判断操作符,来进行计算,随着表达式增多,可读性会变差。这里调用python内置函数operator,其包含了所有的操作符。我们将op设为+-*/这些不同的操作符,就可以使用相同的语句op(1,2)来实现不同的计算,增加代码的可读性。
import operator
op = operator.add
n = op(1,2)
表达式解析树求值代码实现:
import operator
def evaluate(parseTree):# 创建字典opers,将操作符从字符映射为具体的计算功能opers = {'+':operator.add, '-':operator.sub,'*':operator.mul, '/':operator.truediv}# 缩小规模:leftC = parseTree.getLeftChild()rightC = parseTree.getRightChild()if leftC and rightC: # 如果存在左右子树,就递归调用fn = opers[parseTree.getRootVal()] # parseTree.getRootVal()表示根节点保存的操作符return fn(evaluate(leftC),evaluate(rightC)) # 递归调用else: # 没有左右子树,就是叶节点,直接返回值就行return parseTree.getRootVal() # 基本结束条件
二、 树的遍历Tree Traversals
树的遍历:指的是从根节点出发,按照某种次序依次访问二叉树中所有节点,使得每个节点被访问一次且仅被访问一次。
树是一个递归的数据结构,所以可以按照递归您的方式进行遍历。按照对节点访问次序的不同,有4种遍历方式:
- 前序遍历(preorder):根-左-右。在遍历任何一棵子树时,都是先访问根节点,然后递归地前序遍历左子树,最后再递归地前序遍历右子树。
- 中序遍历(inorder):左-根-右。先递归地中序访问左子树,再访问根节点,最后中序访问右子树。
- 后序遍历(postorder):左-右-根。先递归地后序访问左子树,再后续访问右子树,最后访问根节点。
- 层序遍历:从根节点开始,逐层进行遍历,同一层节点则是按照从左至右的顺序依次访问。
2.1 前序遍历
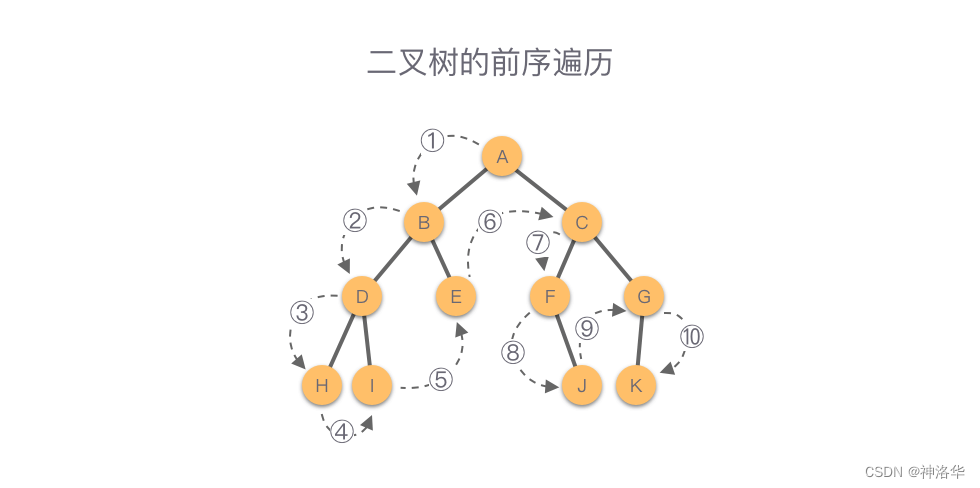
如下图所示,该二叉树的前序遍历顺序为:A - B - D - H - I - E - C - F - J - G - K。
2.1.1 前序遍历的递归实现
前序遍历递归实现代码如下:
def preorder(tree):if tree:print(tree.getRootVal()) # 访问根节点preorder(tree.getLeftChild())preorder(tree.getRightChild())
在前面构造的BinaryTree类里,实现前序遍历,需要加入子树是否为空的判断:
def preorder(self):print(self.val)if self.leftChild:self.leftChild.preorder()if self.rightChild:self.rightChild.preorder()
2.1.2 前序遍历的显式栈实现
二叉树的前序遍历递归实现的过程,实际上就是调用系统栈的过程。我们也可以使用一个显式栈 stack 来模拟递归的过程。
前序遍历的顺序为:根节点 - 左子树 - 右子树,而根据栈的「先入后出」特点,所以入栈的顺序应该为:先放入右子树,再放入左子树。这样可以保证最终遍历顺序为前序遍历顺序。 具体实现步骤如下:
- 判断二叉树是否为空,为空则直接返回。
- 初始化维护一个栈,将根节点入栈。
- 当栈不为空时:
- 弹出栈顶元素
node,并访问该元素。 - 如果
node的右子树不为空,则将node的右子树入栈。 - 如果
node的左子树不为空,则将node的左子树入栈。
- 弹出栈顶元素
二叉树的前序遍历显式栈实现代码如下:
class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root: # 二叉树为空直接返回return []res = []stack = [root]while stack: # 栈不为空node = stack.pop() # 弹出根节点res.append(node.val) # 访问根节点if node.right:stack.append(node.right) # 右子树入栈if node.left:stack.append(node.left) # 左子树入栈return res
2.2 中序遍历
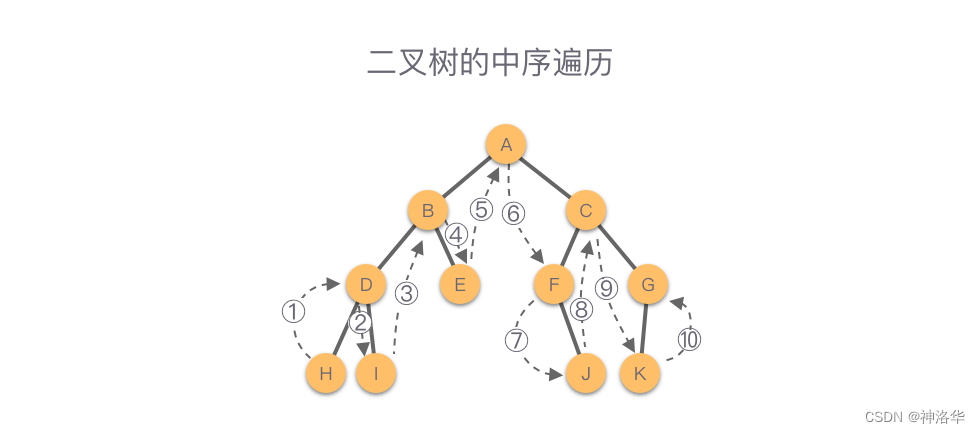
遍历任何一棵子树时仍然是按照先遍历子树根节点的左子树,然后访问根节点,最后再遍历子树根节点的右子树的顺序进行遍历。如下图所示,该二叉树的中序遍历顺序为:H - D - I - B - E - A - F - J - C - K - G。
2.2.1 中序遍历的递归实现
def inorder(tree):if tree:inorder(tree.getLeftChild())print(tree.getRootVal())inorder(tree.getRightChild())
前面1.4 章节根据全括号表达式生成了表达式解析树,反过来也可以用中序遍历的方式,从表达式解析树生成全括号表达式。
# 下面代码对每个数字也加了括号,可以进一步优化
def printexp(tree):s=''if tree:s="("+printexp(tree.getLeftChild())s=s+str(tree.getRootVal())s=s+printexp(tree.getRightChild())+")"return s
2.2.1 中序遍历的显式栈实现
与前序遍历不同,访问根节点要放在左子树遍历完之后。因此我们需要保证:在左子树访问之前,当前节点不能提前出栈。
-
先从根节点开始,循环遍历左子树,不断将当前子树的根节点放入栈中,直到当前节点无左子树时,从栈中弹出该节点并进行处理。
-
然后再访问该元素的右子树,并进行上述循环遍历左子树的操作。这样可以保证最终遍历顺序为中序遍历顺序。
二叉树的中序遍历显式栈实现步骤如下:
- 判断二叉树是否为空,为空则直接返回。
- 初始化维护一个空栈。
- 当根节点或者栈不为空时:
- 如果当前节点不为空,则循环遍历左子树,并不断将当前子树的根节点入栈。
- 如果当前节点为空,说明当前节点无左子树,则弹出栈顶元素
node,并访问该元素,然后尝试访问该节点的右子树。
二叉树的中序遍历显式栈实现代码如下:
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root: # 二叉树为空直接返回return []res = []stack = []while root or stack: # 根节点或栈不为空while root: stack.append(root) # 将当前树的根节点入栈root = root.left # 找到最左侧节点node = stack.pop() # 遍历到最左侧,当前节点无左子树时,将最左侧节点弹出res.append(node.val) # 访问该节点root = node.right # 尝试访问该节点的右子树return res
2.3 后序遍历
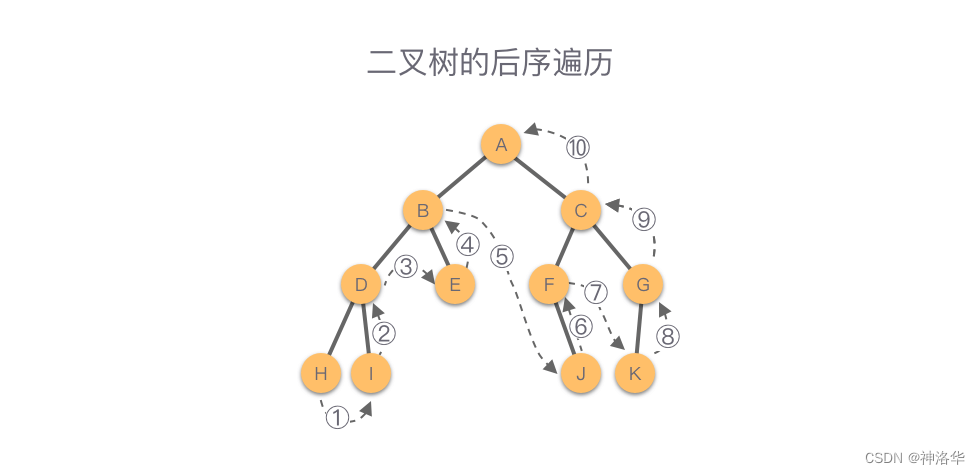
后序遍历过程也是一个递归过程。在遍历任何一棵子树时,先遍历子树根节点的左子树,然后遍历子树根节点的右子树,最后再访问根节点。如下图所示,该二叉树的后序遍历顺序为:H - I - D - E - B - J - F - K - G - C - A。
2.3.1 后序遍历的递归实现
def postorder(tree):if tree:postorder(tree.getLeftChild())postorder(tree.getRightChild())print(tree.getRootVal())
2.3.2 后序遍历的显式栈实现
与前序、中序遍历不同,在后序遍历中,根节点的访问要放在左右子树访问之后。因此,我们要保证:在左右孩子节点访问结束之前,当前节点不能提前出栈。
我们应该从根节点开始,先将根节点放入栈中,然后依次遍历左子树,不断将当前子树的根节点放入栈中,直到遍历到左子树最左侧的那个节点,从栈中弹出该元素,并判断该元素的右子树是否已经访问完毕,如果访问完毕,则访问该元素。如果未访问完毕,则访问该元素的右子树。二叉树的后序遍历显式栈实现步骤如下:
- 判断二叉树是否为空,为空则直接返回。
- 初始化维护一个空栈,使用
prev保存前一个访问的节点,用于确定当前节点的右子树是否访问完毕。 - 当根节点或者栈不为空时,从当前节点开始:
- 如果当前节点有左子树,则不断遍历左子树,并将当前根节点压入栈中。
- 如果当前节点无左子树,则弹出栈顶元素
node。 - 如果栈顶元素
node无右子树(即not node.right)或者右子树已经访问完毕(即node.right == prev),则访问该元素,然后记录前一节点,并将当前节点标记为空节点。 - 如果栈顶元素有右子树,则将栈顶元素重新压入栈中,继续访问栈顶元素的右子树。
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:res = []stack = []prev = None # 保存前一个访问的节点,用于确定当前节点的右子树是否访问完毕while root or stack: # 根节点或栈不为空while root:stack.append(root) # 将当前树的根节点入栈root = root.left # 继续访问左子树,找到最左侧节点node = stack.pop() # 遍历到最左侧,当前节点无左子树时,将最左侧节点弹出# 如果当前节点无右子树或者右子树访问完毕if not node.right or node.right == prev:res.append(node.val)# 访问该节点prev = node # 记录前一节点root = None # 将当前根节点标记为空else:stack.append(node) # 右子树尚未访问完毕,将当前节点重新压回栈中root = node.right # 继续访问右子树return res
前面1.4章节的表达式解析树求值中,其计算过程其实也是一个后序遍历的过程(左→右→根),所以可以使用后序遍历方法,重写表达式求值代码:
# 后序遍历:表达式求值
def postordereval(tree):opers = {'+':operator.add, '-':operator.sub,'*':operator.mul, '/':operator.truediv}res1 = Noneres2 = Noneif tree:res1 = postordereval(tree.getLeftChild()) # 左子树res2 = postordereval(tree.getRightChild()) # 右子树if res1 and res2:fn=opers[tree.getRootVal()]return fn(res1,res2) # 根节点else:return tree.getRootVal()
2.4 层序遍历
层序遍历步骤:
- 如果二叉树为空,则返回。
- 如果二叉树不为空,则:
- 先依次访问二叉树第
1层的节点。 - 然后依次访问二叉树第
2层的节点。 - ……
- 依次下去,最后依次访问二叉树最下面一层的节点。
- 同一层节点则是按照从左至右的顺序依次访问的
- 先依次访问二叉树第
如下图所示,该二叉树的后序遍历顺序为:A - B - C - D - E - F - G - H - I - J - K。
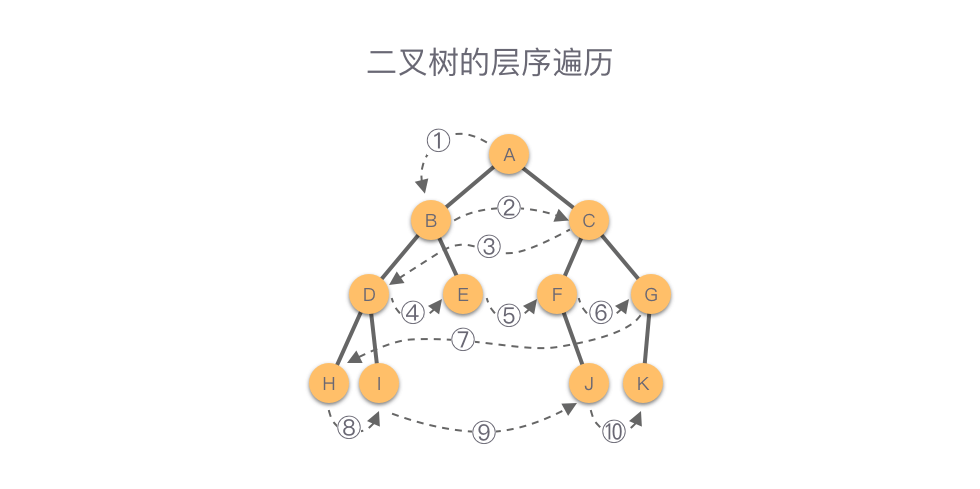
二叉树的层序遍历是通过队列来实现的。具体步骤如下:
- 判断二叉树是否为空,为空则直接返回。
- 令根节点入队。
- 当队列不为空时,求出当前队列长度 sis_isi。
- 依次从队列中取出这 sis_isi 个元素,并对这 sis_isi 个元素依次进行访问。然后将其左右子节点入队,然后继续遍历下一层节点。
- 当队列为空时,结束遍历。
二叉树的层序遍历代码实现如下:
class Solution:def levelOrder(self, root: TreeNode) -> List[List[int]]:if not root:return []queue = [root] # 根节点入队ans = []while queue: size = len(queue) # 当前队列长度 ls = [] # 当前层的临时列表for _ in range(size): cur = queue.pop(0) # 当前层节点出队ls.append(cur.val) # 将队列中的元素都拿出来(也就是获取这一层的节点),放到临时list中 # 如果节点的左/右子树不为空,也放入队列中if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right)if ls:ans.append(ls)return ans
在 while 循环的每一轮中,都是将当前层的所有结点出队列,同时将下一层的所有结点入队列,这样就实现了层序遍历

2.5 二叉树的遍历题目
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0144 | 二叉树的前序遍历 | Python | 栈、树 | 中等 |
| 0094 | 二叉树的中序遍历 | Python | 栈、树、哈希表 | 简单 |
| 0145 | 二叉树的后序遍历 | Python | 栈、树 | 简单 |
| 0102 | 二叉树的层序遍历 | Python | 树、广度优先搜索 | 中等 |
| 0103 | 二叉树的锯齿形层序遍历 | Python | 树、广度优先搜索、二叉树 | 中等 |
| 0107 | 二叉树的层序遍历 II | Python | 树、广度优先搜索 | 中等 |
| 0104 | 二叉树的最大深度 | Python | 树、深度优先搜索、递归 | 简单 |
| 0111 | 二叉树的最小深度 | Python | 树、深度优先搜索、广度优先搜索 | 简单 |
| 0124 | 二叉树中的最大路径和 | Python | 树、深度优先搜索、动态规划、二叉树 | 困难 |
| 0101 | 对称二叉树 | Python | 树、深度优先搜索、广度优先搜索 | 简单 |
| 0112 | 路径总和 | Python | 树、深度优先搜索 | 简单 |
| 0113 | 路径总和 II | Python | 树、深度优先搜索、回溯、二叉树 | 中等 |
| 0236 | 二叉树的最近公共祖先 | Python | 树 | 中等 |
| 0199 | 二叉树的右视图 | Python | 树、深度优先搜索、广度优先搜索、递归、队列 | 中等 |
| 0226 | 翻转二叉树 | Python | 树、递归 | 简单 |
| 0958 | 二叉树的完全性检验 | Python | 树、广度优先搜索、二叉树 | 中等 |
| 0572 | 另一棵树的子树 | |||
| 0100 | 相同的树 | Python | 树、深度优先搜索 | 简单 |
| 0116 | 填充每个节点的下一个右侧节点指针 | Python | 树、深度优先搜索、广度优先搜索 | 中等 |
| 0117 | 填充每个节点的下一个右侧节点指针 II | Python | 树、深度优先遍历 | 中等 |
| 0297 | 二叉树的序列化与反序列化 | Python | 树、设计 | 困难 |
| 0114 | 二叉树展开为链表 |
2.5.1 二叉树的前序遍历、中序遍历
- 0144 二叉树的前序遍历
- 0094 二叉树的中序遍历
- 题解《动画演示+三种实现 94. 二叉树的中序遍历》
下面只介绍中序遍历,因为二叉搜索树中用的较多
2.5.1.1 递归
定义 preorderTraversal(self,root) 表示当前遍历到 root 节点的答案。那么按照定义:
- 递归调用self.preorderTraversal(root.left) 来遍历 root 节点的左子树,然后将 root 节点的值加入答案
- 递归调用preorderTraversal(root.right) 来遍历 root 节点的右子树
- 递归终止的条件为碰到空节点。
递归的调用过程是不断往左边走,当左边走不下去了,就打印节点,并转向右边,然后右边继续这个过程。

# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):def __init__(self,ans=[]):self.ans=[]def preorderTraversal(self, root):""":type root: TreeNode:rtype: List[int]"""# 前序遍历顺序是根左右 if root:self.preorderTraversal(root.left) self.ans.append(root.val) self.preorderTraversal(root.right)return self.ans
2.5.1.2 迭代
递归实现时,是函数自己调用自己,一层层的嵌套下去,操作系统/虚拟机自动帮我们用 栈 来保存了每个调用的函数,现在我们需要自己模拟这样的调用过程。
class Solution(object):def inorderTraversal(self, root):""":type root: TreeNode:rtype: List[int]"""stack=[]ans=[]while stack or root:# 不断往左子树方向走,每走一次就将当前节点保存到栈中,模拟栈的调用if root:stack.append(root)root=root.left# 当前节点为空,说明左边走到头了,从栈中弹出节点并保存# 然后转向右边节点,继续上面整个过程(往左走到头再往右走到头)else:node=stack.pop()ans.append(node.val)root=node.rightreturn ans
或者是:
class Solution(object):def inorderTraversal(self, root):""":type root: TreeNode:rtype: List[int]"""stack=[]ans=[]while stack or root:# 左边走到头后开始出栈,保存结果,同时往右走。# 往右走之后,下一个节点有左子节点,就往左走,循环往复while root:stack.append(root)root=root.left root=stack.pop()ans.append(root.val)root=root.rightreturn ans
2.5.2 二叉树的锯齿形层序遍历、二叉树的层序遍历 II
- 0103二叉树的锯齿形层序遍历
- 0107二叉树的层序遍历 II
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)
示例:
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[20,9],[15,7]]
此题和 0094 二叉树的中序遍历非常相似,前者都是从左至右遍历每一层。此题只需要将每一层遍历后得到的临时元素列表ls的顺序改变一下,再添加到最终答案ans就行。
class Solution(object):def zigzagLevelOrder(self, root):""":type root: TreeNode:rtype: List[List[int]]"""if not root:return []queue = [root] # 根节点入队ans = []level=1while queue: size = len(queue) # 当前队列长度 ls = [] # 当前层的临时列表for _ in range(size): cur = queue.pop(0) # 当前层节点出队ls.append(cur.val) # 将队列中的元素都拿出来,放到临时list中 # 如果节点的左/右子树不为空,也放入队列中if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right)if ls: ans.append(ls) if level%2==1 else ans.append(ls[::-1])level+=1return ans
如果是 0107二叉树的层序遍历 II ,将ans赋值改一下就行: (如果是ans+=ls,就是正常的自顶向下层序遍历的答案)
''''''# 前面都相同,只是不要level变量if ls: ans=[ls]+ansreturn ans
2.5.3 二叉树的最大深度、最小深度
- 0104二叉树的最大深度
- 0111二叉树的最小深度
1. 二叉树的最大深度
给定一个二叉树,找出其最大深度。示例:
给定二叉树 [3,9,20,null,null,15,7],返回它的最大深度 3 。
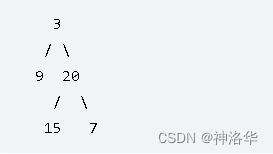
直接套用上面层序遍历的代码,遍历每一层时level+=1,最后返回level。
class Solution(object):def maxDepth(self, root):""":type root: TreeNode:rtype: int"""if not root:return 0queue = [root] # 根节点入队level=0while queue:level+=1 size = len(queue) # 当前队列长度 ls = [] # 当前层的临时列表for _ in range(size): cur = queue.pop(0) # 当前层节点出队ls.append(cur.val) # 将队列中的元素都拿出来,放到临时list中 # 如果节点的左/右子树不为空,也放入队列中if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right) return level
2. 二叉树的最小深度
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
套用层序遍历模板,当遍历到某一层,有叶节点时(没有左右子节点),返回level。
class Solution(object):def minDepth(self, root):""":type root: TreeNode:rtype: int"""if not root:return 0queue = [root] # 根节点入队level=0while queue: level+=1size = len(queue) # 当前队列长度 ls = [] # 当前层的临时列表for _ in range(size): cur = queue.pop(0) # 当前层节点出队ls.append(cur.val) # 将队列中的元素都拿出来,放到临时list中 # 如果节点的左/右子树不为空,也放入队列中if not cur.left and not cur.right:return levelelse:if cur.left:queue.append(cur.left)if cur.right:queue.append(cur.right)return level
文章目录
-
- 一、 树
-
- 1.1 树的定义
- 1.2 二叉树
-
- 1.2.1 完全二叉树
- 1.2.1 满二叉树
- 1.2.3 二叉堆
- 1.2.4 二叉搜索树
- 1.2.5 平衡二叉搜索树
- 1.3 二叉树的实现
-
- 1.3.1 嵌套列表法(顺序存储)
- 1.3.2 节点链接法(链式存储)
- 1.4 树的应用:表达式解析
- 二、 树的遍历Tree Traversals
-
- 2.1 前序遍历
-
- 2.1.1 前序遍历的递归实现
- 2.1.2 前序遍历的显式栈实现
- 2.2 中序遍历
-
- 2.2.1 中序遍历的递归实现
- 2.2.1 中序遍历的显式栈实现
- 2.3 后序遍历
-
- 2.3.1 后序遍历的递归实现
- 2.3.2 后序遍历的显式栈实现
- 2.4 层序遍历
- 2.5 二叉树的遍历题目
-
- 2.5.1 二叉树的前序遍历、中序遍历
-
- 2.5.1.1 递归
- 2.5.1.2 迭代
- 2.5.2 二叉树的锯齿形层序遍历、二叉树的层序遍历 II
- 2.5.3 二叉树的最大深度、最小深度
- 三、二叉搜索树`Binary Search Tree`
-
- 3.1 二叉搜索树BST的性质
- 3.2 二叉搜索树的实现
-
- 3.2.1 `TreeNode`类
- 3.2.2 `BinarySearchTree`类
- 3.3 平衡二叉搜索AVL树
-
- 3.3.1 平衡二叉搜索树的定义
- 3.3.2 平衡二叉树最差情性能:
- 3.3.3 保持AVL树的平衡性质
- 3.3.4 rebalance重新平衡法:左右旋转
- 3.3.5 左旋转对平衡因子的影响:
- 3.4 ADT Map实现方法小结
- 四、 二叉搜索树题目
-
- 4.1 验证二叉搜索树
- 4.2 二叉搜索树迭代器
- 4.3 二叉搜索树中的搜索、插入和删除
-
- 4.3.1 二叉搜索树中的搜索
- 4.3.2 二叉搜索树中的插入操作
- 4.3.3 删除二叉树中的节点
- 4.4 数据流中的第 K 大元素
- 4.5 二叉搜索树的第k大节点
-
- 4.5.1 中序递归遍历
- 4.5.2 迭代
- 4.6 二叉搜索树的最近公共祖先
- 4.7 将有序数组转换为二叉搜索树
- 4.8 平衡二叉树
参考《算法通关手册》、B站《数据结构与算法B Python版》视频
三、二叉搜索树Binary Search Tree
3.1 二叉搜索树BST的性质
二叉搜索树(二叉查找树):比父节点小的key都出现在左子树,比父节点大的key都出现在右子树,即恒有root.left.val<root.val<root.right.val。
- 中序遍历BST,得到的是升序数组。中序倒序遍历,会得到一个降序数组
- 最小值一定在根节点的最左下角(中序遍历的起点),最大值一定在根节点的最右下角(中序遍历的终点)
下图是 按照[70,31,93,94,14,23,73]的顺序插入生成的BST。注意:插入顺序不同,生成的BST也不同。
3.2 二叉搜索树的实现
二叉搜索树可以通过构造TreeNode和BinarySearchTree两个类来实现。
3.2.1 TreeNode类
__iter__:python中使用__iter__方法来实现for循环的迭代。在TreeNode类中重写iter迭代器之后,就可以使用for循环来枚举二叉树中所有的key。- 代码中使用中序遍历的方法实现二叉树的遍历迭代
- 迭代器当中,必须要使用
yield语句,每次调用yield都返回一次迭代之后的返回值(elem)。 - 在
BinarySearchTree中,直接调用TreeNode的__iter__方法进行迭代。
findSuccessor:找到当前节点的后继节点(当前节点的右子树中最小的节点),此方法在BinarySearchTree类的节点删除方法中会调用到。spliceOut:将当前节点摘除(将其子节点直接指向其父节点,跳过当前节点并返回)
mytree=BinarySearchTree()
for key,value in mytree:print(key,value)
class TreeNode:def __init__(self,key,val,left=None,right=None,parent=None):self.key = key # 键值self.payload = val # 数据项self.leftChild = left # 左子节点self.rightChild = right # 右子节点self.parent = parent # 父节点def hasLeftChild(self): # 是否含有左子节点return self.leftChilddef hasRightChild(self):return self.rightChilddef isLeftChild(self): # 是否是左子节点return self.parent and self.parent.leftChild == selfdef isRightChild(self):return self.parent and self.parent.rightChild == selfdef isRoot(self): # 是否是根节点return not self.parentdef isLeaf(self): # 是否是叶节点return not (self.rightChild or self.leftChild)def hasAnyChildren(self): # 是否有左子节点return self.rightChild or self.leftChilddef hasBothChildren(self): # 是否有右子节点return self.rightChild and self.leftChilddef replaceNodeData(self,key,value,lc,rc):self.key = keyself.payload = valueself.leftChild = lcself.rightChild = rcif self.hasLeftChild():self.leftChild.parent = selfif self.hasRightChild():self.rightChild.parent = selfdef findSuccessor(self): # 寻找当前节点的后继节点succ = Noneif self.hasRightChild(): succ = self.rightChild.findMin() # 后继节点是当前节点右子树中最小的节点# 下面这段代码是当前节点没有右子树的情况,这样后继节点就要到其它地方去寻找# BinarySearchTree中,被删节点有两个子节点时才需要找其后继节点,所以这段代码不会用到else: if self.parent:if self.isLeftChild():succ = self.parentelse:self.parent.rightChild = Nonesucc = self.parent.findSuccessor()self.parent.rightChild = selfreturn succdef findMin(self): current = selfwhile current.hasLeftChild(): # 当前子树的最小节点,沿着当前节点一直往左找就行current = current.leftChildreturn currentdef spliceOut(self): # 摘除后继节点if self.isLeaf(): # 如果是叶节点,直接摘除if self.isLeftChild(): self.parent.leftChild = Noneelse:self.parent.rightChild = Noneelif self.hasAnyChildren(): # 这一段不会用到,因为后继节点是被删节点右子树的左下角,不可能还有左子树if self.hasLeftChild():if self.isLeftChild():self.parent.leftChild = self.leftChildelse:self.parent.rightChild = self.leftChildself.leftChild.parent = self.parentelse: # 后继节点可能还有右子节点if self.isLeftChild():self.parent.leftChild = self.rightChild # 摘出带右子节点的后继节点else: # 这个也不会用到,后继节点只可能是左子节点self.parent.rightChild = self.rightChildself.rightChild.parent = self.parentdef __iter__(self): # 以中序遍历的方式迭代BST中的每一个keyif self:if self.hasLeftChild():for elem in self.leftChild:yield elemyield self.keyif self.hasRightChild():for elem in self.rightChild:yield elem
3.2.2 BinarySearchTree类
put(key,val)方法:插入key构造BST。- 首先看BST是否为空,如果一个节点都没有,那么key成为根节点root;
- 如果不是空树,就调用一个递归函数
_put(key, val, root)来放置key。
_put(key,val,self.root)的流程:- 如果key比当前节点currentNode小,那么递归_put到左子树。但如果没有左子树,那么key就成为左子节点;
- 如果key比currentNode大,那么递归_put到右子树,但如果没有右子树,那么key就成为右子节点。
- 下图显示在一个BST中插入新的节点19,每次插入操作都是从根节点开始进行比较,灰色表示当前节点。

__setitem__:python内置的索引赋值特殊方法,重写之后可以直接进行索引赋值,例如:
def __setitem__(self, k, v): self.put(k,v) # 调用put方法重写内置的索引赋值函数mytree=BinarySearchTree()
mytree[3]='red' # 插入节点3,值为'red'
-
__getitem__:python内置函数,用于索引取值,例如输入mytree[3],可以返回’red’。 -
__contains__:python内置函数,用于调用in函数。in函数对应__contains__方法。 -
get方法:在树中找到key所在的节点并返回它的值。- 如果是空树,直接返回None
- 不是空树,递归地调用
self._get找到节点key。
-
delete方法:删除节点。- 用
_get方法找到要删除的节点,然后调用remove来删除,找不到则提示错误。 - 从BST中remove一个节点,还要求仍然保持BST的性质,分以下三种情况:这个节点没有子节点;这个节点有1个子节点;这个节点有2个子节点。
-
当前节点是叶节点,则直接删除。判断其是叶节点之后,在判断其是左子节点还是右子节点,然后将其父节点的左子节点或者右子节点指向None就行。
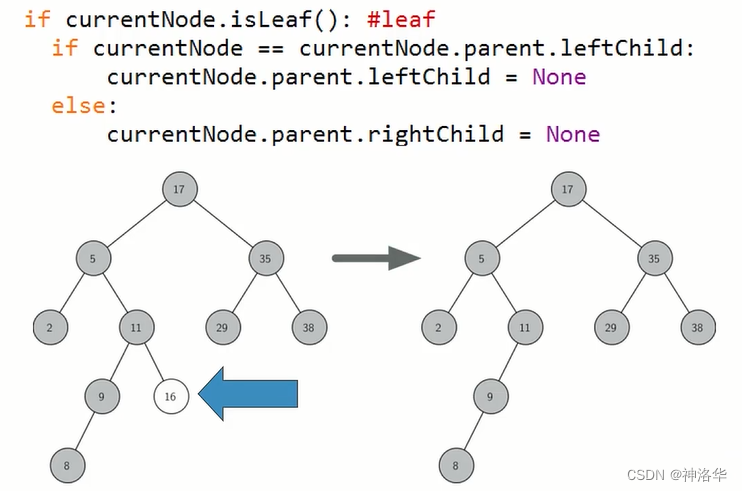
-
被删节点有1个子节点,解决方法:将这个唯一的子节点上移,替换掉被删节点的位置。实际中要分好几种情况。

-
被删节点有2个子节点。这时无法简单地将某个子节点上移替换被删节点。但可以找到另一个合适地节点来替换被删节点,这个合适节点就是被删节点的下一个key值节点,即被删节点右子树中最小的那个,称为后继节点。(当前节点右子树中最左下角叶节点)

-
- 用
-
__delitem__:这是del函数的调用方法,重写之后,可以使用del语句删除节点。
代码实现:
class BinarySearchTree:def __init__(self):self.root = Noneself.size = 0def length(self):return self.sizedef __len__(self):return self.sizedef __iter__(self):return self.root.__iter__()def put(self,key,val):# 不为空,则递归调用 self._put函数,其参数self.root表示以哪个为作为根节点进行插入 if self.root:self._put(key,val,self.root) else:self.root = TreeNode(key,val) # 如果树为空,则将其直接作为根节点self.size = self.size + 1def _put(self,key,val,currentNode): # 如果key比当前节点小,递归地放到其左子树,如果没有左子树,就直接作为其左子节点 if key < currentNode.key:if currentNode.hasLeftChild():self._put(key,val,currentNode.leftChild) # 递归插入左子树else:currentNode.leftChild = TreeNode(key,val,parent=currentNode)else:if currentNode.hasRightChild():self._put(key,val,currentNode.rightChild) # 递归插入右子树else:currentNode.rightChild = TreeNode(key,val,parent=currentNode)def __setitem__(self, k, v): # 重写索引赋值方法self.put(k,v)def get(self,key):if self.root:res = self._get(key,self.root) # 递归地查找keyif res:return res.payload # 找到节点则返回值else:return None # 没找到返回Noneelse:return None # 空树直接返回Nonedef _get(self,key,currentNode):#递归到最后都没找到,返回Noneif not currentNode: return Noneelif currentNode.key == key: # 如果要找的key正好是当前节点,直接返回return currentNodeelif key < currentNode.key: # 如果key小于当前节点的key,就递归地到其左子树中去找return self._get(key,currentNode.leftChild)else:return self._get(key,currentNode.rightChild)def __getitem__(self, key): # python内置的索引取值函数return self.get(key)def __contains__(self, key): # python内置的in函数if self._get(key,self.root):return Trueelse:return Falsedef delete(self, key):if self.size > 1: # 判断是否只剩下根节点nodeToRemove = self._get(key, self.root) # 查找待删除节点if nodeToRemove: # 如果找到了,就执行删除操作self.remove(nodeToRemove)self.size = self.size - 1else:raise KeyError('Error, key not in tree')# 如果只剩下根节点,且就是要删的key,就将根节点的引用指向Noneelif self.size == 1 and self.root.key == key: self.root = Noneself.size = self.size - 1else:raise KeyError('Error, key not in tree')def __delitem__(self,key):self.delete(key)def remove(self,currentNode):if currentNode.isLeaf(): # 被删节点是叶节点if currentNode == currentNode.parent.leftChild:currentNode.parent.leftChild = Noneelse:currentNode.parent.rightChild = Noneelif currentNode.hasBothChildren(): # 被删节点有两个子节点succ = currentNode.findSuccessor() # 找到被删节点的后继节点succ.spliceOut() # 摘出后继节点currentNode.key = succ.key # 将当前节点的key替换为后继节点的keycurrentNode.payload = succ.payloadelse: # 被删节点只有一个子节点if currentNode.hasLeftChild(): # 被删节点只有左子节点if currentNode.isLeftChild(): # 被删的也是左子节点currentNode.leftChild.parent = currentNode.parentcurrentNode.parent.leftChild = currentNode.leftChildelif currentNode.isRightChild(): # 被删的是右子节点currentNode.leftChild.parent = currentNode.parentcurrentNode.parent.rightChild = currentNode.leftChildelse: # 根节点删除currentNode.replaceNodeData(currentNode.leftChild.key,currentNode.leftChild.payload,currentNode.leftChild.leftChild,currentNode.leftChild.rightChild)else:if currentNode.isLeftChild(): # 左子节点删除currentNode.rightChild.parent = currentNode.parentcurrentNode.parent.leftChild = currentNode.rightChildelif currentNode.isRightChild(): # 右子节点删除currentNode.rightChild.parent = currentNode.parentcurrentNode.parent.rightChild = currentNode.rightChildelse: # 根节点删除currentNode.replaceNodeData(currentNode.rightChild.key,currentNode.rightChild.payload,currentNode.rightChild.leftChild,currentNode.rightChild.rightChild)
3.3 平衡二叉搜索AVL树
二叉搜索树复杂度分析(以 put 为例)
put操作的性能,决定因素在于二叉搜索树的高度(最大层次),而其高度又受数据项 key 插入顺序的影响。- 如果 key是随机分布的话,那么大于和小于根节点 key 的键值大致相等, BST 的高度就是 log2Nlog_{2}Nlog2N ( N是节点的个数),这样的树就是平衡树。
- 当key是升序或降序排列时,每次都插入到当前节点的右子树/左子树。此时二叉树类似一个单链表,其put 方法性能最差,为O(ln)O (ln)O(ln)。

如何改进BST,使其不受key列表顺序的影响?由此就引入了平衡二叉树(AVL树,发明者名字的缩写)。
3.3.1 平衡二叉搜索树的定义
平衡二叉树能在key插入时一直保持平衡。其代码结构和BST类似,只是生成和维护的过程不一样。
- 平衡二叉树的实现中,需要对每个节点跟踪平衡因子
balance factor。 - 平衡因子是根据节点的左右子树的高度来定义的,确切地说,是左右子树的高度差:
balanceFactor = height(leftSubTree) - height(rightSubTree)。如果平衡因子大于0,称为左重left-heavy,小于零称为右重right-heavy,平衡因子balanceFactor=0,则称作平衡。 - 如果一个二叉搜素树中每个节点的平衡因子都在-1, 0, 1之间,则把这个二叉搜索树称为平衡树。
在平衡树操作过程中,有节点的平衡因子超出此范围,则需要一个重新平衡的过程。

3.3.2 平衡二叉树最差情性能:
AVL树要求平衡因子为1或者-1。下图为平衡因子为1的左重AVL树,树的高度从1开始,来看看问题规模(总节点数N)和比对次数(树的高度h)之间的关系如何。
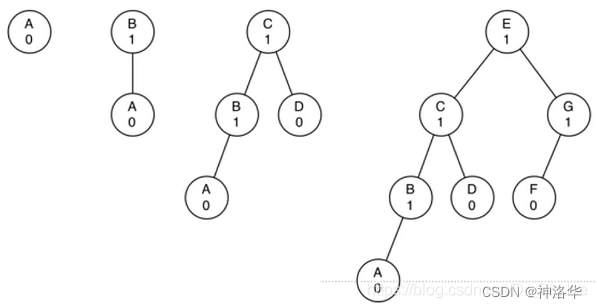
观察上图h = 1~4时,总节点数N的变化:
h = 1, N = 1
h = 2, N = 2 = 1+ 1
h = 3, N = 4 = 1 + 1 + 2
h = 4, N = 7 = 1 + 2 + 4
可得通式:Nh=1+Nh−1+Nh−2N_h = 1 + N_{h-1} + N_{h-2}Nh=1+Nh−1+Nh−2 ,观察这个通式,很接近斐波那契。

3.3.3 保持AVL树的平衡性质
- 首先,作为BST,新key必定以叶节点形式插入到AVL树中。
- 叶节点的平衡因子是0,其本身无需重新平衡,但会影响其父节点的平衡因子:作为左子节点插入,则父节点平衡因子会增加1;作为右子节点插入,则父节点平衡因子会减少1.
- 这种影响可能随着其父节点到根节点的路径一直传递上去,直到:传递到根节点为止;或者某个父节点的平衡因子被调整到0,不再影响上层节点的平衡因子为止。
AVL树相比BST只需要调整put方法就行。当插入节点作为左子节点或者右子节点时有个调整平衡因子的过程
- 第一个if:只要节点的平衡因子不在-1到1就要再次调用自己来平衡。
- 如果插入节点是父节点的左子节点就+1,是右子节点就-1
- 最后一个if:如果父节点调整后还不为0就继续往上调整。


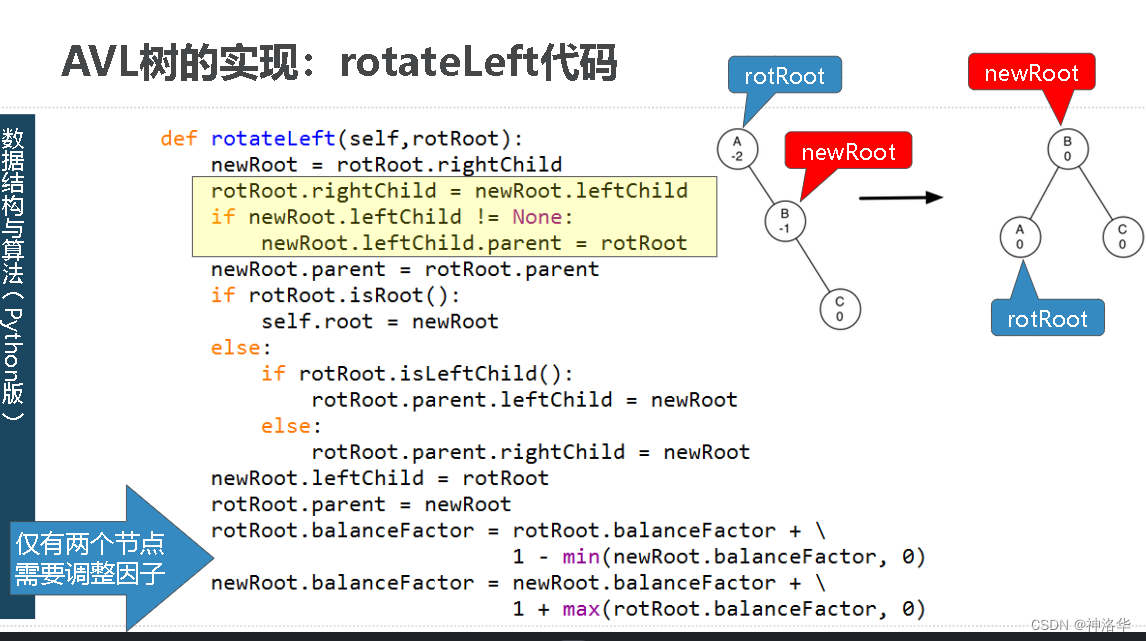
3.3.4 rebalance重新平衡法:左右旋转
-
主要手段:将不平衡的子树进行旋转
rotation。视左重或者右重进行不同方向的旋转,同时更新相关父节点引用,更新旋转后被影响节点的平衡因子。
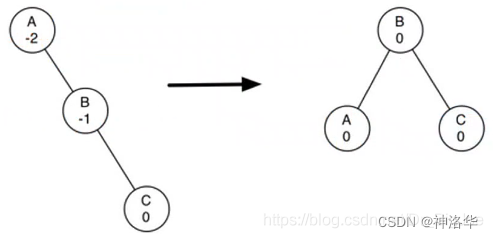
-
如上图,是一个右重子树A的左旋转(并保持BST性质)。将右子节点B提升为子树的根,将旧根节点A作为新根节点B的左子节点;如果新根节点B原来有左子节点,则将此节点设置为A的右子节点(A的右子节点一定有空)。
-
更复杂的情况:如下图左重的子树右旋转。旋转后,新根节点将旧根节点作为右子节点,但是新根节点原来已有右子节点,需要将原有的右子节点重新定位;原有的右子节点D改到旧根节点E的左子节点,同样,E的左子节点在旋转后一定有空。
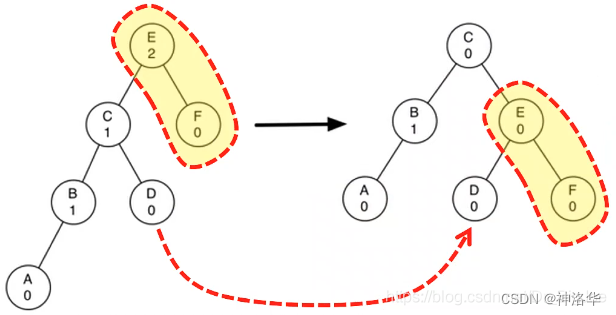
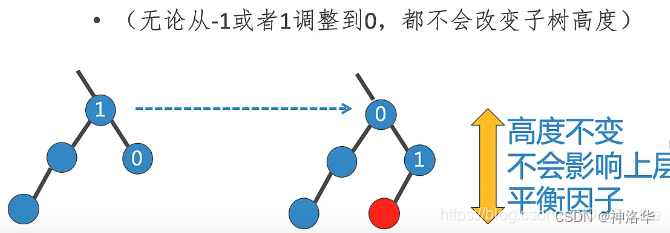
3.3.5 左旋转对平衡因子的影响:
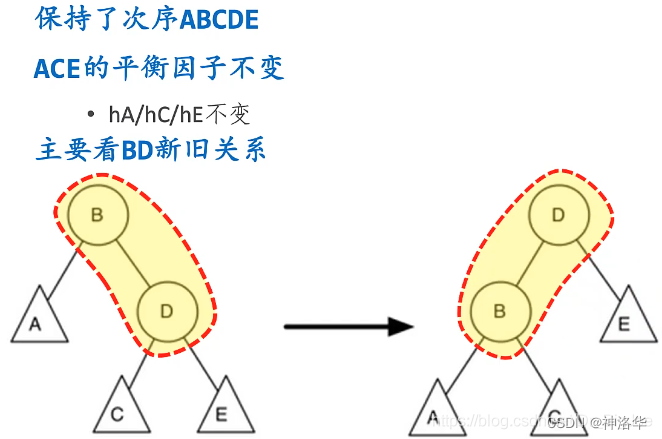
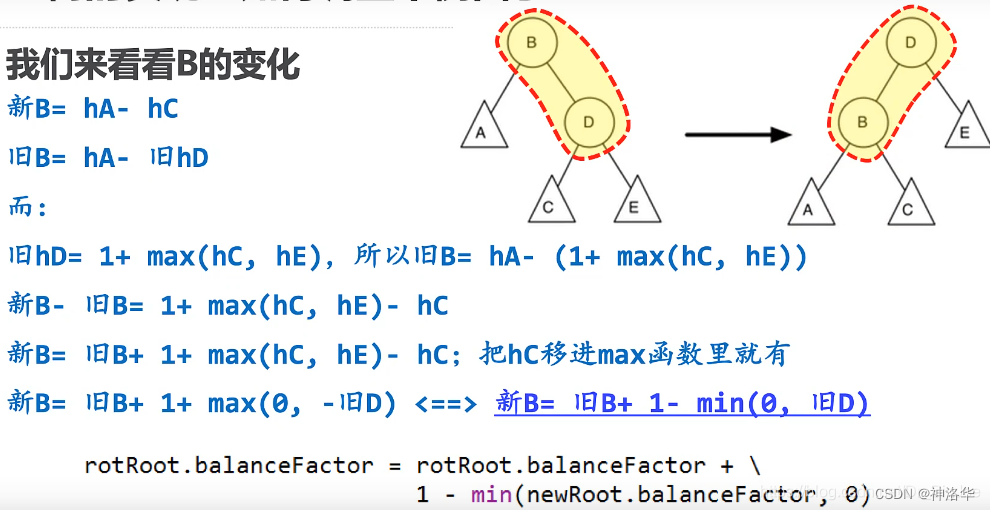
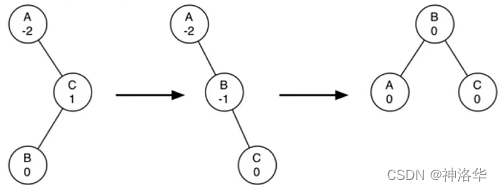
下图右重子树,单纯的左旋转无法实现平衡,左旋转后变成左重了,左重再右旋转,还回到右重。

所以,在左旋转之前检查右子节点的因子,如果右子节点左重的话,先对它进行右旋转,再实施原来的左旋转;同样,在右旋转之前检查左子节点的因子,如果左子节点右重的话,先对它进行左旋转,再实施原来的右旋转。

AVL树算法代价:
- 经过复杂的put方法,AVL树始终维持平衡,get方法也始终保持O(logn)O(logn)O(logn)高性能。
- 将AVL树的put方法分为两个部分:
- 需要插入的新节点是叶节点,更新其所有父节点和祖先节点的代价最多为O(logn)O(logn)O(logn)
- 如果插入的新节点引发了不平衡,重新平衡最多需要两次旋转,但旋转的代价与问题规模无关,旋转代价是常数O(1)O(1)O(1)。所以整个put方法的时间复杂度还是O(logn)O(logn)O(logn)。
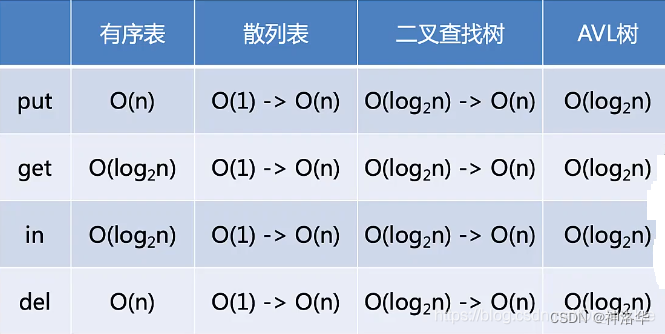
3.4 ADT Map实现方法小结
推荐使用散列表和AVL树。
-
有序表插入需要按顺序找到位置,所以是O(n)O(n)O(n),查找时可以使用二分查找,所以是O(logn)O(logn)O(logn),in和get一样的二分查找。
-
散列表:根据散列函数计算每个值应该呆的地方,一般情况下是O(1)O(1)O(1)的。因为散列冲突,最坏情况退化到O(n)O(n)O(n)
-
二叉搜素树:各种操作一般都是O(logn)O(logn)O(logn),但是随着插入顺序的而不同,极端情况会退化到线性表O(n)O(n)O(n)
当对内存和计算时间要求不高的时候可以用散列表,其次是AVL数。python内置的字典就是散列表实现的。
四、 二叉搜索树题目
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0098 | 验证二叉搜索树 | Python | 树、深度优先搜索、递归 | 中等 |
| 0173 | 二叉搜索树迭代器 | Python | 栈、树、设计 | 中等 |
| 0700 | 二叉搜索树中的搜索 | Python | 树 | 简单 |
| 0701 | 二叉搜索树中的插入操作 | Python | 树 | 中等 |
| 0450 | 删除二叉搜索树中的节点 | Python | 树 | 中等 |
| 0703 | 数据流中的第 K 大元素 | Python | 树、设计、二叉搜索树、二叉树、数据流、堆(优先队列) | 简单 |
| 剑指 Offer 54 | 二叉搜索树的第k大节点 | Python | 树、深度优先搜索、二叉搜索树、二叉树 | 简单 |
| 0230 | 二叉搜索树中第K小的元素 | |||
| 0235 | 二叉搜索树的最近公共祖先 | Python | 树 | 简单 |
| 0426 | 将二叉搜索树转化为排序的双向链表 | Python | 栈、树、深度优先搜索、二叉搜索树、链表、二叉树、双向链表 | 中等 |
| 0108 | 将有序数组转换为二叉搜索树 | Python | 树、深度优先搜索 | 简单 |
| 0110 | 平衡二叉树 | Python | 树、深度优先搜索、递归 | 简单 |
4.1 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
- 思路一:中序遍历,看结果是否是升序
根据二叉搜索树的性质可知,中序遍历二叉树,结果一定是升序。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):def __init__(self, ans=None):self.ans=[]def isValidBST(self, root):""":type root: TreeNode:rtype: bool"""if not root:return Fasleans=self.inorderTraversal(root) return ans==sorted(ans) if len(ans)==len(set(ans)) else Falsedef inorderTraversal(self, root):""":type root: TreeNode:rtype: List[int]"""# 中序遍历,类似中缀表达式,是左中右的顺序if root:self.inorderTraversal(root.left)self.ans.append(root.val)self.inorderTraversal(root.right)return self.ans
- 思路二:递归
class Solution:def isValidBST(self, root: TreeNode) -> bool:def helper(node, lower = float('-inf'), upper = float('inf')) -> bool:if not node:return Trueval = node.valif val <= lower or val >= upper:return Falseif not helper(node.right, val, upper):return Falseif not helper(node.left, lower, val):return Falsereturn Truereturn helper(root)
4.2 二叉搜索树迭代器
实现一个二叉搜索树的迭代器 BSTIterator。表示一个按中序遍历二叉搜索树(BST)的迭代器:
def __init__(self, root: TreeNode)::初始化 BSTIterator 类的一个对象,会给出二叉搜索树的根节点。def hasNext(self) -> bool::如果向右指针遍历存在数字,则返回 True,否则返回 False。def next(self) -> int::将指针向右移动,返回指针处的数字。
示例:
输入
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]
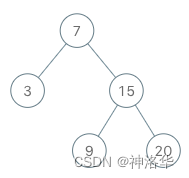
- 思路一:列表存储
初始化时就逆序遍历二叉搜索树,将结果添加到列表中。当执行next方法时,直接pop列表的最后一个元素
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = rightclass BSTIterator(object):def __init__(self, root):""":type root: TreeNode"""self.stack=[] self.inorder(root)def inorder(self, root):""":type root: TreeNode:rtype: List[int]"""# 中序遍历,类似中缀表达式,是左中右的顺序if root:self.inorder(root.right)self.stack.append(root.val)self.inorder(root.left)def next(self):""":rtype: int"""if self.stack:return self.stack.pop()def hasNext(self):""":rtype: bool"""return len(self.stack)# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()
-
思路二:迭代
中序遍历的顺序是:左、根、右。我们使用一个栈来保存节点,以便于迭代的时候取出对应节点。- 初始化的时候,遍历当前节点的左子树,将其路径上的节点存储到栈中。
- 调用
next方法的时候,从栈顶取出节点- 因为之前已经将路径上的左子树全部存入了栈中,所以此时该节点的左子树为空
- 取出该节点的右子树,再将右子树的左子树进行递归遍历,并将其路径上的节点存储到栈中。
- 调用
hasNext的方法的时候,直接判断栈中是否有值即可。
class BSTIterator:def __init__(self, root: TreeNode):self.stack = []self.in_order(root)def in_order(self, node):while node:self.stack.append(node)node = node.leftdef next(self) -> int:node = self.stack.pop()if node.right:self.in_order(node.right)return node.valdef hasNext(self) -> bool:return len(self.stack)
4.3 二叉搜索树中的搜索、插入和删除
- 0070 二叉搜索树中的搜索
- 0701 二叉搜索树中的插入操作
- 0450 删除二叉搜索树中的节点
4.3.1 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。找到值为val的节点并返回以这个节点为根的子树。 如果节点不存在,则返回 null 。
示例:
输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
class Solution(object):def searchBST(self, root, val):""":type root: TreeNode:type val: int:rtype: TreeNode"""if root:if val<root.val:return self.searchBST(root.left,val)elif val>root.val:return self.searchBST(root.right,val)else:return rootelse:return None
4.3.2 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。
- 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
- 可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
- 示例:
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]

结果也可以是:

解题思路:
在二叉搜索树中,对任意节点都有:root.left.val < root.val<root.right.val。所以需要根据 val 和当前节点的大小关系,来确定将 val 插入到当前节点的哪个子树上。
- 如果key比当前节点小,递归地放到其左子树,如果没有左子树,就直接作为其左子节点
- 如果key比当前节点大,递归地放到其右子树,如果没有右子树,就直接作为其右子节点
class Solution(object):def insertIntoBST(self, root, val):""":type root: TreeNode:type val: int:rtype: TreeNode"""if not root:root=TreeNode(val)return rootelse:if val>root.val:if root.right:self.insertIntoBST(root.right,val) else:root.right=TreeNode(val)else:if root.left:self.insertIntoBST(root.left,val)else:root.left=TreeNode(val)return root
或者是:
class Solution(object):def insertIntoBST(self, root, val):""":type root: TreeNode:type val: int:rtype: TreeNode"""if not root:root=TreeNode(val)return rootelse: # 如果val比root的值大,就递归其右子树。当当前节点没有右子节点时,插入到其右子节点if val>root.val: root.right=self.insertIntoBST(root.right,val) else:root.left=self.insertIntoBST(root.left,val)return root
4.3.3 删除二叉树中的节点
给定一个二叉搜索树的根节点 root,以及一个值 key。要求从二叉搜索树中删除 key 对应的节点。并保证删除后的树仍是二叉搜索树。
- 算法时间复杂度为 0(h)0(h)0(h),hhh 为树的高度。最后返回二叉搜索树的根节点。
- 示例;
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
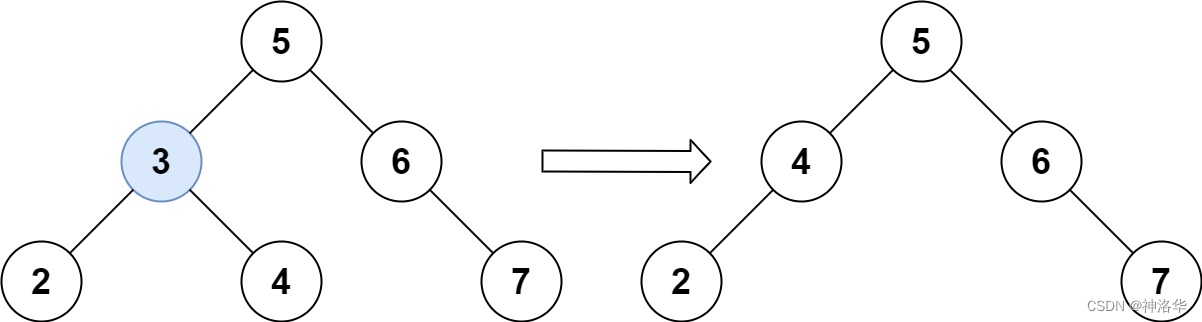
删除分两个步骤:查找和删除。查找通过递归查找,删除的话需要考虑情况。
- 从根节点
root开始,递归遍历搜索二叉树。 - 如果当前节点节点为空,返回当前节点。
- 如果当前节点值大于
key,则去左子树中搜索并删除,此时root.left也要跟着递归更新,递归完成后返回当前节点。 - 如果当前节点值小于
key,则去右子树中搜索并删除,此时root.right也要跟着递归更新,递归完成后返回当前节点。 - 如果当前节点值等于
key,则该节点就是待删除节点。- 如果当前节点的左子树为空,则使用其右子树代替当前节点位置,返回右子树。
- 如果当前节点的右子树为空,则使用其左子树代替当前节点位置,返回左子树。
- 如果当前节点的左右子树都有,则将左子树转移到右子树最左侧的叶子节点位置上,相当于被删节点没有了左子树,然后按照没有左子树处理。
class Solution(object):def deleteNode(self, root, key):""":type root: TreeNode:type key: int:rtype: TreeNode"""if not root:return rootelse:# 根据val的值进行递归地遍历,并更新root的左右子树if key>root.val: root.right=self.deleteNode(root.right,key)return root elif key<root.val:root.left=self.deleteNode(root.left,key)return rootelse: if not root.left: # 被删除节点的左子树为空。 return root.right # 令其右子树代替被删除节点的位置elif not root.right: # 被删除节点的右子树为空 return root.left # 令其左子树代替被删除节点的位置else:# 当被删节点有两个子节点的时候,找到被删节点的后继节点,即其右子树的最左侧cur=root.rightwhile cur.left:cur=cur.left# 将当前节点的左子树(root.Left)挂到其后继节点左侧,当前节点就没有左子树了cur.left=root.left return root.right # 使用其右子树代替当前节点位置
4.4 数据流中的第 K 大元素
0703. 数据流中的第 K 大元素
设计一个 KthLargest 类,用于找到数据流中第 k 大元素。
KthLargest(int k, int[] nums):使用整数 k 和整数流 nums 初始化对象。int add(int val):将 val 插入数据流 nums 后,返回当前数据流中第 k 大的元素。
输入:
["KthLargest", "add", "add", "add", "add", "add"]
[[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]
输出:
[null, 4, 5, 5, 8, 8]解释:
KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]);
kthLargest.add(3); // return 4
kthLargest.add(5); // return 5
kthLargest.add(10); // return 5
kthLargest.add(9); // return 8
kthLargest.add(4); // return 8
思路:使用最小堆保存前K个最大的元素,堆顶就是第k大的元素
- 建立大小为
k的最小堆,将前K个最大元素压入堆中。 - 每次
add操作时,将新元素压入堆中,如果堆中元素超出了k个,则将堆中最小元素(堆顶)移除,保证堆中元素保证不超过k个。 - 此时堆中最小元素(堆顶)就是整个数据流中的第
k大元素。
- 大顶堆:根节点值 ≥ 子节点值,也叫最大堆
max heap,最大key排在队首。- 小顶堆:根节点值 ≤ 子节点值,也叫最小堆
min heap,最小key排在队首
Python heapq库的用法介绍:
- heapq.heapify(list):从列表创建最小堆
- heapq._heapify_max(list):从列表创建最大堆
- heappush(heap, item):将数据item入堆
- heappop(heap):将堆中最小元素出堆(最小的就是堆顶)
- heapq.heapreplace(heap.item) :先操作heappop(heap),再操作heappush(heap,item)。
- heapq.heappushpop(list, item):先操作heappush(heap,item),再操作heappop(heap),和上一个函数相反。
- heapq.merge(*iterables):合并多个堆,例如
a = [2, 4, 6],b = [1, 3, 5],c = heapq.merge(a, b)- heapq.nlargest(n, iterable,[ key]):返回堆中的最大n个元素
- heapq.nsmallest(n, iterable,[ key]):返回堆中最小的n个元素
- heapq[0]:返回堆顶
示例:
array = [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21]
heapq.heapify(array)
print(heapq.nlargest(2, array))
print(heapq.nsmallest(3, array))[50, 45]
[5, 7, 10]
代码:
class KthLargest(object):import heapqdef __init__(self, k, nums):""":type k: int:type nums: List[int]"""self.k=kself.queue=nums heapq.heapify(self.queue)print(self.queue)def add(self, val):""":type val: int:rtype: int"""heapq.heappush(self.queue,val)while len(self.queue)>self.k:heapq.heappop(self.queue)return self.queue[0]
4.5 二叉搜索树的第k大节点
- 剑指 Offer 54 二叉搜索树的第k大节点
- 0230 二叉搜索树中第K小的元素
给定一棵二叉搜索树,请找出其中第 k 大的节点的值。
4.5.1 中序递归遍历
- 存储遍历结果,取第n-k个元素的值
class Solution(object):def __init__(self,ans=None):self.ans=[]def kthLargest(self, root, k):""":type root: TreeNode:type k: int:rtype: int"""ans=self.inorder(root)return ans[len(ans)-k]def inorder(self,root):# 中序遍历if root:self.inorder(root.left)self.ans.append(root.val)self.inorder(root.right) return self.ans
- 中序的倒序遍历,返回第k个结果
- 终止条件: 当节点 root 为空(越过叶节点),则直接返回;
- 递归右子树: 即 dfs(root.right) ;
- 提前返回: 若 k=0 ,代表已找到目标节点,无需继续遍历,因此直接返回;
- 统计序号: 执行 k=k−1
- k=0 ,代表当前节点为第 k 大的节点,因此记录 res=root.val ;
- 递归左子树: 即 dfs(root.left) ;
class Solution(object):def kthLargest(self, root, k):""":type root: TreeNode:type k: int:rtype: int"""self.k = kdef dfs(root):if not root: returndfs(root.right)self.k -= 1if self.k == 0: self.res = root.valreturndfs(root.left)dfs(root) return self.res
直接self.k == 0时,self.res存储结果,再return self.res,会返回空。
4.5.2 迭代
class Solution(object):def kthLargest(self, root, k):""":type root: TreeNode:type k: int:rtype: int"""stack=[]while stack or root:while root:stack.append(root)root=root.rightroot=stack.pop() # 二叉树最右下角即是最小的元素k-=1if k==0:return root.valroot=root.left
或者是:
class Solution(object):def kthLargest(self, root, k):""":type root: TreeNode:type k: int:rtype: int"""stack=[]while stack or root:if root:stack.append(root)root=root.rightelse:node=stack.pop()k-=1if k==0:return node.valroot=node.left
4.6 二叉搜索树的最近公共祖先
0235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树的根节点 root,以及其中两个指定节点 p 和 q,找到该这两个指定节点的最近公共祖先。
说明:
- 祖先:若节点
p在节点node的左子树或右子树中,或者p == node,则称node是p的祖先。 - 最近公共祖先:对于树的两个节点
p、q,最近公共祖先表示为一个节点lca_node,满足lca_node是p、q的祖先且lca_node的深度尽可能大(一个节点也可以是自己的祖先)。 - 所有节点的值都是唯一的。
p、q为不同节点且均存在于给定的二叉搜索树中。- 示例:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。如果是节点 2 和节点 4 ,其最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

对于节点 p、节点 q,最近公共祖先就是从根节点分别到它们路径上的分岔点,也是路径中最后一个相同的节点,现在我们的问题就是求这个分岔点。
我们可以使用递归遍历查找二叉搜索树的最近公共祖先,具体方法如下。
- 从根节点
root开始遍历。 - 如果当前节点的值大于
p、q的值,说明p和q应该在当前节点的左子树,因此将当前节点移动到它的左子节点,继续遍历; - 如果当前节点的值小于
p、q的值,说明p和q应该在当前节点的右子树,因此将当前节点移动到它的右子节点,继续遍历; - 如果当前节点不满足上面两种情况,则说明
p和q分别在当前节点的左右子树上,则当前节点就是分岔点,直接返回该节点即可。
class Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':ancestor = rootwhile True:if ancestor.val > p.val and ancestor.val > q.val:ancestor = ancestor.leftelif ancestor.val < p.val and ancestor.val < q.val:ancestor = ancestor.rightelse:breakreturn ancestor
4.7 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
- 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
- 示例:
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:

思路 1:递归遍历
直观上,如果把数组的中间元素当做根,那么数组左侧元素都小于根节点,右侧元素都大于根节点,且左右两侧元素个数相同,或最多相差 111 个。那么构建的树高度差也不会超过 111。
所以猜想出:如果左右子树越平均,树就越平衡。这样我们就可以每次取中间元素作为当前的根节点,两侧的元素作为左右子树递归建树,左侧区间 [L,mid−1][L, mid - 1][L,mid−1] 作为左子树,右侧区间 [mid+1,R][mid + 1, R][mid+1,R] 作为右子树。
class Solution:def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:def build(left, right):if left > right:return mid = left + (right - left) // 2root = TreeNode(nums[mid])root.left = build(left, mid - 1)root.right = build(mid + 1, right)return rootreturn build(0, len(nums) - 1)
4.8 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
高度平衡二叉树:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1
思路:递归遍历
- 先递归遍历左右子树,判断左右子树是否平衡,再判断以当前节点为根节点的左右子树是否平衡。
- 如果遍历的子树是平衡的,则返回它的高度,否则返回 -1。
- 只要出现不平衡的子树,则该二叉树一定不是平衡二叉树。
class Solution:def isBalanced(self, root: TreeNode) -> bool:def height(root: TreeNode) -> int:if not root:return 0leftHeight = height(root.left)rightHeight = height(root.right)if leftHeight == -1 or rightHeight == -1 or abs(leftHeight - rightHeight) > 1:return -1else:return max(leftHeight, rightHeight) + 1return height(root) >= 0
