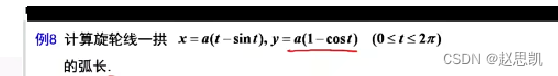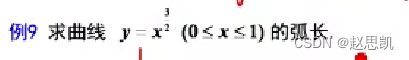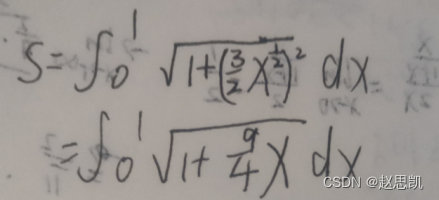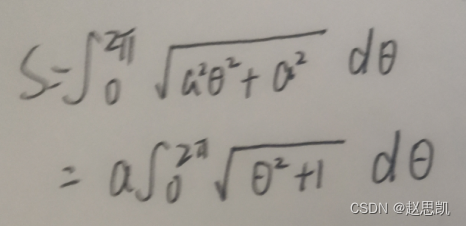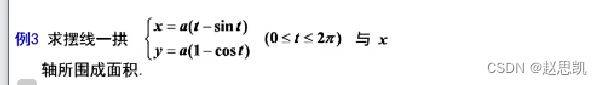定积分在几何上的应用

定积分的元素法

目录

定积分的元素法

 平面图形的面积问题：

 ​编辑

 极坐标方程

 例题：

旋转体的体积：

 平面曲线的弧长：

 弧长的三个公式：

 例题：

 例如：

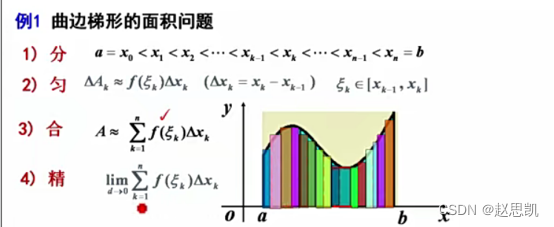
 步骤1：我们先把区间a,b分成n个区间

步骤2：我们在一个区间中设置一点ξ点，用这一点的函数值代替区间内部所有的函数值，让函数值×这一点的区间长度

步骤3：我们把这n个区间的面积全部加起来表示曲边梯形面积的近似值。

步骤4：我们求出当d趋近于0时，面积的近似值的极限，d表示区间长度的最大值，当最大值趋近于0时，表示近似值无限接近于真实值。

这个极限就是我们求的曲边梯形面积的准确值。

我们如何求一个区间的面积呢？

如图：

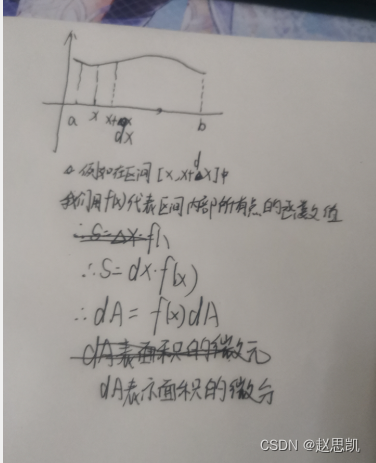
这种方法就叫做定积分的元素法。

 平面图形的面积问题：

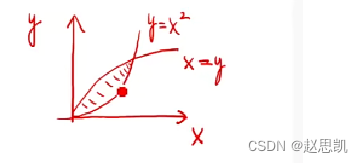
 如图所示，我们要求阴影部分的面积

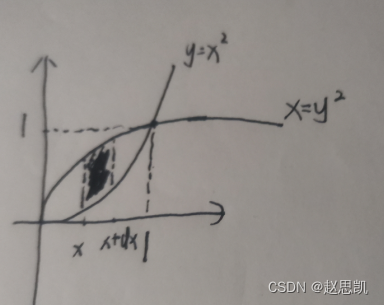
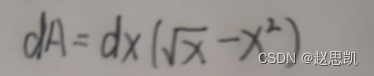
 我们进行求解：

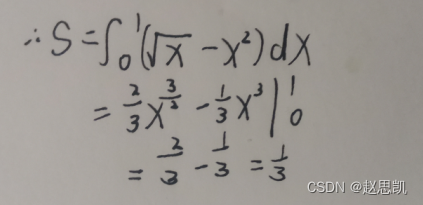
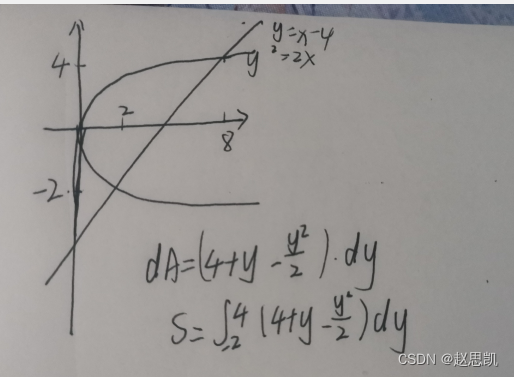
 我们也可以尝试在y轴进行积分：

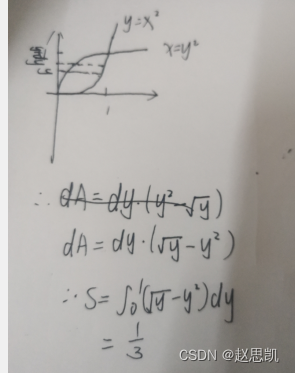
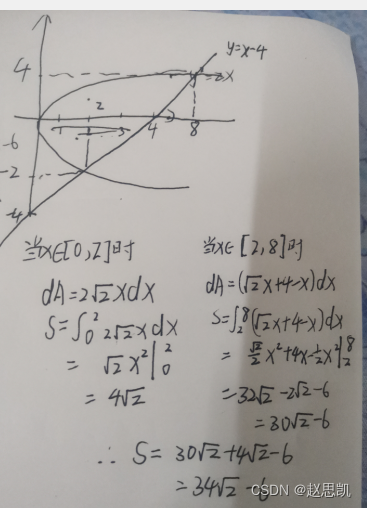
在y轴进行积分时：

 极坐标方程

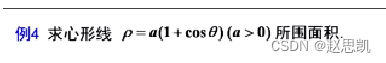
 我们先引出极坐标方程的一般规律

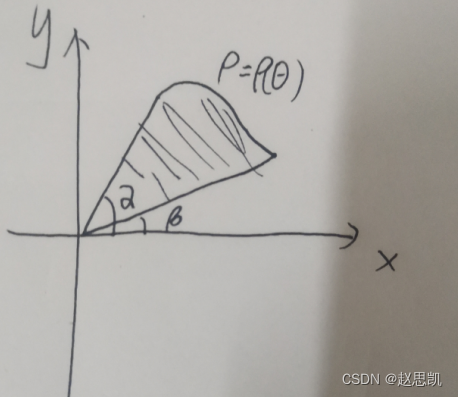
我们如何求围成图形的面积呢？

 所以极坐标围成图形的面积公式：

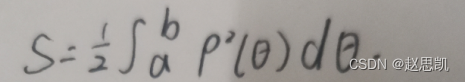
 例题：

旋转体的体积：

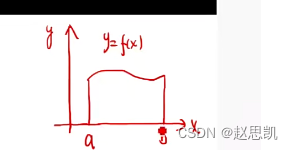
 例如：求如图所示的曲边梯形绕x轴旋转一周形成的旋转体的体积

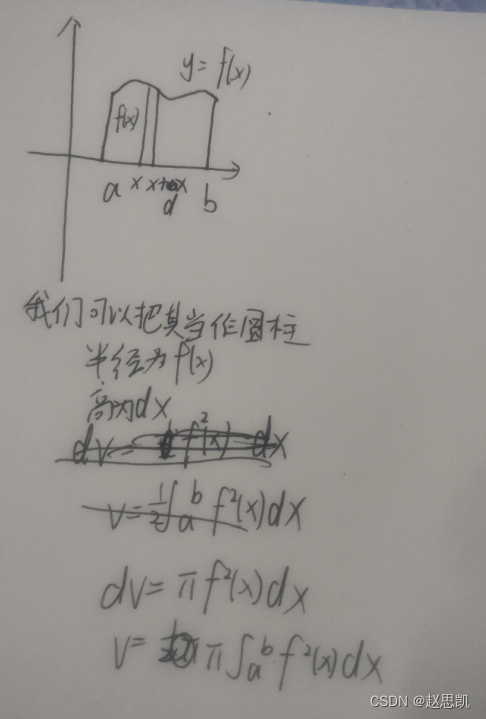
 所以绕x轴旋转的体积公式是：

 假如我们要把这个图像绕y轴进行旋转呢？

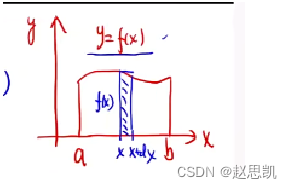
 我们转出的就是一个圆筒，我们要求圆筒的体积可以把圆筒展开成为一个长方体。

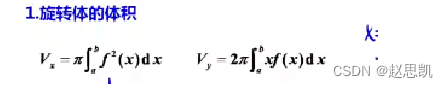
 我们直接带入公式：

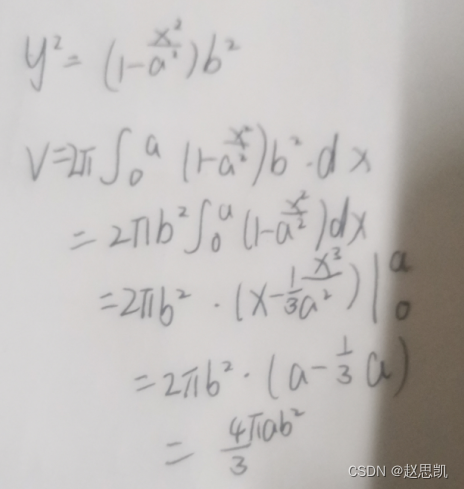
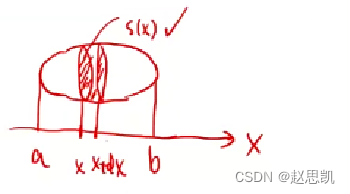
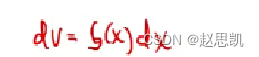
 所以平行截面积为已知的立体的体积公式为

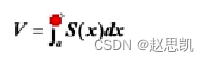
 对于旋转体绕x轴y轴形成的体积问题，也可以使用这种方法解决：

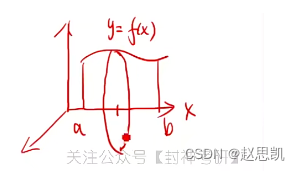
 例如该图像绕x轴旋转形成的面积。

截面的面积是一个圆。

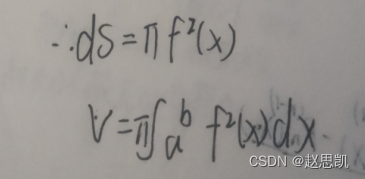
 平面曲线的弧长：

 我们首先把弧分成n个小区间，在这n个小区间中，用直线来代替曲线。

然后把这些曲线加起来求出来的就是弧长的近似值，我们再使用极限，入代表的含义是这n个区间中长度的最大值，当最大值都趋近于0，这个过程代表无限，通过无限过程把曲线的问题转换为直线。

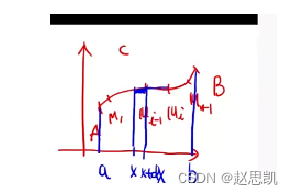
 我们要注意，dx在这里并不能够代表曲线，我们可以 通过三角函数更具体的表示出曲线的长度。

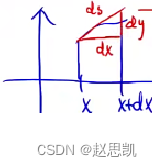
再进行积分，所以我们要求作的弧长公式为：

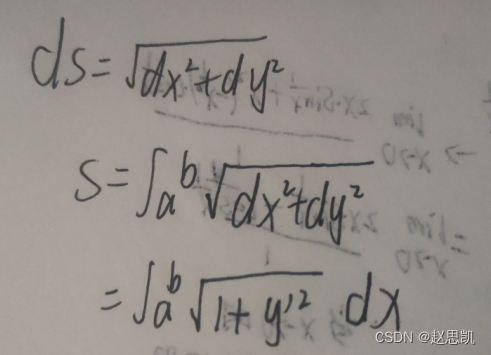
 弧长的三个公式：

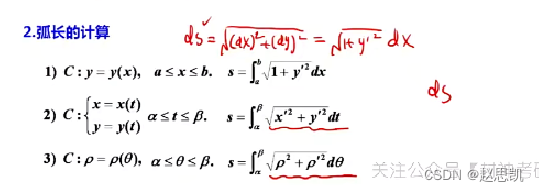
 例题：