一，定义

kruskal是求最小生成树的一种算法。最小生成树

但是这种结合并查集的特殊方法给了他许多特殊的性质。可以用于解决树上瓶颈边权之类的问题

结合这种算法而诞生的就是——kruskal重构树

二，建树思路及其性质

kruskal求最小生成树是将边权小的边先连起来。而重构树则是同理，他把当前最小边抽象为一个虚点（虚点的值为该边权值），然后把这条边对应的两个不同集合视为左右儿子，将集合与该虚点建边

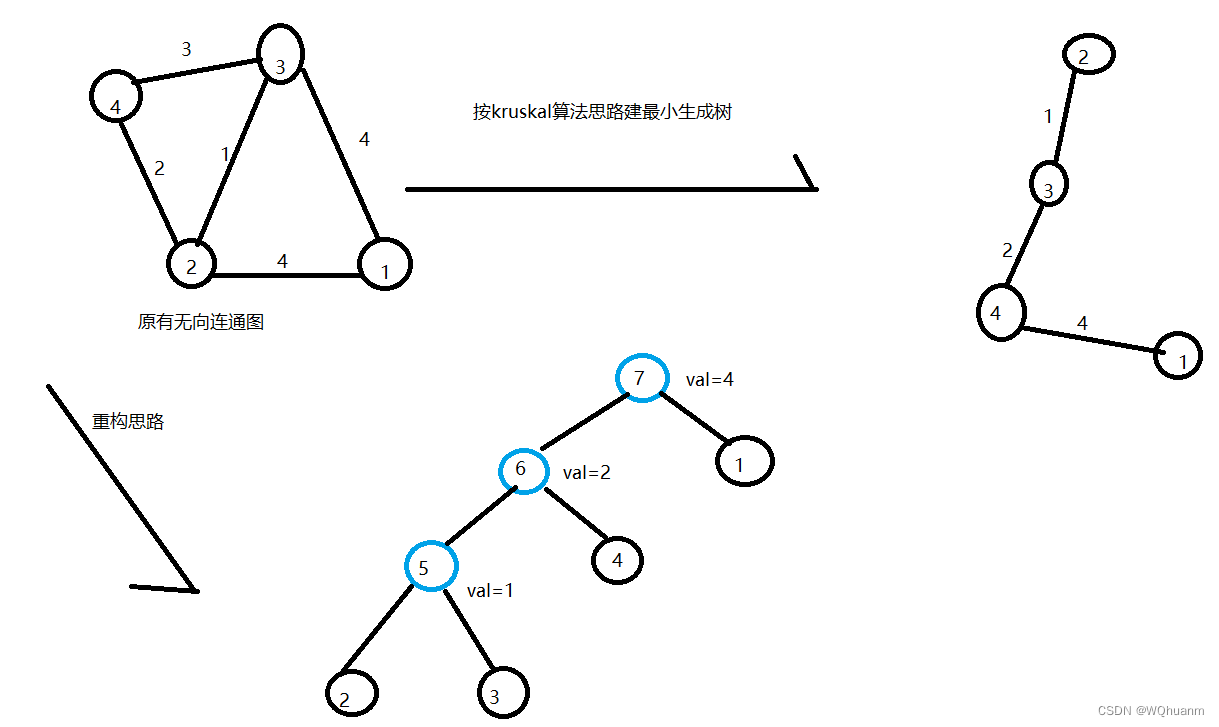
 建树后我们很清晰地发现它有如下性质

1. 是一颗二叉树
2. 虚点有n-1个，且值随着树的建立不断变大（因为是从小边建到大边嘛）
3. 父节点都是虚点，叶子节点都是原来图中的点
4. 如果我们从图中任意x点到y点，那么他们路过的最大边权边就是他们的重构树lca虚点val值
5. 换句话说：原图中x到y的所有简单路径中最大边权的最小值是val[lca(x,y)](因为所有路径中，每条边都最小的肯定是最小生成树的，那么最小中的最大边权也肯定是所有路径中最大边权中最小的）==最小生成树上两个点之间的简单路径上的最大值= Kruskal 重构树上两点之间的 LCA 的权值

例题一：P1967 [NOIP2013 提高组] 货车运输 

思路：如果我们建最大生成树，那么lca(x,y)就是所有路径能通过的最小边权的最大值

#include <bits/stdc++.h>
using namespace std;
#define ll               long long
#define endl             "\\n"
#define int              long long
#define endll            endl<<endl
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<long long, long long> pll;
//---------------------------------------------------------------------------------------------------------------------//
//---------------------------------------------------------------------------------------------------------------------//
//double 型memset最大127，最小128
const int INF = 0x3f3f3f3f;         //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int N = 2e5 + 10;
struct node
{int u,v,w;bool operator<(const node&k)const{return w>k.w;}
} b[N<<1];
vector<int>edge[N<<1];
int fa[N],val[N<<1],dep[N],pre[N][32];int find(int x)//并查集
{if(fa[x]!=x)fa[x]=find(fa[x]);return fa[x];
}void dfs(int u,int f)//遍历重构树建立深度与预处理lca
{dep[u]=dep[f]+1;pre[u][0]=f;for(int i=1; i<=20; ++i)pre[u][i]=pre[pre[u][i-1]][i-1];for(auto v:edge[u])if(v!=f)dfs(v,u);
}int LCA(int u,int v)
{if(dep[u]<dep[v])swap(u,v);if(dep[u]>dep[v]){int k=log2(dep[u]-dep[v]);for(int i=k; i>=0; --i)if(dep[pre[u][i]]>=dep[v])u=pre[u][i];}if(u==v)return u;int k=log2(dep[u]);for(int i=k; i>=0; --i)if(pre[u][i]!=pre[v][i])u=pre[u][i],v=pre[v][i];return pre[u][0];
}void mysolve()
{int n,m;cin>>n>>m;for(int i=1; i<=2*n; ++i)fa[i]=i;for(int i=1; i<=m; ++i)cin>>b[i].u>>b[i].v>>b[i].w;sort(b+1,b+1+m);int cnt=n;for(int i=1; i<=m; ++i)//重构{int fu=find(b[i].u),fv=find(b[i].v);if(fu!=fv){val[++cnt]=b[i].w;fa[fu]=fa[fv]=cnt;edge[cnt].push_back(fu),edge[cnt].push_back(fv);}}for(int i=cnt; i>n; --i)if(fa[i]==i)dfs(i,i);//可能是森林int q,x,y;cin>>q;while(q--){cin>>x>>y;if(find(x)!=find(y))cout<<-1<<endl;else cout<<val[LCA(x,y)]<<endl;}}
int32_t main()
{std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll t=1;//cin >> t;while (t--){mysolve();}system("pause");return 0;
}

例题二：P4768 [NOI2018] 归程 

思路：

1. 首先，我们容易想到，每次询问，只需要开车开到能靠近家（1点）位置，剩下走路即可
2. 我们询问可以有logq的复杂度
3. 那么我们如果先用dijksta预处理每个点到家的最短距离，然后我们重构树不是每个虚点子代的点表示只要你这个虚点我能来（我们建最大生成树），那么你的子节点我就能到达，所以这个虚点可以存储子树集合到达家的最小值。
4. 那么我们每次 每次询问v点，尽可能跳到最大的祖先，剩下不行距离就是该祖先点存储的子树中到达家的最小距离。（能通过虚点说明子树是可以任意通过的）

#include <bits/stdc++.h>
using namespace std;
#define ll               long long
#define endl             "\\n"
typedef pair<int, int> pii;
const int INF = 0x3f3f3f3f;         //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int N = 1e6 + 10;struct node//kruskal的海拔
{int u,v,w;bool operator<(const node&k)const{return w>k.w;}
} b[N];struct node1//最短路
{int next,to,w;
} edge[N];
int fa[N],pre[N][32],val[N],dis[N],head[N],num,cnt;
int dep[N];
vector<int>eg[N];//重构树的边void add(int u,int v,int w)
{edge[++num].next=head[u];edge[num].to=v;edge[num].w=w;head[u]=num;
}void init(int n)
{for(int i=1; i<=2*n; ++i)fa[i]=i,fa[n+i]=n+i,eg[i].clear(),head[i]=0;//注意，重构树建立后点变成两遍，所以开空间要开两倍，初始化也要num=0,cnt=n;
}int find(int x)
{if(fa[x]!=x)fa[x]=find(fa[x]);return fa[x];
}void dijkstra(int n)
{for(int i=1; i<=2*n; ++i)dis[i]=INF;//2n个点，包含虚点，跑dij不会碰到虚点（都没出生呢），一开始虚点显然离终点无限远dis[1]=0;priority_queue<pii,vector<pii>,greater<pii>>q;q.push({dis[1],1});while(!q.empty()){int u=q.top().second;q.pop();for(int i=head[u]; i; i=edge[i].next){int v=edge[i].to,w=edge[i].w;if(dis[v]>dis[u]+w){dis[v]=dis[u]+w;q.push({dis[v],v});}}}
}void kruskal(int n,int m)
{sort(b+1,b+1+m);cnt=n;for(int i=1; i<=m; ++i){int fu=find(b[i].u),fv=find(b[i].v);if(fu!=fv){val[++cnt]=b[i].w;fa[fu]=fa[fv]=cnt;eg[cnt].push_back(fu),eg[cnt].push_back(fv);}}
}void dfs(int u,int f)
{dep[u]=dep[f]+1;pre[u][0]=f;for(int i=1; i<=20; ++i)pre[u][i]=pre[pre[u][i-1]][i-1];for(auto v:eg[u])if(v!=f){dfs(v,u);dis[u]=min(dis[v],dis[u]);//存储虚点的子树的最小距离}
}void mysolve()
{int n,m;cin>>n>>m;init(n);int x,y,d,w;for(int i=1; i<=m; ++i){cin>>x>>y>>d>>w;add(x,y,d),add(y,x,d);b[i].u=x,b[i].v=y,b[i].w=w;}dijkstra(n);kruskal(n,m);dfs(cnt,0);int q,k,s;cin>>q>>k>>s;int v,p,lantans=0;while(q--){cin>>v>>p;v=(v+k*lantans-1)%n+1;p=(p+k*lantans)%(s+1);int h=log2(dep[v]);for(int i=h; i>=0; --i)if(dep[pre[v][i]]&&val[pre[v][i]]>p)v=pre[v][i];cout<<(lantans=dis[v])<<endl;}
}int32_t main()
{std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll t=1;cin >> t;while (t--){mysolve();}system("pause");return 0;
}