数学前置

Jacobian矩阵：给定函数 f:Rn×Rmf: \\R^{n}\\times \\R^mf:Rn×Rm，该函数的所有一阶偏导数组成的矩阵 $J$ 称为 Jacobian 矩阵
J=[∂f1∂x1...∂f1∂xn.........∂fm∂x1...∂fm∂xn]m×nJ = \\begin{bmatrix} \\frac{\\partial f_1}{\\partial x_1} & ... & \\frac{\\partial f_1}{\\partial x_n}\\\\ ... & ... & ...\\\\ \\frac{\\partial f_m}{\\partial x_1} & ... & \\frac{\\partial f_m}{\\partial x_n} \\end{bmatrix}_{m\\times n} J=​∂x1​∂f1​​...∂x1​∂fm​​​.........​∂xn​∂f1​​...∂xn​∂fm​​​​m×n​
若 $m=n$，可以定义关于方阵 $J$ 的行列式
det(J)=∑j1,...,jn(−1)τ(j1...jn)a1,j1...an,jn\\text{det}(J) = \\sum_{j_1,...,j_n}(-1)^{\\tau(j_1...j_n)} a_{1,j_1}...a_{n,j_n} det(J)=j1​,...,jn​∑​(−1)τ(j1​...jn​)a1,j1​​...an,jn​​
其中 j1...jnj_1...j_nj1​...jn​ 是 $\mathrm{1...}n$ 的一个排列，$\tau (\cdot )$ 表示置换中逆序对的个数/从初始排列$(1,...,n)$交换得到该排列的次数，从含义角度来讲，行列式可以看作是有向面积/体积向 $n$ 维空间的一个推广，例如对于 $n=2$ 时，行列式的绝对值即为向量 (a1,1,a1,2)(a_{1,1},a_{1,2})(a1,1​,a1,2​) 与向量 (a2,1,a2,2)(a_{2,1}, a_{2,2})(a2,1​,a2,2​) 张成的平行四边形的面积

变量变换定理：给定随机变量 $z$ 及其概率密度函数 $\pi (z)$，对于新变量 $x$，若存在双射函数 $f$，满足 $x=f(z)$ 且 z=f−1(x)z=f^{-1}(x)z=f−1(x)，那么对于新变量 $x$ 的概率密度函数 $p(x)$，由于 ∫z∈Rπ(z)dz=∫x∈Rp(x)dx=1\\int_{z\\in \\R} \\pi(z) dz = \\int_{x\\in \\R} p(x) dx = 1∫z∈R​π(z)dz=∫x∈R​p(x)dx=1，有如下性质
p(x)∣dx∣=π(z)∣dz∣p(x)=π(z)∣dz∣∣dx∣=π(f−1(x))∣df−1dx∣p(x)|dx| = \\pi(z)|dz| \\\\ p(x) = \\pi(z)\\frac{|dz|}{|dx|} = \\pi(f^{-1}(x)) \\left|\\frac{d f^{-1}}{dx}\\right| p(x)∣dx∣=π(z)∣dz∣p(x)=π(z)∣dx∣∣dz∣​=π(f−1(x))​dxdf−1​​
扩展到向量上，对于 f:Rn→Rnf:\\R^n\\rightarrow \\R^nf:Rn→Rn，有
p(x)=π(f−1(x))∣det(Jf−1)∣p(x) = \\pi(f^{-1}(x))|\\text{det}(J_{f^{-1}})| p(x)=π(f−1(x))∣det(Jf−1​)∣

Flow-based Model

假定真实数据分布 $q$，数据集中每个数据点 xix_ixi​ 可以看作是一个采样 $x\sim q(x)$，我们希望使用模型 fθ(⋅)f_{\\theta}(\\cdot)fθ​(⋅) 建模真实数据分布 $q$，使得对于已知分布 $z\sim \pi (z)$，可以通过 fθ(z)f_\\theta(z)fθ​(z) 将其变换到拟合出的真实数据分布 pθp_\\thetapθ​ 上，训练目标即为最小化KL散度 KL(q(x)∣∣pθ(x))\\text{KL}(q(x)||p_{\\theta(x)})KL(q(x)∣∣pθ(x)​)，等价于最大化对数似然函数
arg⁡max⁡θ∑i=1Nlog⁡pθ(x(i))\\arg \\max_\\theta \\sum_{i=1}^N \\log p_\\theta(x^{(i)}) argθmax​i=1∑N​logpθ​(x(i))
其中 x(i)x^{(i)}x(i) 为从真实数据分布 $q$ 中的 $N$ 次采样，利用变量变换定理，可得
log⁡pθ(x(i))=log⁡π(f(−1)(x(i)))+log⁡∣det(Jf−1)∣\\log p_\\theta(x^{(i)}) = \\log \\pi(f^{(-1)}(x^{(i)}))+\\log |\\text{det}(J_{f^{-1}})| logpθ​(x(i))=logπ(f(−1)(x(i)))+log∣det(Jf−1​)∣
在训练过程中，我们只需要利用 f(−1)f^{(-1)}f(−1)，而在推理过程中，我们使用 $f$ 进行生成，因此对 $f$ 约束为：$f$ 网络是可逆的。这对网络结构要求比较严格，在实现时，通常要求 $f$ 的输入输出是相同维度的来保证 $f$ 的可逆性。注意到，如果 $f$ 可以表示为若干映射的叠加 f=f1∘f2∘...fKf = f_1\\circ f_2\\circ ... f_Kf=f1​∘f2​∘...fK​，那么有
log⁡pθ(x(i))=log⁡π(f(−1)(x(i)))+∑k=1Klog⁡∣det(Jfk−1)∣\\log p_\\theta(x^{(i)}) = \\log \\pi(f^{(-1)}(x^{(i)}))+\\sum_{k=1}^{K}\\log |\\text{det}(J_{f_k^{-1}})| logpθ​(x(i))=logπ(f(−1)(x(i)))+k=1∑K​log∣det(Jfk−1​​)∣

RealNVP

整体思路是，固定特征的一部分，利用该部分预测一个针对其他部分的仿射变换的参数，这里 $s(\cdot ),t(\cdot )$ 两部分没有约束，这是因为

在计算行列式的时候，由于空子矩阵的存在，因此 $s,t$ 并不影响最终的行列式的值。堆叠该变换时，可以交替设置恒等映射的特征维度，以此来建模全体维度的变换

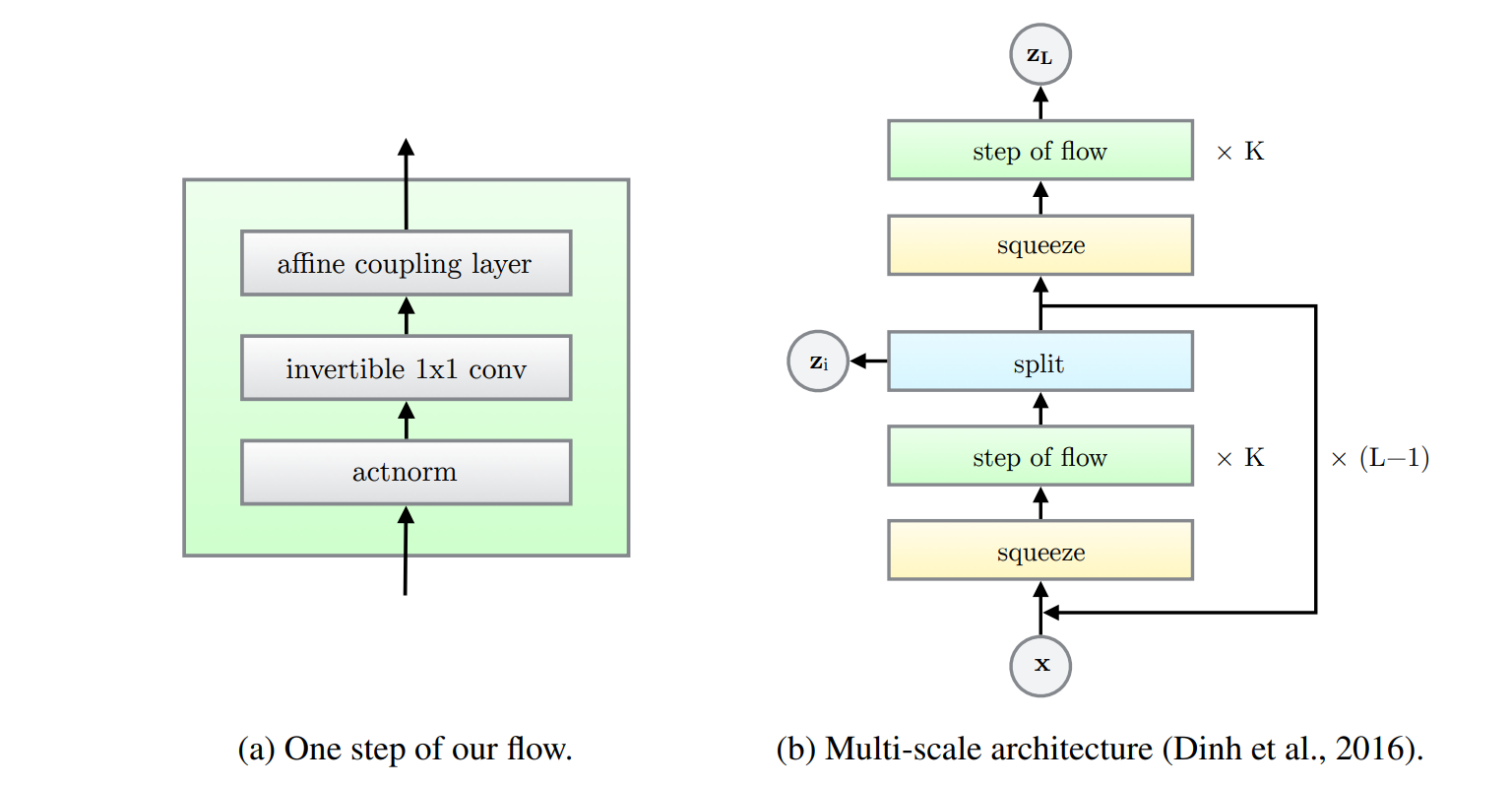
GLOW

GLOW对RealNVP进行进一步的扩展，使用可逆的$1\times 1$的卷积来建模跨通道的特征依赖，避免对通道进行重排，简化架构

参考资料

DENSITY ESTIMATION USING REAL NVP
Glow: Generative Flow with Invertible 1×1 Convolutions
Flow-based Deep Generative Models
Flow-based Generative Model