【C++】map与set容器——红黑树底层封装

目录
- 前言
- 1. set
-
- 1.1 set的概念
- 1.2 set的使用
- 2. map
-
- 2.1 map的概念
- 2.2 map的使用
- 3. multiset和multimap
- 4. 红黑树模拟实现map和set
-
- 4.1 改造红黑树
- 4.2 红黑树的迭代器
-
- 4.2.1 STL中的rb_tree结构与其迭代器设计
- 4.2.2 模拟实现红黑树的迭代器
- 4.3 map和set的迭代器
- 4.4 map和set的插入操作
- 4.5 map和set最终实现
前言
💭STL中,容器大概可分为两种类型——序列式容器和关联式容器。在前面的系列文章中,我们已经介绍了诸多序列式容器,如:vector、list、stack、queue等,它们以序列的形式存储数据。
💭而关联式容器也是一种非常重要的容器。标准的STL关联式容器分为set(集合)和map(映射表)两大类,以及这两大类的衍生体multiset和multimap。这些容器的底层机制均以RBTree实现,也就是上文我们所说的红黑树,这正是本文的重点所在。怎么用红黑树实现map和set?为什么?本文将解决这一系列问题。
🔎下面是关联式容器 (associative containers) 的概念
所谓关联式容器,观念上类似关联式数据库(实际上则简单许多):每笔数据(每个元素),都有一个键值(key)和一个实值(valve),当元素被插入到关联式容器中时,容器内部结构(可能是 RB-tree,也可能是 hash-table)便依照其键值大小,以某种特定规则将这个元素放置于适当位置。关联式容器没有所谓头尾(只有最大元素和最小元素),所以不会有所谓 push_ back()、push_ front()、pop_back()、pop_front()这样的操作行为。
节选自《STL源码剖析》一书
1. set
1.1 set的概念
📝 set是一种关联式容器,其特性如下:
- set的所有元素都会根据元素的键值被自动排列
- set的底层是红黑树
- set不像map同时拥有键值(key)和实值(value),set的键值就是实值
- set不允许两个元素有相同的键值,即每个键值都是唯一的
- set的元素不能在容器中修改,但是可以插入或删除。
🔎为什么set的元素不能在容器中修改?
因为set元素值就是其键值,其关系到set元素的排列规则,一旦任意修改了set元素值,会严重破坏set的组织结构。
1.2 set的使用
包含头文件:#include <set>
1️⃣set的模板参数
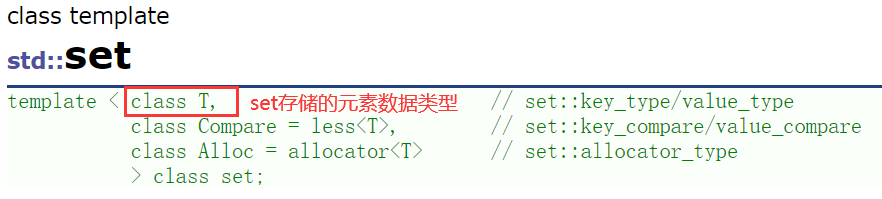
- T:set中存放元素的类型,实际在底层存储<value, value>的键值对。
- Compare:set的元素排序比较方式,默认按照小于来比较。
- Alloc:set中元素空间的管理方式,使用STL提供的空间配置器管理。
2️⃣set的接口使用
💭set的构造函数有三种,主要的接口有insert、find、erase,比较简单,此处不再展开介绍。
| 构造函数功能 | 接口 |
|---|---|
| 默认构造(构造一个空set) | set (const key_compare& comp = key_compare(),const allocator_type& alloc = allocator_type()); |
| 迭代器区间构造(按两个迭代器指向的一系列元素构造set) | set (InputIterator first, InputIterator last) |
| 拷贝构造 | set (const set& x); |
📃set的文档介绍
💡基于set的特性,可以用于对一个序列进行
去重+排序的操作。
⭕下面是一段set的测试代码
void test_set()
{set<int> s;// set插入数据s.insert(7);s.insert(8);s.insert(6);s.insert(5);// set的迭代器支持了范围forfor (auto& k : s){cout << k << " ";}cout << endl;int a[] = { 1, 3, 5, 7, 9, 2, 4, 6, 8, 0, 1, 3, 5, 7, 9, 2, 4, 6, 8, 0 };// 迭代器范围,构造setset<int> ss(a, a + sizeof(a) / sizeof(a[0]));// set的迭代器支持了范围forfor (auto& k : ss){cout << k << " ";}
}
⭕运行结果,可见set确实可以达到去重+排序的目的
5 6 7 8
0 1 2 3 4 5 6 7 8 9
2. map
2.1 map的概念
📝map是一种关联式容器,其特性如下:
- map它按照特定的次序(按照key来比较)存储由键值key和值value组合而成的元素。
- 在map中,键值key通常用于排序和惟一地标识元素,而值value中存储与此键值key关联的内容。键值key和值value的类型可能不同,并且在map的内部,key与value通过成员类型value_type绑定在一起,为其取别名称为pair:
typedef pair<const key, T> value_type; - 在内部,map中的元素总是按照键值key进行比较排序的。
- map支持下标访问符,即在
[]中放入key,就可以找到与key对应的value。 - map的底层是红黑树
map支持下标访问符
[],体现了其映射的特点,即一个key值映射一个value,二者紧密关联。
2.2 map的使用
包含头文件:#include <map>
1️⃣map的模板参数
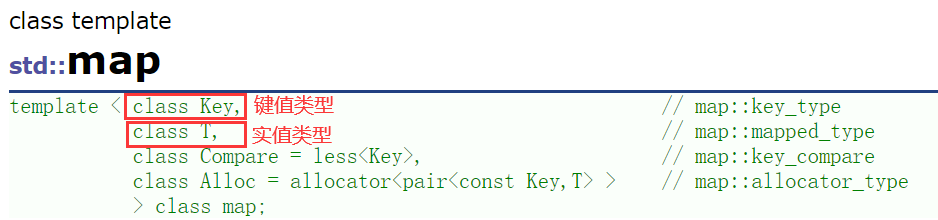
2️⃣map的接口使用
📃map的文档介绍
map的其他接口与set类似,不再过多介绍,此处重点介绍 map::operator[],即它的下标访问符重载函数。
map::operator[]不仅能够找到key对应的value,还有插入的功能,因此平时在使用map容器时,会频繁用到它。
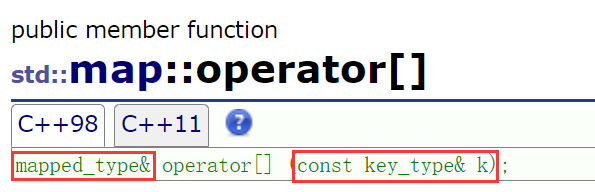
观察operator[]的接口可以看到,参数是一个键值,返回值是键值对应的实值(后面统称为value值)。
- 若map容器中键值为k的元素已经存在,则插入元素不会发生,直接返回键值k对应的value值。
- 若map容器中键值为k的元素不存在时,则会发生一个插入,插入一个键值为k的元素,对应value值为默认值(即value类型调用默认构造)。
A call to this function is equivalent to(该函数调用等价于):
(*((this->insert(make_pair(k,mapped_type()))).first)).second
🔎为了解operator[]的详细实现机制,还需了解map::insert()的实现
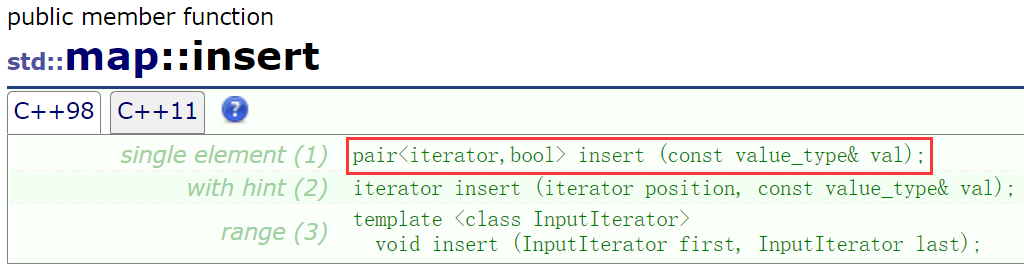
可见 operator[]调用了insert的单元素插入版本。
🔎map::insert()的机制是,向map容器插入一个元素:
- 若该元素已经存在(键值相同),则插入失败,并返回一个pair,
pair.first是指向已存在元素结点的迭代器,pair.second是false; - 若该元素不存在,则进行插入操作,并返回一个pair,
pair.first是指向新元素结点的迭代器,pair.second是true;
💭由此便可以解释
operator[]的实现机制,它调用insert,利用insert的返回值,取得键值对应元素节点的迭代器,再通过迭代器取得键值对应的value值,达成了通过key映射value的目的。
⭕map的插入通常有三种写法
void test_map()
{map<int, int> m;// 1.构造pair的匿名对象传给m.insert()m.insert(pair<int, int>(1, 1));m.insert(pair<int, int>(2, 2));// 2.利用make_pair函数构造键值对m.insert(make_pair(3, 3));m.insert(make_pair(4, 4));// 3.方括号(比较简洁)m[5] = 5;m[6] = 6;
}
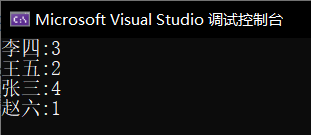
⭕利用map可以做一些统计工作,例如:统计人名出现的次数
void toCountName()
{string names[] = { "张三","张三","李四","王五","李四","王五" ,"张三" ,"张三" ,"李四" ,"赵六" };// 键值为人名, value值为人名出现次数map<string, int> countName;for (auto& name : names){// 人名存在,次数加1;人名不存在,先插入再次数加1countName[name]++;}// 输出人名及其出现次数for (auto& kv : countName){cout << kv.first << ":" << kv.second << endl;}
}
3. multiset和multimap
🔎multiset和set大致相同,唯一的不同点就是multiset中的键值允许相同,即其元素是可以重复的。
void test_multiset()
{int a[] = { 1, 3, 5, 7, 9, 2, 4, 6, 8, 0, 1, 3, 5, 7, 9, 2, 4, 6, 8, 0 };// 迭代器范围,构造multisetmultiset<int> ms(a, a + sizeof(a) / sizeof(a[0]));for (auto k : ms){cout << k << " ";}
}
⭕运行结果,可发现有相同的元素,可见multiset的作用之一是对序列排序而不去重
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
🔎同理,multimap和map也大致相同,唯一的不同点就是multimap中的键值允许重复。
而在STL标准库中,multimap中并没有重载operator[]操作,因为multimap一个键值key可能对应多个value值,无法达成一对一映射的效果,因此重载operator[]并无意义。
💭至于相同的元素节点应该如何插入,STL标准库源代码规定,multiset和multimap插入时使用rb_tree的insert_equal()函数,其中相同元素的节点插到它的右边。但其实插左插右并没有区别,经过旋转后结构相同。
4. 红黑树模拟实现map和set
💭重点来了!!STL已经帮我们造好了map和set两个轮子,而我们学习模拟实现不是为了造出更好的轮子,而是学会更好的使用轮子,熟悉其底层实现。
由于map和set所开放的各种操作接口,红黑树也都提供了,所以它们的操作都只是转调用了红黑树的操作行为而已,在红黑树的接口上略作修改,突出其二者各自的特性。
4.1 改造红黑树
💬RBTree的模板参数应该改成如下这样,才能适应map和set的配接。
//RBTree的节点
template <class V>
struct RBTreeNode
{typedef RBTreeNode<V> Self;V _v;// 数据域Self* _left;Self* _right;Self* _parent;COLOR _col;RBTreeNode(const V& v):_v(v), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}
};//RBTree
template <class K, class V, class KeyOfValue>
class RBTree
{typedef RBTreeNode<V> node;
public://...
private:node* _root;
}
- K:key,键值类型
- V:value,实值类型。若是map,则为pair<k,v>;若是set,则为k。
- KeyOfValue:仿函数,用于取出存储在value中的key值。因为map和set有不同的取key方式,所以需要有这样一个仿函数。
⭕map和set的大致框架:
// set
template <class K>
class set
{// set的KeyofValue仿函数,取key == 取valuestruct setKov{const K& operator()(const K& v){return v;}};public://...private:// 对于set来说,键值类型等同于数据类型// 故键值类型为K,实值类型也为KRBTree<K, K, setKov> _t;
};
// map
template <class K, class V>
class map
{// map的KeyofValue仿函数,value是一个键值对,取key == 取value的firststruct mapKov{const K& operator()(const pair<const K, V>& kv){return kv.first;}};public://...private:// 键值类型为K,实值类型为pair<const K, V>(key值不可修改)RBTree<K, pair<const K, V>, mapKov> _t;
};
4.2 红黑树的迭代器
4.2.1 STL中的rb_tree结构与其迭代器设计
💭迭代器是STL六大组件之一,对于容器的实现非常重要。因此,想要用红黑树封装map和set,红黑树必须提供迭代器。下面来看如何设计红黑树的迭代器(iterator)
红黑树是关联式容器,并没有所谓的头或尾,只有最大元素节点和最小元素节点(以键值大小为准),因此红黑树不能像vector、list一样将begin迭代器定义在序列头,end在序列尾。那么它的结构是如何设计的?我们先来看看标准库的实现方法。
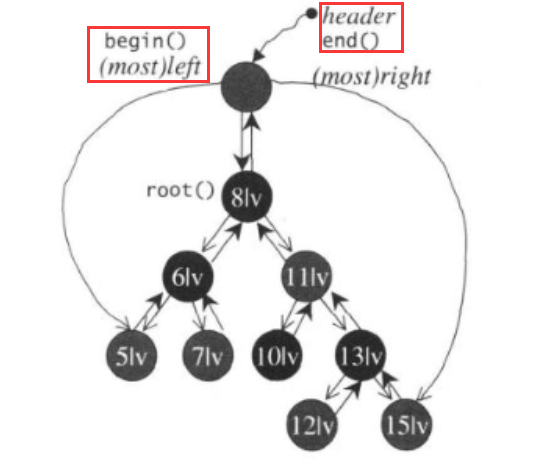
💡STL标准库中,为了简化处理,特别为根节点再设计了一个父节点,名为header。header的左子节点指向最小节点,右子节点指向最大节点。以指向header的左子节点的迭代器为begin(),header为end()。
4.2.2 模拟实现红黑树的迭代器
为了方便实现,我们不完全仿照标准库的实现方法。我们将begin()定义为指向最小节点的迭代器,将end()定义为指向空的迭代器。
- 红黑树迭代器的定义:
//RBTree的节点
template <class V>
struct RBTreeNode
{typedef RBTreeNode<V> Self;V _v;Self* _left;Self* _right;Self* _parent;COLOR _col;RBTreeNode(const V& v):_v(v), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}
};// RBTree的迭代器
// 模板参数设置引用类型Ref和指针类型Ptr, 便于实现const迭代器
template <class V, class Ref, class Ptr>
struct RBTreeIterator
{typedef RBTreeIterator<V, Ref, Ptr> Self;typedef RBTreeNode<V> node;// 构造函数,用指针构造迭代器RBTreeIterator(node* pNode):_pNode(pNode){}// 常见的迭代器接口,类似list的迭代器Ref operator*(){return _pNode->_v;}// it->first ⇒ it->->first ⇒ (&_pNode->_v)->firstPtr operator->(){return &_pNode->_v;}bool operator!=(const Self& it) const{return _pNode != it._pNode;}bool operator==(const Self& it) const{return _pNode == it._pNode;}// 指向红黑树节点的指针node* _pNode;
};
- 红黑树迭代器的自增和自减
- 自增
(++)
红黑树迭代,走的是中序遍历的顺序,因此迭代器的自增要寻找中序遍历顺序(即key值大小顺序)的下一个。以下面这棵红黑树为例。
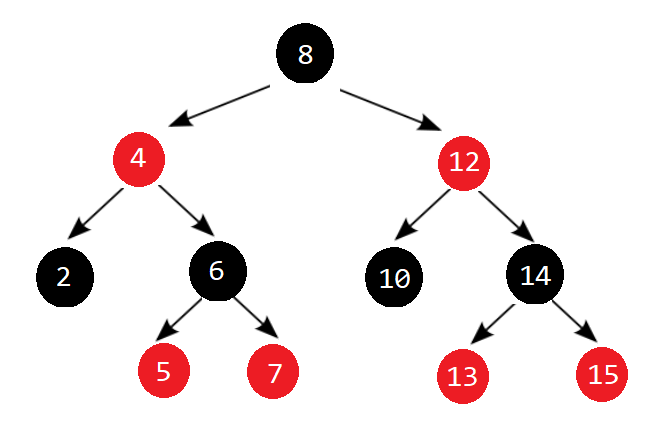
二叉搜索树中,比当前元素大的都在其右边,而红黑树的begin又指向最小(最左)节点,因此其迭代器自增要向右走。由于中序顺序为:
左->根->右,因此从左向右走的途径有:左子树到根,根到右子树两种。也就是说,若当前节点想要向右走,则有可能是右子树的父节点,也可能是某个节点的左子树。那么红黑树的迭代器自增可分为两种情况:
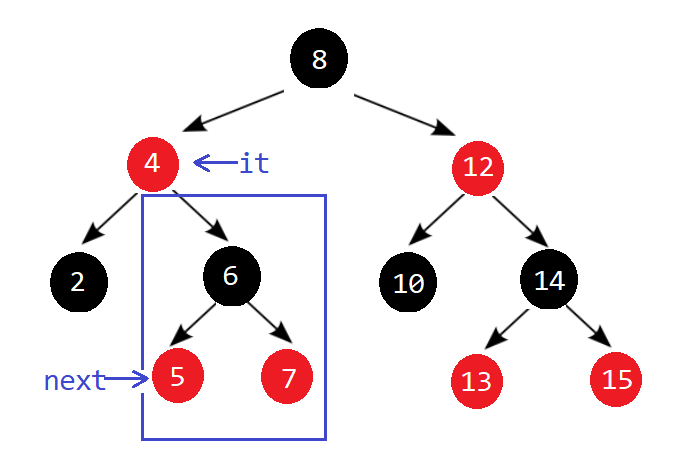
- 右子树存在,则当前节点为其右子树的父节点,下一个节点为右子树的最小节点。
- 右子树不存在,则当前节点存在于某个节点的左子树,下一个节点应是向上找到第一个以当前子树为左子树的节点。
情况1:当前节点右子树存在(根->右)
情况2:当前节点右子树不存在(左->根)
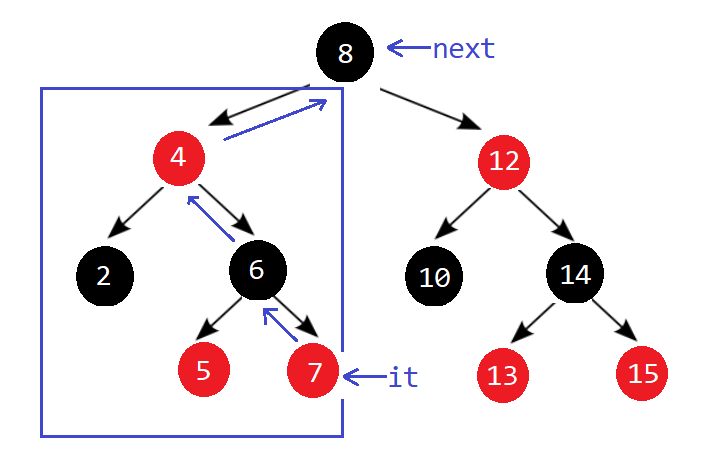
- 自减
(--)
道理和自增类似,可以理解为自增的逆过程。自减要向左走,因此根据中序遍历顺序有两个途径:根->左,右->根。也就是说,若当前节点想要向左走,则有可能是左子树的父节点,也可能是某个节点的右子树。那么红黑树的迭代器自减可分为两种情况:
- 左子树存在,则当前节点为左子树的父节点,下一个节点为左子树的最大(最右)节点。
- 左子树不存在,则当前节点存在于某个节点的右子树,下一个节点应为向上找到第一个以当前子树为右子树的节点。
情况1:当前节点的左子树存在(根->左)
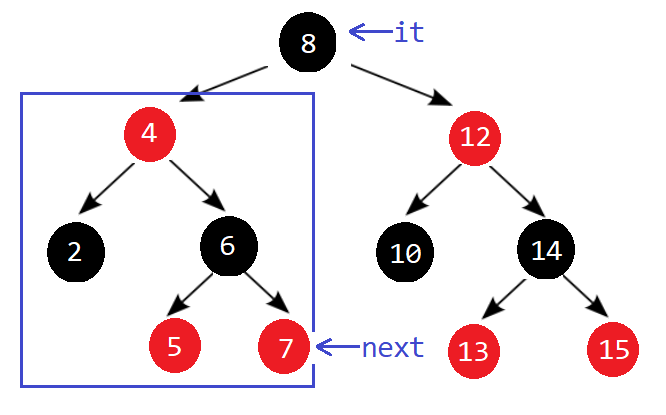
情况2: 当前节点的左子树不存在
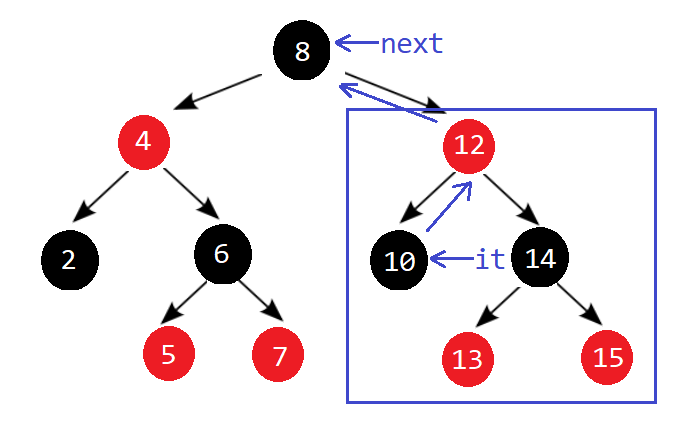
最终,加上自增自减的接口,RBTreeIterator的代码如下:
template <class V, class Ref, class Ptr>
struct RBTreeIterator
{typedef RBTreeIterator<V, Ref, Ptr> Self;typedef RBTreeNode<V> node;RBTreeIterator(node* pNode):_pNode(pNode){}Ref operator*(){return _pNode->_v;}Ptr operator->(){return &_pNode->_v;}// 自增,前置++,返回自增后的迭代器Self& operator++(){if (_pNode == nullptr){assert(false);}if (_pNode->_right) // 根 -> 右{// 找到右子树的最左节点node* minRight = _pNode->_right;while (minRight->_left){minRight = minRight->_left;}_pNode = minRight;}else // 左 -> 根{node* cur = _pNode;node* parent = cur->_parent;while (parent && parent->_left != cur){cur = parent;parent = parent->_parent;}_pNode = parent;}return *this;}// 自减,前置--,返回自减后的迭代器Self& operator--(){if (_pNode == nullptr){assert(false);}if (_pNode->_left) // 找到左边最大节点{node* maxLeft = _pNode->_left;while (maxLeft->_right){maxLeft = maxLeft->_right;}_pNode = maxLeft;}else // 找到孩子是右的根节点{node* cur = _pNode;node* parent = _pNode->_parent;while (parent && parent->_right != cur){cur = parent;parent = parent->_parent;}if (parent)_pNode = parent;elseassert(false); }return *this;}bool operator!=(const Self& it) const{return _pNode != it._pNode;}bool operator==(const Self& it) const{return _pNode == it._pNode;}node* _pNode;
};
- 在RBTree中对迭代器进行定义,并实现
begin()和end()
template <class K, class V, class KeyOfValue>
class RBTree
{typedef RBTreeNode<V> node;public:typedef RBTreeIterator<V, V&, V*> iterator; // 普通迭代器typedef RBTreeIterator<V, const V&, const V*> const_iterator;// const迭代器public://构造函数RBTree():_root(nullptr){}// begin是整棵树的最小节点,即从根节点开始的最左节点iterator begin(){// 最左节点node* left = _root;//_root有可能为空while (left && left->_left){left = left->_left;}return iterator(left);}// end规定为空迭代器iterator end(){return iterator(nullptr);}//const类型RBTree对象调用时,需要返回const迭代器const_iterator begin() const{// 最左节点node* left = _root;//_root有可能为空while (left && left->_left){left = left->_left;}return const_iterator(left);}const_iterator end() const{return const_iterator(nullptr);}// insert的返回值要修改成pair<iterator, bool>,以便map重载[]时使用pair<iterator, bool> insert(const V& v){//具体代码太长,而且与之前实现的RBTree::insert大差不差,只有一点点区别//后面再一并列出,这里主要看的是有关迭代器的代码 //...}
private:node* _root;
};
4.3 map和set的迭代器
💭OK,底层的红黑树提供了迭代器,接下来就要给map和set提供迭代器了。map和set的迭代器各有特点。
- set的迭代器:无法通过迭代器修改元素(因为set的元素就是键值,不能被修改)。因此,在STL中,set的普通迭代器和const迭代器都是const类型,保证了无法通过迭代器修改key值。
- map的迭代器:map的迭代器有普通迭代器和const迭代器两种,普通迭代器可以修改指向的元素的value值,const迭代器则无法修改。
💬综上所述,在map和set中定义迭代器如下:
//set
template <class K>
class set
{struct setKov{const K& operator()(const K& v){return v;}};
public:// 迭代器的定义// 同一个类型typedef typename RBTree<K, K, setKov>::const_iterator iterator;typedef typename RBTree<K, K, setKov>::const_iterator const_iterator;public:// const对象和非const对象(权限缩小)都能调用,且返回的都是const类型的迭代器iterator begin() const{return _t.begin();}iterator end() const{return _t.end();}private:RBTree<K, K, setKov> _t;
};
// map
template <class K, class V>
class map
{struct mapKov{const K& operator()(const pair<const K, V>& kv){return kv.first;}};
public:// 迭代器的定义typedef typename RBTree<K, pair<const K, V>, mapKov>::iterator iterator;// 普通迭代器,可修改value值typedef typename RBTree<K, pair<const K, V>, mapKov>::const_iterator const_iterator;// const迭代器,不可修改value值public:// 普通对象调用返回普通迭代器,const对象调用返回const迭代器iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end() const{return _t.end();}
private:RBTree<K, pair<const K, V>, mapKov> _t;
};
4.4 map和set的插入操作
map的插入操作,很简单,直接复用红黑树的插入即可。
template <class K,class V>
class map
{
//...pair<iterator, bool> insert(const pair<const K, V>& kv){return _t.insert(kv);}//重载方括号V& operator[](const K key){pair<iterator, bool> p = _t.insert(make_pair(key, V()));return (p.first)->second;}
//...
}
而set的插入操作就需要注意一些小小的细节,如果直接复用红黑树的插入。
template <class K>
class set
{
//...pair<iterator, bool> insert(const K& k){return _t.insert(v);//error}
//...
}
这里面,_t.insert(v)返回的pair中的迭代器是普通迭代器,而set::insert返回值接收时,pair中的迭代器是const迭代器。这里会出现类型不匹配的问题。因此我们需要一个将普通迭代器转化为const迭代器的 “中转站”。
⭕STL中是这样设计的,在RBTreeIterator定义一个iterator类型,它始终是普通迭代器类型,无论Self是普通迭代器还是const迭代器。借此,可以写一个函数
RBTreeIterator(const iterator& it),对于普通迭代器来说,它只是一个拷贝构造;而对于const迭代器来说,它是一个能够用普通迭代器构造const迭代器的构造函数。这样一来便实现了将普通迭代器转化const迭代器的目的。
template <class V, class Ref, class Ptr>
struct RBTreeIterator
{typedef RBTreeIterator<V, Ref, Ptr> Self;typedef RBTreeIterator<V, V&, V*> iterator;// 固定的普通迭代器类型typedef RBTreeNode<V> node;RBTreeIterator(node* pNode):_pNode(pNode){}// 拷贝构造编译器会默认实现//RBTreeIterator(const Self& it)// :_pNode(it._pNode)//{}// 普通迭代器->const迭代器// 对于普通迭代器:拷贝构造// 对于const迭代器:用普通迭代器构造const迭代器的构造函数RBTreeIterator(const iterator& it):_pNode(it._pNode){}//...
}
💬set的插入操作正确示例:
template <class K>
class set
{
//...// 返回值的iterator是const_iterator,不能直接接收_t.insert的返回值,中间要有一层// 普通迭代器转化为const迭代器pair<iterator, bool> insert(const K& v){auto pRet = _t.insert(v); // 先接受_t.insert的返回值iterator it = pRet.first;// 用普通迭代器构造const迭代器return make_pair(it, pRet.second);// 再用const迭代器构造pair,最后返回}
//...
}
4.5 map和set最终实现
💬 完整的map和set模拟实现代码总览:
// settemplate <class K>
class set
{struct setKov{const K& operator()(const K& v){return v;}};public:typedef typename RBTree<K, K, setKov>::const_iterator iterator;typedef typename RBTree<K, K, setKov>::const_iterator const_iterator;public:pair<iterator, bool> insert(const K& v){auto pRet = _t.insert(v);iterator it = pRet.first;return make_pair(it, pRet.second);}iterator begin() const{return _t.begin();}iterator end() const{return _t.end();}private:RBTree<K, K, setKov> _t;
};
// maptemplate <class K, class V>
class map
{struct mapKov{const K& operator()(const pair<const K, V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, mapKov>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, mapKov>::const_iterator const_iterator;public:pair<iterator, bool> insert(const pair<const K, V>& kv){return _t.insert(kv);}V& operator[](const K key){pair<iterator, bool> p = _t.insert(make_pair(key, V()));return (p.first)->second;}iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end() const{return _t.end();}private:RBTree<K, pair<const K, V>, mapKov> _t;
};
完整的红黑树、map、set代码及其测试代码已经存放在我的gitee上了,有需要的读者可以自取噢~
📃map和set博客的代码
- 完结撒花🎊写作不易,如果觉得本文对你有帮助,不妨点点关注支持一下博主!


