0205顶点对可达性及小结-有向图-数据结构和算法(Java)

1 顶点对的可达性
在有向图中如果两个顶点v和w是强连通的,那么即存在从v到w到路径也存在一条从w到v的路径。如果一对非连通顶点, 不可能两条都存在。
顶点对的可达性。给定一幅有向图,回答“是否存在一条从一个给定顶点v到另外一个顶点w到路径?等类似问题
如下图4-1所示,它展示了下面这个基本的概念
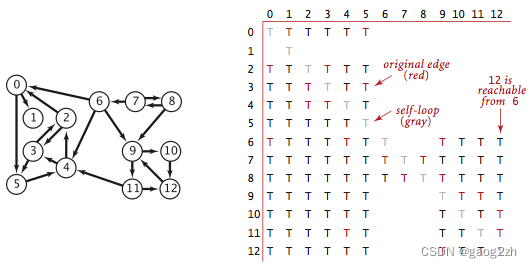
有向图G中的传递闭包是由相同的顶点组成的另一幅有向图,在传递闭包中存在一条从v指向w的边当且仅当在G中w是从v可达的。
根据约定,每个顶点对于自己都是可达的,因此传递闭包含有V个自环。示例有向图只有22条有向边,但它的传递闭包包含有169条有向边中的102条。一般来说,一幅有向图的传递闭包中所含有的边都比原图中多得多。
2 API及实现
顶点对可达性API如下
| public class | TransitiveClosure | |
|---|---|---|
| TransitiveClosure(Digraph digraph) | 预处理构造函数 | |
| public boolean | Reachable(itn v, int w) | 顶点w是从v可达的吗 |
实现代码如下2-1所示:
package com.gaogzhen.datastructure.graph.directed;import edu.princeton.cs.algs4.Digraph;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;/* 顶点对的可达性* @author gaogzhen*/
public class TransitiveClosure {/* 顶点v起点的可达有向图*/private DirectedDFS[] tc;/* 计算有向图G的传递闭包* @param G 给定有向图*/public TransitiveClosure(Digraph G) {tc = new DirectedDFS[G.V()];for (int v = 0; v < G.V(); v++) {tc[v] = new DirectedDFS(G, v);}}/* 顶点w是从v可达的吗* @param v 给定顶点* @param w 目标顶点* @return {@code true} 顶点w从顶点v可达,{@code false} 否则* @throws IllegalArgumentException unless {@code 0 <= v < V}* @throws IllegalArgumentException unless {@code 0 <= w < V}*/public boolean reachable(int v, int w) {validateVertex(v);validateVertex(w);return tc[v].marked(w);}/* 校验顶点v* @param v 顶点v*/private void validateVertex(int v) {int V = tc.length;if (v < 0 || v >= V) {throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));}}
}
测试代码2-2如下:
public static void testTransitiveClosure() {String path = System.getProperty("user.dir") + File.separator + "asserts/tinyDG1.txt";In in = new In(path);Digraph G = new Digraph(in);TransitiveClosure tc = new TransitiveClosure(G);// print headerStdOut.print(" ");for (int v = 0; v < G.V(); v++) {StdOut.printf("%3d", v);}StdOut.println();StdOut.println("--------------------------------------------");// print transitive closurefor (int v = 0; v < G.V(); v++) {StdOut.printf("%3d: ", v);for (int w = 0; w < G.V(); w++) {if (tc.reachable(v, w)) {StdOut.printf(" T");} else {StdOut.printf(" ");}}StdOut.println();}
}
测试结果:
0 1 2 3 4 5 6 7 8 9 10 11 12
--------------------------------------------0: T T T T T T 1: T 2: T T T T T T 3: T T T T T T 4: T T T T T T 5: T T T T T T 6: T T T T T T T T T T T7: T T T T T T T T T T T T T8: T T T T T T T T T T T T T9: T T T T T T T T T T10: T T T T T T T T T T11: T T T T T T T T T T12: T T T T T T T T T T
3 分析
- 实现简单
- 不适用于大型有向图
- 构造函数所需空间和V2V^2V2成正比,所需的时间和V(V+E)成正比
用远小于平方级别的空间支持常数级别的查询的一般解决方案仍然是有待解决的研究问题,并且有实际意义:例如,除非这个问题得到解决,对于像互联网这样的巨型有向图,否则无法有效解决其中的顶点对可达性问题。
4 有向图小结
本节中,我们介绍了有向边和有向图并强调了有向图处理算法,涵盖以下几个方面:
- 有向图的术语;
- 有向图的算法和表示在本质上和无向图上是相同的,但部分有向图更复杂;
- 有向环、有向无环图、拓扑排序和优先级限制下的调度问题;
- 有向图的可达性、路径和强连通性。
如下表4-1所示总结了我们学习过的各种有向图算法的实现,是下面我们学习更加复杂算法的基础:
| 问题 | 解决方法 | 参阅 |
|---|---|---|
| 单点和多点的可达性 | DirectedDFS | |
| 单点有向路径 | DepthFirstDirectedPaths | |
| 单点最短有向路径 | BreadthFirstDirectedPaths.java | |
| 有向环检测 | DirectedCycle.java | |
| 深度优先的顶点排序 | DepthFirstOrder.java | |
| 优先级限制下的调度问题 | Topological.java | |
| 拓扑排序 | Topological.java | |
| 强连通性 | KosarajuSharirSCC.java | |
| 顶点对的可达性 | TransitiveClosure.java |
结语
如果小伙伴什么问题或者指教,欢迎交流。
❓QQ:806797785
⭐️源代码仓库地址:https://gitee.com/gaogzhen/algorithm
参考链接:
[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法:第4版[M].北京:人民邮电出版社,2012.10.p384-385.


