前言

1、打家劫舍
2、打家劫舍Ⅱ
3、打家劫舍Ⅲ
4、链表中的下一个更大节点

一、打家劫舍（力扣198）【相邻两间房不能偷】

分析：

注意：dp[i]表示第i间房时，此时已经偷到的最大金额
每一间房都有偷和不偷两种情况
偷：需要确保不触发警报 dp[i-2]+nums[i]
不偷：dp[i-1]；
dp[i] = Math.max(dp[i-2]+nums[i], dp[i-1]);

class Solution {public int rob(int[] nums) {int[]dp = new int[nums.length];if(nums.length ==1){return nums[0];}dp[0] = nums[0];dp[1] = Math.max(nums[0],nums[1]);for( int i=2;i<nums.length;i++){//前一间没偷  前一间偷了dp[i] = Math.max(dp[i-2]+nums[i],dp[i-1]);}return dp[nums.length-1];}
}

二、打家劫舍 II（力扣213）【围成一圈 相邻两间房不能偷】

分析：
分为左右两个部分 例如 1，2，3
可以分为左边：1，2；
右边：2，3；
对于左右两边分别进行1的操作，最后求最大值即可。

为什么要分两边： 原因在于首尾相连，如果包含首元素，不管偷不偷首元素，都不能包含尾元素。
同理 如果包含尾元素，不管偷不偷尾元素，都不能包含首元素。

需要额外处理 nums.length==2时的情况，因为不会执行右半部分，所以直接返回前两个元素的较大值即可

		if(nums.length==2){return Math.max(nums[0],nums[1]);}

class Solution {
public int rob(int[] nums) {if(nums.length==1){return nums[0];}int[] dp = new int[nums.length];int[] dp2 = new int[nums.length];dp[0] = nums[0];if(nums.length==2){return Math.max(nums[0],nums[1]);}dp[1] = Math.max(nums[0],nums[1]);//分为左右两个部分//左半部分for(int i=2;i<nums.length-1;i++){dp[i] = Math.max(dp[i-2]+nums[i],dp[i-1]);}//右半部分dp2[1] = nums[1];dp2[2] = Math.max(nums[1],nums[2]);for(int j=3;j<nums.length;j++){dp2[j] = Math.max(dp2[j-2]+nums[j],dp2[j-1]);}return Math.max(dp[nums.length-2],dp2[nums.length-1]);}
}

三、打家劫舍 III（力扣337）【树形DP】

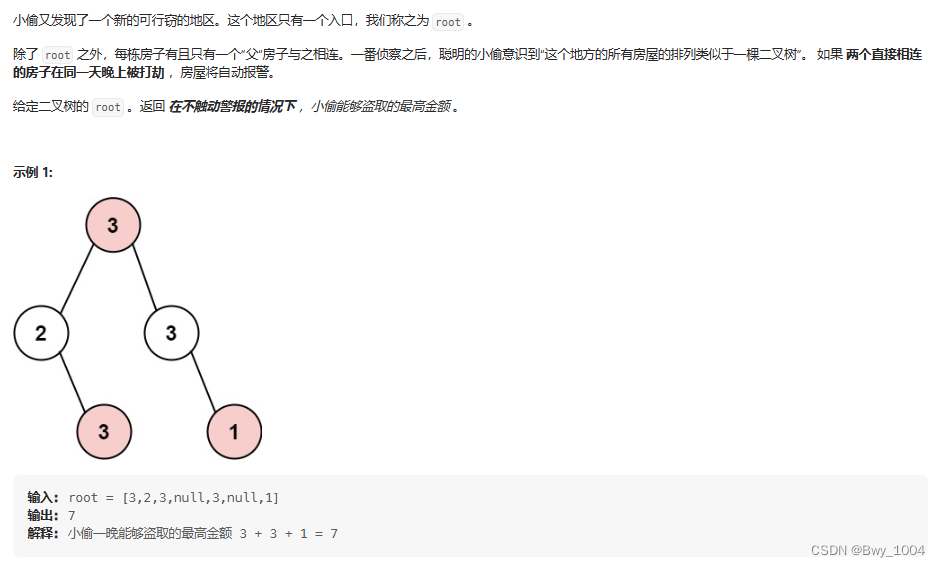
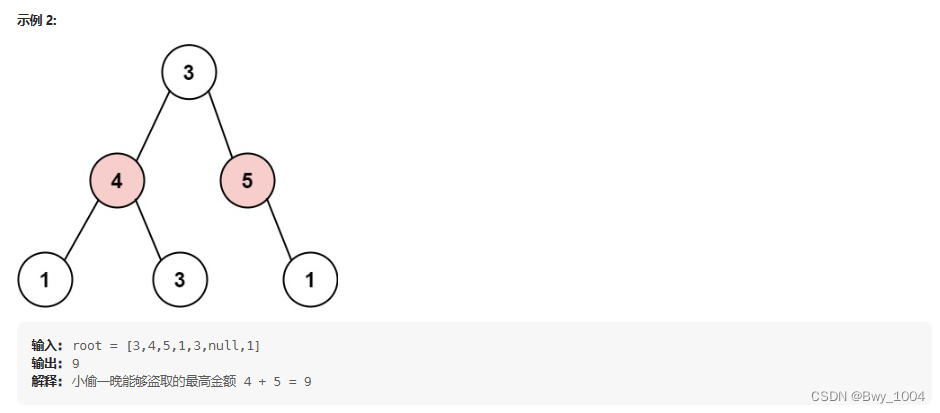
分析：
注意选清楚二叉树的遍历方式，
其次，dp[]数组只需要记录当前结点偷与不偷的两个状态
dp[]数组不需要记录是哪一个结点，交给递归去做

注意：当不偷根节点时，左右结点不是必须要偷，左右结点也可以不偷，取决于左右节点偷的值大还是不偷的值大。

        //偷根节点val[0] = current.val+left[1]+right[1];//不偷根节点val[1] = Math.max(left[0],left[1])+Math.max(right[0],right[1]);

/* Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public  int rob(TreeNode root) {int[] res = new int[2];res = robTree(root);return Math.max(res[0],res[1]);}public  int[] robTree(TreeNode current){int[] val = new int[2];if(current == null) return val;int[] left = new int[2];int[] right = new int[2];left = robTree(current.left);right = robTree(current.right);//偷根节点val[0] = current.val+left[1]+right[1];//不偷根节点val[1] = Math.max(left[0],left[1])+Math.max(right[0],right[1]);return val;}
}

每日一题day81：链表中的下一个更大节点（力扣1019）

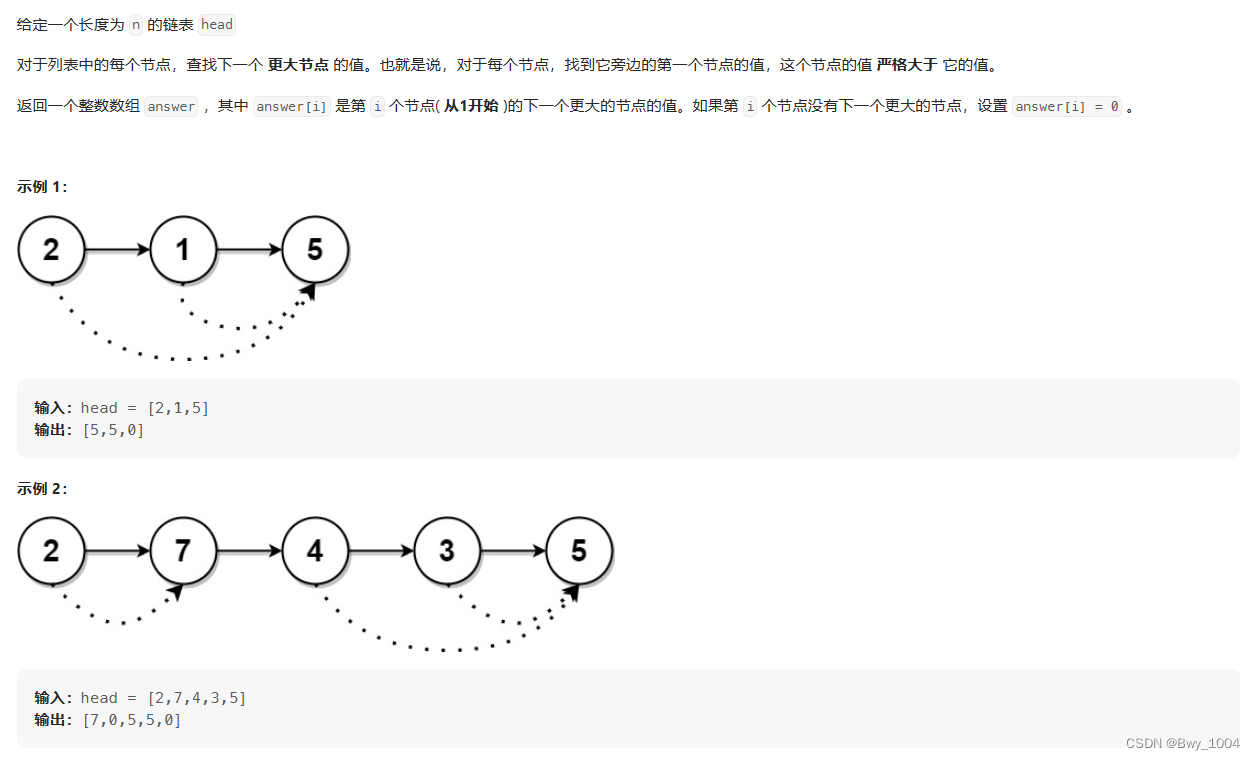
分析：
典型单调栈

public static int[] nextLargerNodes(ListNode head) {//单调栈？//求链表长度if(head == null) return null;ListNode cur = head;int size =1;while(cur.next!=null){cur = cur.next;size++;}int[] temp = new int[size];int[] res = new int[size];cur = head;int i = 0;while(cur!=null){temp[i] = cur.val;cur = cur.next;i++;}Stack<Integer> stack = new Stack<>();stack.push(0);for(int j=1;j<size;j++){//栈内是递增的if(!stack.isEmpty() && temp[stack.peek()]>=temp[j]){//直接入栈即可stack.push(j);}while(!stack.isEmpty() && temp[stack.peek()]<temp[j]){i = stack.pop();res[i] = temp[j];}stack.push(j);}return res;}