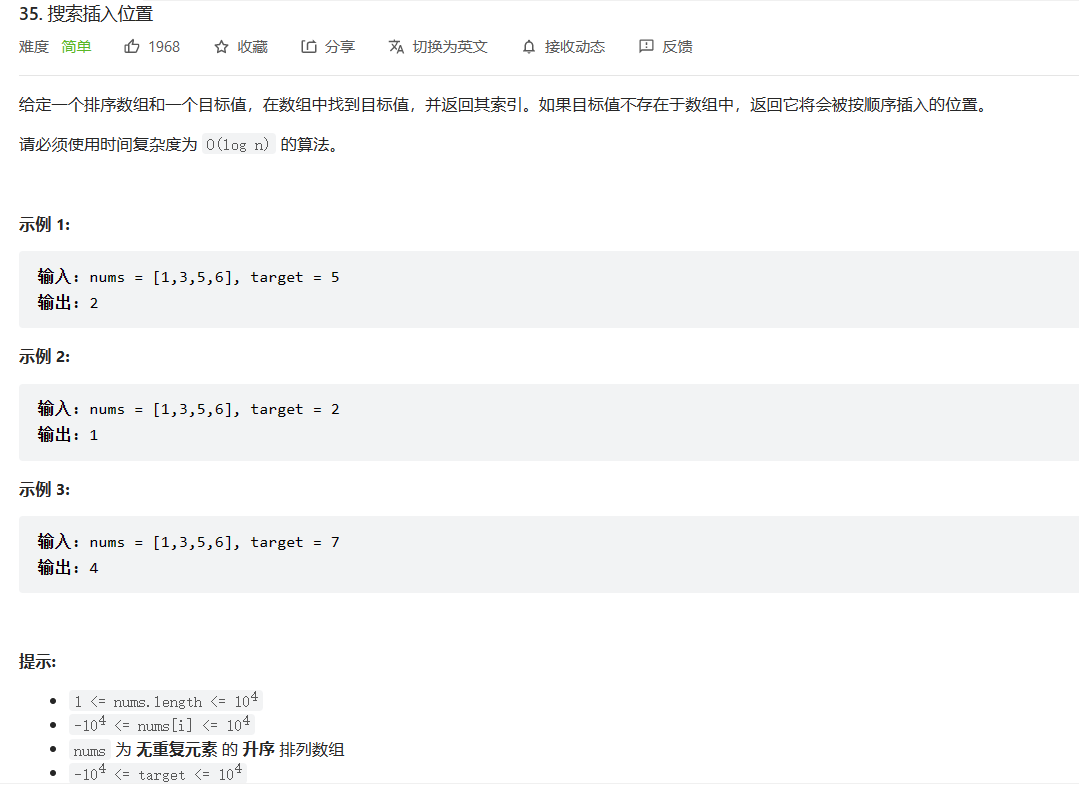
第一部分：题目描述

🏠 链接：35. 搜索插入位置 - 力扣（LeetCode）

⭐ 难度：简单

第二部分：思路分析

我们可以先看下普通二分查找的代码：满足了查到返回索引，查不到返回-1

    public int search(int[] nums, int target) {int left = 0;int right = nums.length - 1;int mid;while (left <= right) {// 得到中间索引/*考虑到 left+right 的值可能会超过 int可表示 的最大值，我们不再对他们的和直接除以2我们知道 除以2 的操作可以用 位运算 >>1 来代替但还不够，由于 (left+right) 值溢出表示负数，>>1 只是做 除以2 操作，最高位符号位不变，依旧为1表示负数，负数除以2依旧是负数这时候我们可以修改为 无符号右移 >>>1 ，低位溢出，高位补0，那么最高位符号位为0就表示正数了*/mid = (left + right) >>> 1;if (target < nums[mid]) {// 如果目标值小于中间值right = mid - 1;} else if (nums[mid] < target) {// 如果目标值大于中间值left = mid + 1;} else {return mid;}}return -1;}

而这道题目的要求是：查到返回索引，查不到返回应该插入位置的索引。

我们可以这样来分析：

1. 如果能够查询得到，还是走原来的逻辑，即 else 块中的 return mid。

2. 如果查询不到，你首先必须肯定这样一件事：

   • 全部搜索完还查找不到时 while 循环会退出

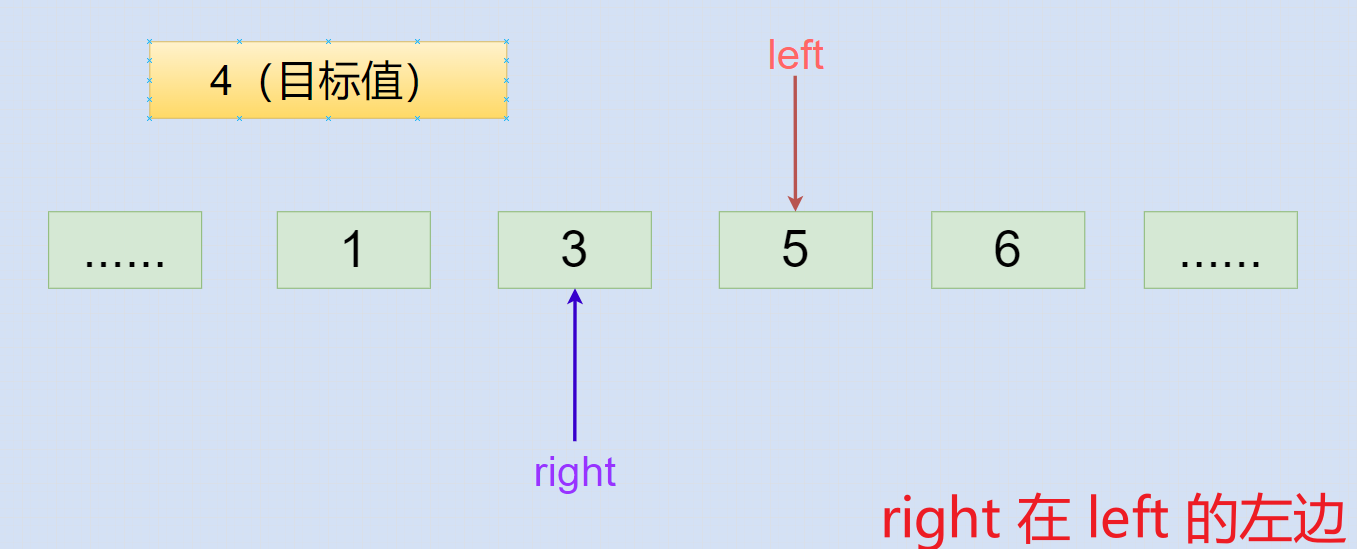
   • 具体是为什么会退出呢？==》left <= right 的条件不成立，即 left > right，更具体的说是 right + 1 == left 了。

     

3. 紧接着，我们又必须赞成一件事：

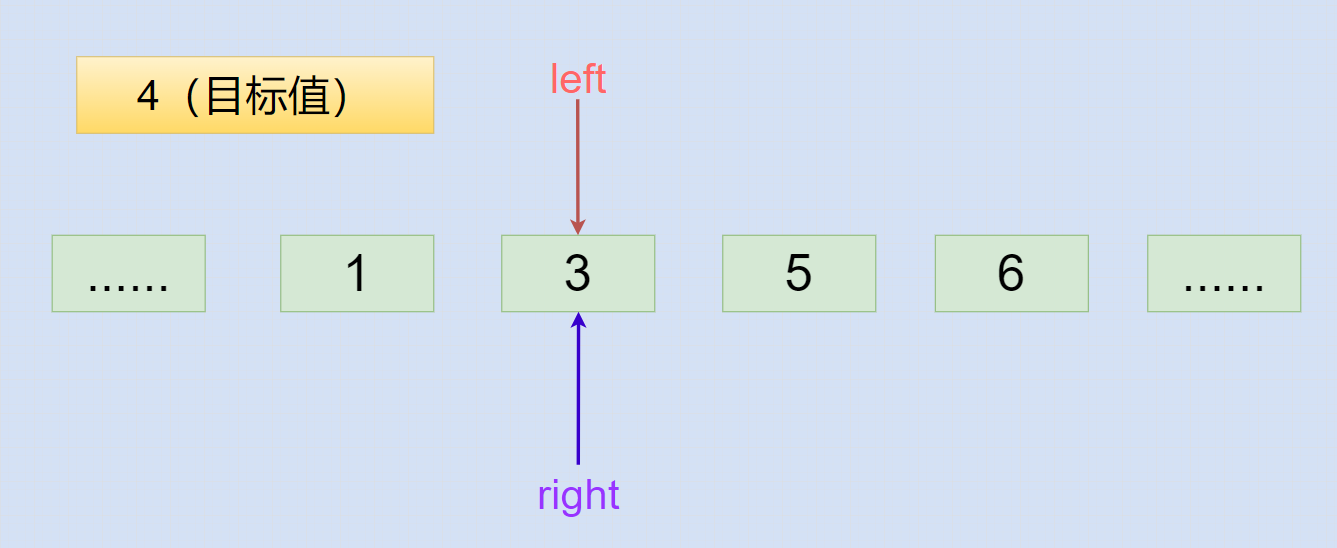
   • 在 left > right ，即 right + 1 == left 之前的while循环中，肯定有 left == right 成立

     

   • 在以 left == right 为循环条件的循环体中，进行了 if 语句的right指针向左移动 或者 else-if 语句的left指针向右移动，而导致出现了 right + 1 == left ，自此循环退出。

4. 那么这个时候就很好分析了，我们知道了最后一次循环时的循环条件是 left == right，至于是 if 语句的right指针向左移动 还是 else-if 语句的left指针向右移动 都有可能，我们分这两种情况进行分析：

   • if 语句的right指针向左移动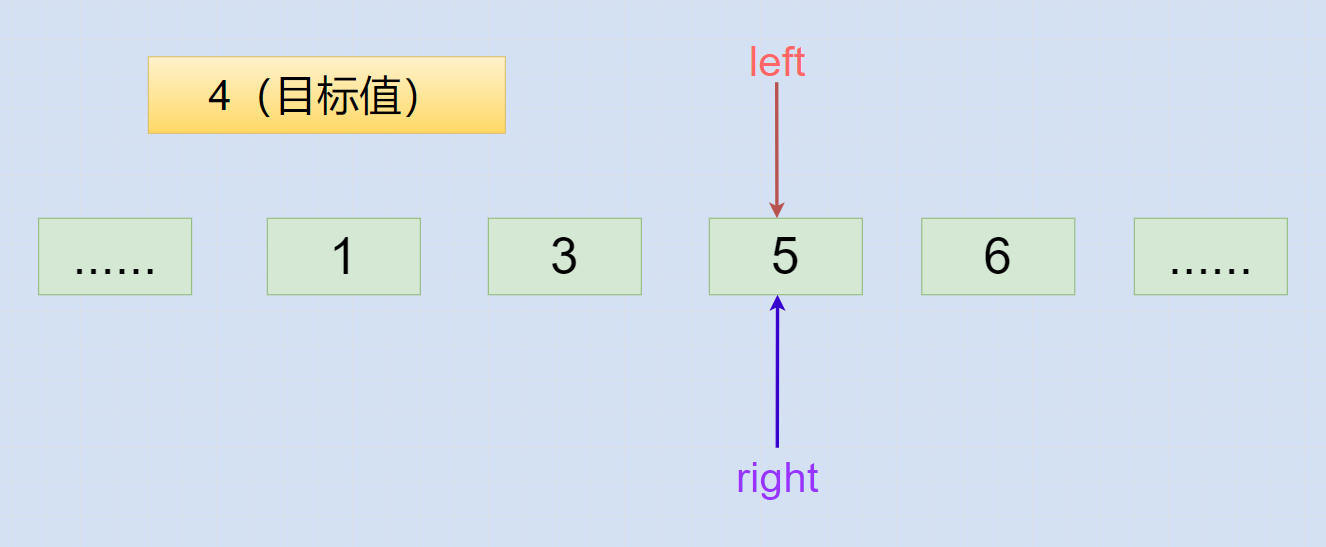

     

     当目标值小于 中间索引mid对应值 时，会走 if 语句导致 right 指针左移，自此 while 循环会结束。

     

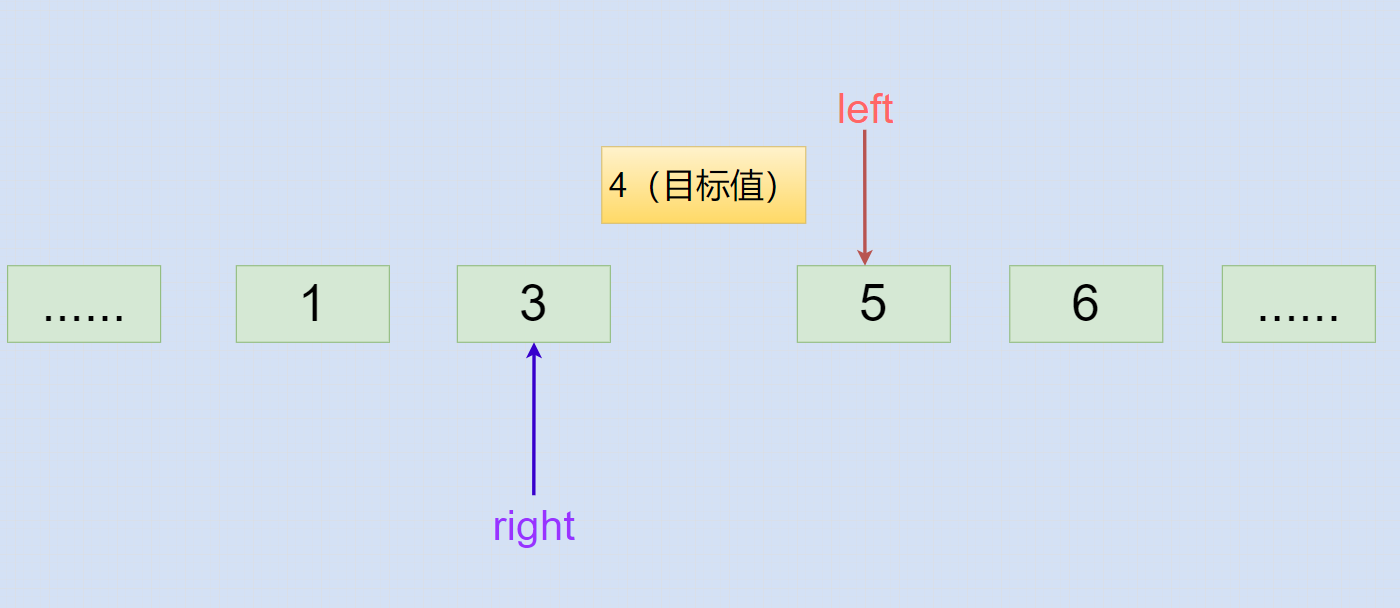
     对于是一个从小到大排序的升序数组，我们知道插入位置应该放在 中间索引mid 的前面，即插入位置应当就是 当前中间索引mid ，那不就是 left指针 的位置吗？

   • else-if 语句的left指针向右移动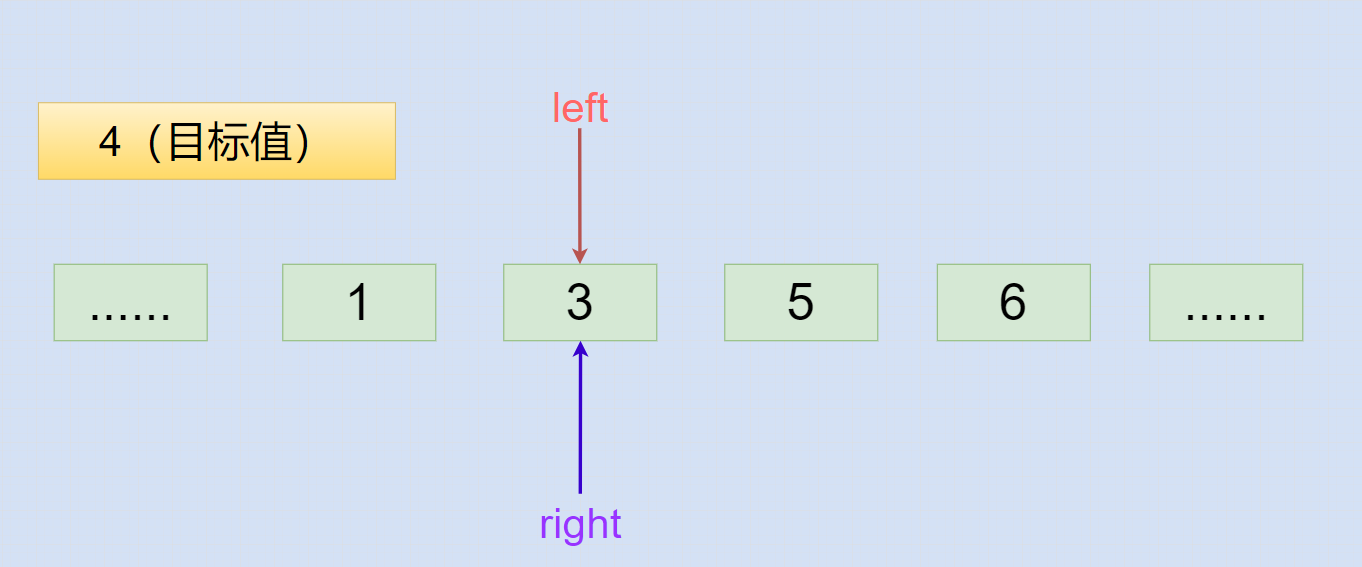

     

     当目标值大于 中间索引mid对应值 时，会走 else-if 语句导致 left 指针右移，自此 while 循环会结束。

     

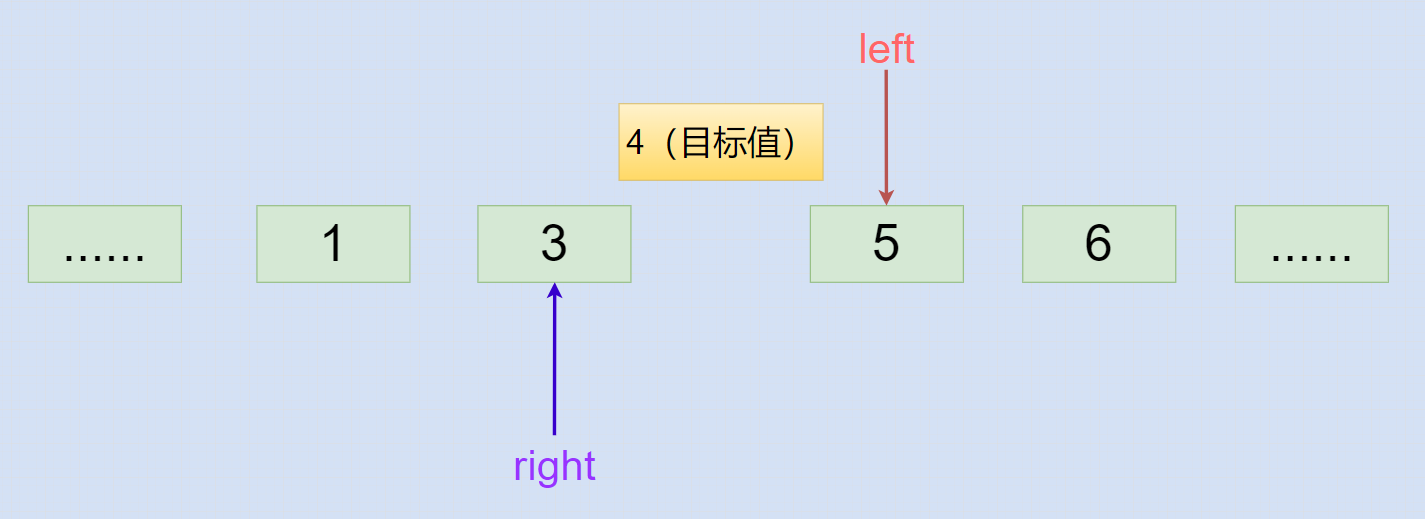
     对于是一个从小到大排序的升序数组，我们知道插入位置应该放在 中间索引mid 的后面，而最后一次循环操作后 left 指针从原来的 mid 位置右移了一位，那插入位置不就是最终 left指针 的位置吗？

5. 因此，综上所述

   • 查找到了，就是原二分查找的 return mid
   • 未查找到，就是最终 left指针 的位置。 因此只需要将 return -1 改为 return left 即可。

第三部分：代码实现

    public int searchInsert(int[] nums, int target) {int left = 0;int right = nums.length - 1;int mid;while (left <= right) {// 得到中间索引/*考虑到 left+right 的值可能会超过 int可表示 的最大值，我们不再对他们的和直接除以2我们知道 除以2 的操作可以用 位运算 >>1 来代替但还不够，由于 (left+right) 值溢出表示负数，>>1 只是做 除以2 操作，最高位符号位不变，依旧为1表示负数，负数除以2依旧是负数这时候我们可以修改为 无符号右移 >>>1 ，低位溢出，高位补0，那么最高位符号位为0就表示正数了*/mid = (left + right) >>> 1;if (target < nums[mid]) {// 如果目标值小于中间值right = mid - 1;} else if (nums[mid] < target) {// 如果目标值大于中间值left = mid + 1;} else {return mid;}}return left;}

第四部分：拓展-Java底层源码对二分查找的实现

⭐ 在 Arrays 类中的方法 binarySearch0(int[] a, int fromIndex, int toIndex, int key)，源码如下：

    /* 使用二进制搜索算法在指定的整数数组中搜索指定的值。在进行此调用之前，必须对数组进行排序（按方法排序 sort(int[]) ）。* 如果未排序，则结果未定义。如果数组包含多个具有指定值的元素，则无法保证会找到哪个元素。* 参数：* 		a – 要搜索的数组 *		key – 要搜索的值* 返回：搜索键的索引（如果它包含在数组中）;否则，（ -（插入点）-1）。* 插入点定义为将键插入数组的 点 ：第一个元素的索引大于键，如果数组中的所有元素都小于指定的键，则为 a.length 。* 请注意，这保证了当且仅当找到键时返回值将为 >= 0。*/public static int binarySearch(int[] a, int key) {return binarySearch0(a, 0, a.length, key);}// Like public version, but without range checks.private static int binarySearch0(int[] a, int fromIndex, int toIndex,int key) {int low = fromIndex;int high = toIndex - 1;while (low <= high) {int mid = (low + high) >>> 1;int midVal = a[mid];if (midVal < key)low = mid + 1;else if (midVal > key)high = mid - 1;elsereturn mid; // key found}return -(low + 1);  // key not found.}

第五部分：拓展-利用Arrays实现二分查找目标值，不存在则插入

    public static void main(String[] args) {// 二分查找目标值，不存在则插入/*原始数组：[2,5,8]查找目标值：4查询不到，返回的结果为 r = -待插入点索引-1在这里带插入点索引为 1，对应 r = -2那么我们分成这几步来进行拷贝：- 1.新建数组,大小为原数组的大小+1：         [0,0,0,0]- 2.将待插入点索引之前的数据放入新数组：     [2,0,0,0]- 3.将目标值放入到待插入点索引的位置：       [2,4,0,0]- 4.将原数组后面的数据都相继拷贝到新数组后面： [2,4,5,8]*/// 定义原数组与目标值int[] oldArray = {2, 5, 8};int target = 4;// 搜索目标值4，没有找到，返回结果为 r =  -待插入点索引-1，这里的 r=-2int r = Arrays.binarySearch(oldArray, target);// r < 0 说明没有找到目标值，就插入if (r < 0) {// 获取待插入索引int insertIndex = -r - 1;// 1.新建数组,大小为原数组的大小+1int[] newArray = new int[oldArray.length + 1];// 2.将待插入点索引之前的数据放入新数组System.arraycopy(oldArray, 0, newArray, 0, insertIndex);// 3.将目标值放入到待插入点索引的位置newArray[insertIndex] = target;// 4.将原数组后面的数据都相继拷贝到新数组后面System.arraycopy(oldArray, insertIndex, newArray, insertIndex + 1, oldArray.length - insertIndex);System.out.println(Arrays.toString(newArray));}}

第六部分：拓展-(left + right) >>> 1的分析

在本文中我使用的是 (left + right) >>> 1 来代替 (left + right) / 2，目的是解决 left + right 超过int最大值 的问题。

我们先来举个模拟问题的发生：

    public static void main(String[] args) {// 模拟 二分查找中的 leftint left = 100;// 模拟 二分查找中的 rightint right = Integer.MAX_VALUE - 1;// 此时 left+right 的值超过了 int范围 的最大值，导致 left + right 的结果为负数// 然后对负数进行除以2操作，结果依旧为负数int mid = (left + right) / 2;// 输出结果为 -1073741775System.out.println(mid);}

那如何解决这个问题呢？我们可以使用 位运算 来代替 /2 的操作。

• 算数右移 >> ：低位溢出，符号位不变，并用符号位补溢出的高位。

• 逻辑右击（无符号右移）>>>：低位溢出，高位补0。

由于最高位符号位为0表示该数为正数，因此相比于 >> 做到了能将一个 负数 无符号右移后变成 正数。

第七部分：方法-返回≥目标的最靠左索引

除了使用第三部分的代码实现方法，还可以使用 Leftmost 方式解决该问题：

具体解释参考：力扣704二分查找：思路分析+代码实现（递归与非递归）_是谢添啊的博客-CSDN博客

    public int searchInsert(int[] array, int target) {int left = 0;int right = array.length - 1;int mid;while (left <= right) {mid = (left + right) >>> 1;if (target <= array[mid]) {// array[mid] 满足大于等于目标值，因此可以记录right = mid - 1;} else if (array[mid] < target) {// 目标值大于中间索引值，缩小左范围left = mid + 1;}}// 返回结果return left;}