C#,码海拾贝(11)——拉格朗日(Lagrange)三点式曲面插值算法,《C#数值计算算法编程》源代码升级改进版

本文开始是曲面插值(Surface Interpolation,也称作:二维插值,二元插值)。
数值计算三点式
数值计算三点式是一种常见的数值计算方法,它是通过对已知函数在某个点及其左右两个点处的函数值进行数值插值,得到该函数在该点处的近似值。数值计算三点式是数值计算中最基本的插值方法之一,也是其它高级插值方法的基础。
数值计算三点式的基本思想是,通过连接已知点,构造一个二次函数,来近似估计未知点处的函数值。如果已知函数在某个点x0处的函数值f(x0),以及其左右两个点x1和x2处的函数值f(x1)和f(x2),则可以构造一个二次函数,通过这个二次函数来估计函数在任意一个x处的函数值。具体来说,可以采用拉格朗日插值法或牛顿插值法求解。
拉格朗日插值(Lagrange interpolation)是一种多项式插值方法,指插值条件中不出现被插函数导数值,过n+1个样点,满足如下图的插值条件的多项式。也叫做拉格朗日公式。
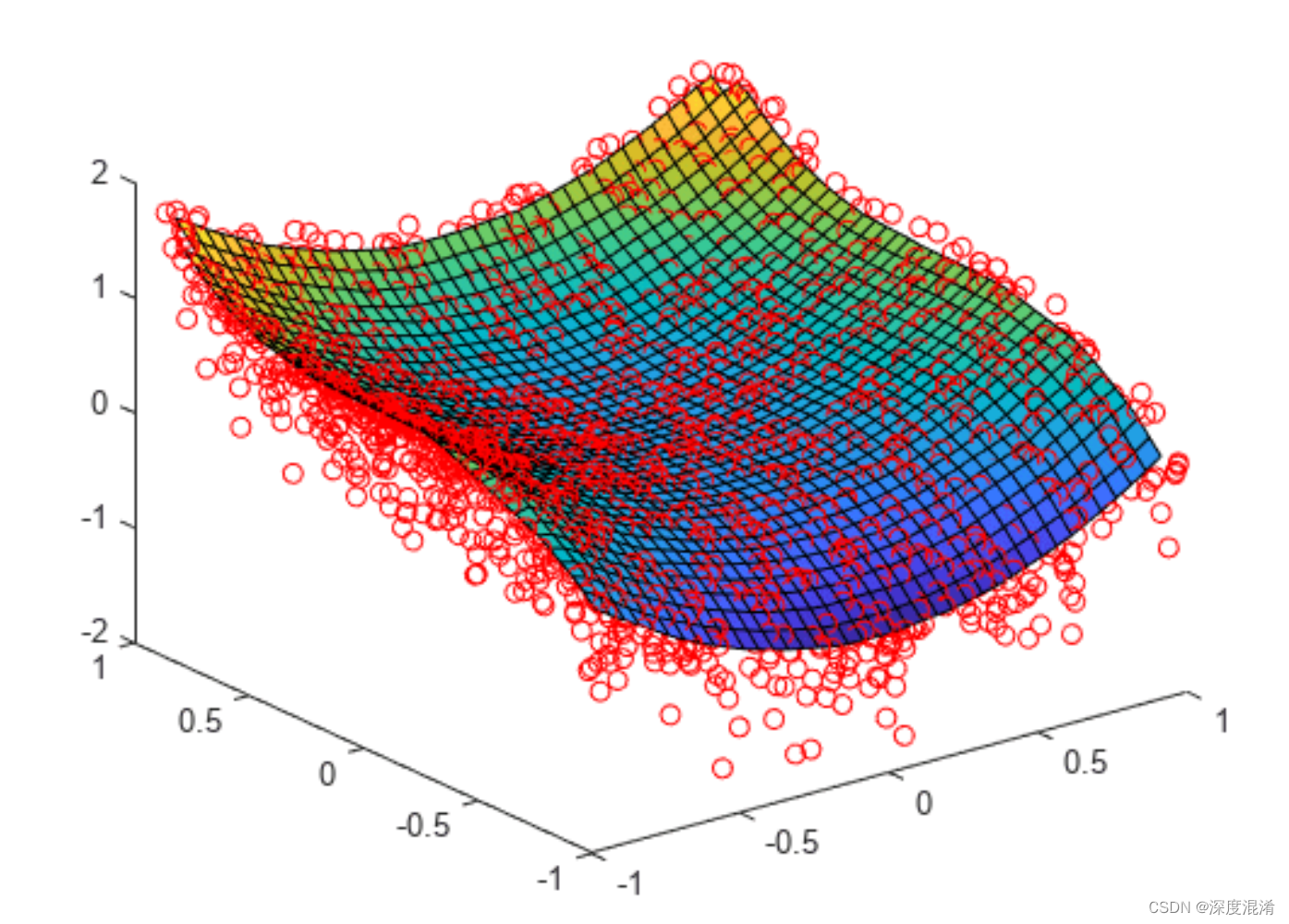
对于一维曲线的插值,一般用到的函数yi=interp1(X,Y,xi,method) ,其中method包括nearst,linear,spline,cubic。
对于二维曲面的插值,一般用到的函数zi=interp2(X,Y,Z,xi,yi,method),其中method也和上面一样,常用的是cubic。
多维曲面法是用来描绘不规则曲面的一种插值技术,经常用于地形学的插值计算中.此方法利用以二次函数为基函数所建立的曲面来描述整个对象,其中最常用的是圆形双叶双曲线.由于描述该方法的控制方程恒有解,因此又称该方法是双调和的.
拟合与插值的区别:
1、在含义上不同:插值是指函数在多个离散点上的函数值或导数信息。通过求解函数中待定形式和待定系数的插值函数,该函数满足给定离散点的约束。
插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。
拟合是指将平面上的一系列点与光滑曲线连接起来。因为这个曲线有无数的可能性,所以有多种拟合方法。拟合曲线一般可以用函数来表示。根据不同的功能,有不同的拟合名称。
常用的拟合方法有如最小二乘曲线拟合法等,在MATLAB中也可以用polyfit 来拟合多项式。
2、在图像上是不同:图像中的插值必须通过数据,图像中的拟合必须得到最接近的结果,这取决于整体效果。MATLAB做曲线拟合可以通过内建函数或者曲线拟合工具箱(Curve Fitting Toolbox)。这个工具箱集成了用MATLAB建立的图形用户界面(GUIs)和M文件函数。
利用这个工具箱可以进行参数拟合(当想找出回归系数以及他们背后的物理意义的时候就可以采用参数拟合),或者通过采用平滑样条或者其他各种插值方法进行非参数拟合(当回归系数不具有物理意义并且不在意他们的时候,就采用非参数拟合方法)。
利用这个界面,可以快速地在简单易用的环境中实现许多基本的曲线拟合。
拟合与插值的区别:
1、在含义上不同:插值是指已知某函数的在若干离散点上的函数值或者导数信息,通过求解该函数中待定形式的插值函数以及待定系数,使得该函数在给定离散点上满足约束。
而拟合是指,拟合就是把平面上一系列的点,用一条光滑的曲线连接起来。因为这条曲线有无数种可能,从而有各种拟合方法。拟合的曲线一般可以用函数表示,根据这个函数的不同有不同的拟合名字。
2、在图像上是不同:插值在图像是一定得过了数据的才行;拟合在图像上是必须要得到最接近得结果,是要看总体的效果。
3、在几何意义上不同:拟合是给定了空间中的一些点,找到一个已知形式未知参数的连续曲面来最大限度地逼近这些点;而插值是找到一个(或几个分片光滑的)连续曲面来穿过这些点。
using System;
using System.Drawing;
using System.Collections;
using System.Collections.Generic;namespace Zhou.CSharp.Algorithm
{/// <summary>/// 插值计算类Interpolation.cs/// 作者:周长发/// 改编:深度混淆/// https://blog.csdn.net/beijinghorn/// </summary>public static partial class Interpolation{/// <summary>/// 二维三点插值/// </summary>/// <param name="x">一维数组,长度为n,存放给定n x m 个结点x方向上的n个值x(i)</param>/// <param name="y">一维数组,长度为m,存放给定n x m 个结点y方向上的m个值y(i)</param>/// <param name="z">一维数组,长度为n x m,存放给定的n x m个结点的函数值z(i,j),z(i,j) = f(x(i), y(j)), i=0,1,...,n-1, j=0,1,...,m-1</param>/// <param name="u">存放插值点x坐标</param>/// <param name="v">存放插值点y坐标</param>/// <returns>指定函数值f(u, v)</returns>public static double Lagrange_3Points_2D(double[] x, double[] y, double[] z, double u, double v){// x方向上给定结点的点数int n = x.Length;// y方向上给定结点的点数int m = y.Length;// 初值int nn = 3;// 特例int ip;if (n <= 3){ip = 0;nn = n;}else if (u <= x[1]){ip = 0;}else if (u >= x[n - 2]){ip = n - 3;}else{int i = 1;int j = n;while (((i - j) != 1) && ((i - j) != -1)){int w = (i + j) / 2;if (u < x[w - 1]){j = w;}else{i = w;}}if (Math.Abs(u - x[i - 1]) < Math.Abs(u - x[j - 1])){ip = i - 2;}else{ip = i - 1;}}int mm = 3;int iq;if (m <= 3){iq = 0;mm = m;}else if (v <= y[1]){iq = 0;}else if (v >= y[m - 2]){iq = m - 3;}else{int i = 1;int j = m;while (((i - j) != 1) && ((i - j) != -1)){int w = (i + j) / 2;if (v < y[w - 1]){j = w;}else{i = w;}}if (Math.Abs(v - y[i - 1]) < Math.Abs(v - y[j - 1])){iq = i - 2;}else{iq = i - 1;}}double[] b = new double[3];for (int i = 0; i <= nn - 1; i++){b[i] = 0.0;for (int j = 0; j <= mm - 1; j++){int k = m * (ip + i) + (iq + j);double h = z[k];for (k = 0; k <= mm - 1; k++){if (k != j){h = h * (v - y[iq + k]) / (y[iq + j] - y[iq + k]);}}b[i] = b[i] + h;}}double zv = 0.0;for (int i = 0; i <= nn - 1; i++){double h = b[i];for (int j = 0; j <= nn - 1; j++){if (j != i){h = h * (u - x[ip + j]) / (x[ip + i] - x[ip + j]);}}zv = zv + h;}return (zv);}}
}
POWER BY 315SOFT.COM
基于坐标点的计算,从点集计算插值曲线等拓展方法请参阅《拉格朗日插值算法及其拓展》
