容斥原理

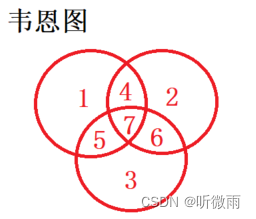
如上图所示：
∣s1∪s2∪s3∣=∣s1∣+∣s2∣+∣s3∣−∣s1∩s2∣−∣s1∩s3∣−∣s2∩s3∣+∣s1∩s2∩s3∣\\begin{aligned} |s_1 \\cup s_2 \\cup s_3|&=|s_1|+|s_2|+|s_3|-|s_1 \\cap s_2|-|s_1 \\cap s_3|-|s_2 \\cap s_3|+|s_1 \\cap s_2 \\cap s_3| \\end{aligned} ∣s1​∪s2​∪s3​∣​=∣s1​∣+∣s2​∣+∣s3​∣−∣s1​∩s2​∣−∣s1​∩s3​∣−∣s2​∩s3​∣+∣s1​∩s2​∩s3​∣​
时间复杂度：
Cn1+Cn2+Cn3+⋯+CnnC_n^1+C_n^2+C_n^3+\\cdots+C_n^nCn1​+Cn2​+Cn3​+⋯+Cnn​
因为Cn0+Cn1+Cn2+Cn3+⋯+Cnn=2nC_n^0+C_n^1+C_n^2+C_n^3+\\cdots+C_n^n=2^nCn0​+Cn1​+Cn2​+Cn3​+⋯+Cnn​=2n,等式的左右两边都是等于从n个中选任意多个数的方案，$2$表示第$i$个到底选不选的方案数，2n2^n2n就表示$n$个中选不选对应数的方案数。
所以Cn1+Cn2+Cn3+⋯+Cnn=2n−Cn0=2n−1C_n^1+C_n^2+C_n^3+\\cdots+C_n^n=2^n-C_n^0=2^n-1Cn1​+Cn2​+Cn3​+⋯+Cnn​=2n−Cn0​=2n−1

同理存在等式：Ck1−Ck2+Ck3−Ck4+⋯+(−1)k−1Ckk=1C_k^1-C_k^2+C_k^3-C_k^4+\\cdots+(-1)^{k-1}C_k^k=1Ck1​−Ck2​+Ck3​−Ck4​+⋯+(−1)k−1Ckk​=1
所以∣s1∪s2∪s3∣=∑i∣si∣−∑i⋅j∣si∩sj∣+∑ijk∣si∩sj∩sk∣−⋯|s_1\\cup s_2 \\cup s_3|=\\sum_i|s_i|-\\sum_{i \\cdot j}|s_i \\cap s_j|+\\sum_{ijk}|s_i\\cap s_j \\cap s_k|-\\cdots∣s1​∪s2​∪s3​∣=∑i​∣si​∣−∑i⋅j​∣si​∩sj​∣+∑ijk​∣si​∩sj​∩sk​∣−⋯

能被整除的数

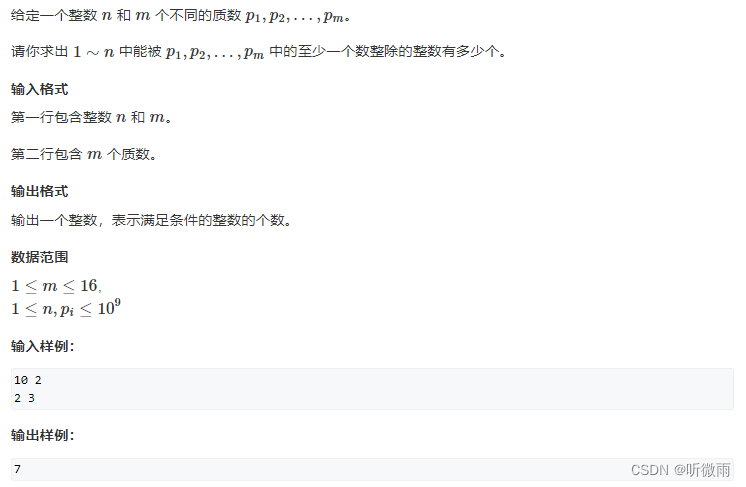
题解：

这里主要用二进制数表示某个数是否被选，1代表被选，0代表不被选，二进制中1的个数为奇数，说明为奇数个集合相交，前面的符号为+，反之为偶数个集合相交，前面的符号为-。

import java.io.*;public class Main{static int N=20;static int[] p=new int[N];public static void main(String[] args)throws IOException{BufferedReader in=new BufferedReader(new InputStreamReader(System.in));String[] strs=in.readLine().split(" ");int n=Integer.parseInt(strs[0]);int m=Integer.parseInt(strs[1]);strs=in.readLine().split(" ");for(int i=0;i<m;i++)p[i]=Integer.parseInt(strs[i]);int res=0;for(int i=1;i<(1<<m);i++){int t=1;int cnt=0;for(int j=0;j<m;j++){if((i>>j&1)==1){cnt++;if((long)t*p[j]>n){t=-1;break;}t=t*p[j];}}if(t!=-1){if(cnt%2==0)res-=n/t;else res+=n/t;}}System.out.println(res);}
}