【砝码称重】暴力DFS(一半分)+ dp(可AC)

题目描述:
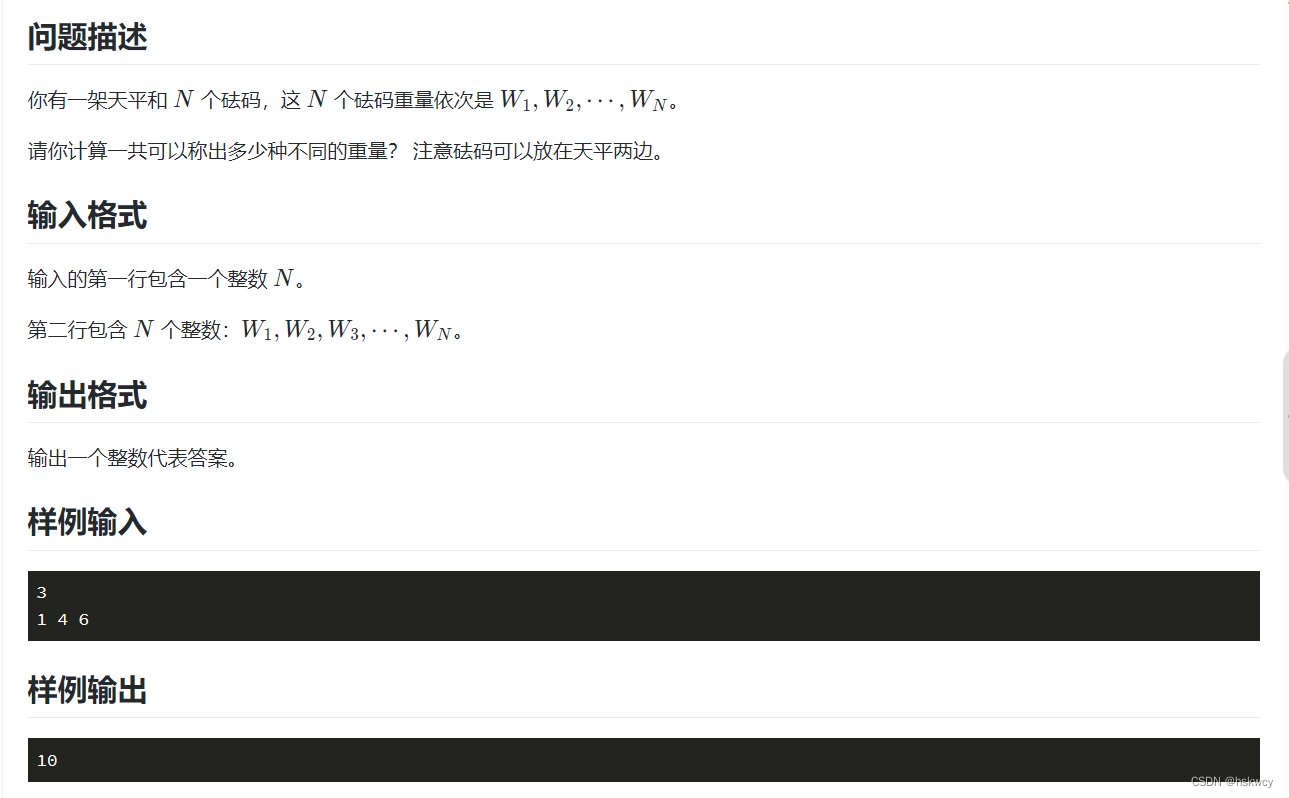
题目分析:

我也没有完全搞太明白,简单说说我的理解
1.dp【i】【j】表示前 i 个砝码,是否可以称出来重量为 j 的物品,如果可以的话,值为1,不可以
为0;
2.针对当前第 i 个砝码,一共有三种选择,分别是放到左边、右边又或者是不放该砝码【优先将砝码放在右边】
如题例所示:第一个砝码【重 1】可以称重 0 与 1 两个重量
此时开始处理第二个砝码,重 4 :
第一种:将砝码放在右边:那么右边砝码的重量就是 1 + 4 = 5;可以称出质量为 5 的物品,则dp【2】【5】= 1;
第二种:将砝码放在左边:那么右边砝码的重量就是 1 ,左边砝码质量为 4 ,可以称出质量为 3 的物品,则dp【2】【3】= 1;
第三种:不放砝码:可以称出质量为 1 的物品,则dp【2】【1】= 1;
但是如何用动态规划的思路将再这种思想用编程实现了:
首先,设定初始值当 0 个砝码时,只有 重量 0 可以被称出来,令dp【0】【0】= 1;其余值全部为0;
接下来:处理第一个砝码,依次判断dp【1】【j】的值,那怎么判断呢?
根据状态转移式: dp[i][j] = max(dp[i-1][j],max(dp[i-1][j+w[i]],dp[i-1][abs(j-w[i])]));
首先是dp【1】【0】= max(dp[0][0],max(dp[0][1],dp[0][1])) = 1;
解释:dp[0][0]:既然不放第 1 个物品,质量 0 就被称出来了,那么加上砝码 1 也可以称出来质量 0 ;dp[0][1]、dp[0][1]:表示前0个砝码的组合是否可以称出质量为4的物品。那肯定不可以,所以表达式dp【1】【0】的值就是1,表示前1个砝码可以称出体积为 0 的物品;
接下来判断dp【1】【1】:前前1个砝码可以称出体积为 1 的物品
dp【1】【1】= max(dp[0][1],max(dp[0][2],dp[0][0]))
解释:dp[0][1] = 0、dp[0][2] = 0【这个式子表示将第一个砝码放在右边的情况:只要这个dp[0][2] =1,说明可以称出来质量为2的物品,那么就能dp[1][1]也一定能成功,因为将该砝码放到左边,为了保持平衡,左边要再添加重量为 1 的物品,这样也就被称出来了】意思好像是:加在右边的话,是通过左边加物品实现平衡的
dp[0][0] = 1;【表示将砝码放在左边的情况】
再举个例子dp【3】【7】:
dp【2】【7】:
dp【2】【7 + 6】:如果为真,那就说明前两个砝码可以称出质量为13的物品,那么把该砝码放到天平左侧,为了保持平衡,左侧还需要添加质量为7的物品,那么质量为7的物品就被测量出来了
dp【2】【7 - 6】:如果为真,那就说明前两个砝码可以称出质量为1的物品,那么把该砝码放到天平右侧,为了保持平衡,左侧还需要添加质量为7的物品,那么质量为7的物品就被测量出来了
题解代码:
dsp:
//砝码称重--一半的分
#include <bits/stdc++.h>
using namespace std;
const int vinf = 1e5+100; //砝码之和最大
int vis[vinf]; //用来标记该质量是否可以被称重
int n;
int val[vinf];
void dfs(int x,int y)
{if(y==n+1){if(x>=0){vis[x]=1;cout<<x<<endl;} return;}//开始深搜dfs(x + val[y],y + 1); // 砝码放到左边 dfs(x - val[y],y + 1); //砝码放到右边 dfs(x,y+1);
}
int main(){cin>>n;//输入砝码的重量for(int i=1;i<=n;++i){//cin>>val[i]; //打印出可以撑出来的 }//已经读取了砝码的重量dfs(0,0); //初始状态左边为已经平衡的天平左边的重量,右边为第 i 个砝码//开始枚举每一个重量int ans = 0; for(int i=1;i<vinf;++i){if(vis[i]) ans++; }cout<<endl<<ans<<endl;return 0;
}dp:
//砝码称重--dp
#include <bits/stdc++.h>
using namespace std;
int n,w[110];
int dp[110][100005];
int ans = 0;
int main(){cin>>n;int sum=0;for(int i=1;i<=n;++i){cin>>w[i];sum+=w[i];}dp[0][0]=1;for(int i=1;i<=n;++i){for(int j=0;j<=sum;++j){dp[i][j] = max(dp[i-1][j],max(dp[i-1][j+w[i]],dp[i-1][abs(j-w[i])]));}}for(int i=1;i<=sum;++i){if(dp[n][i])ans++;}cout<<ans<<endl; return 0;
}

