堆数据结构

堆是一种特殊的基于树的数据结构,其中树是一棵完全二叉树。
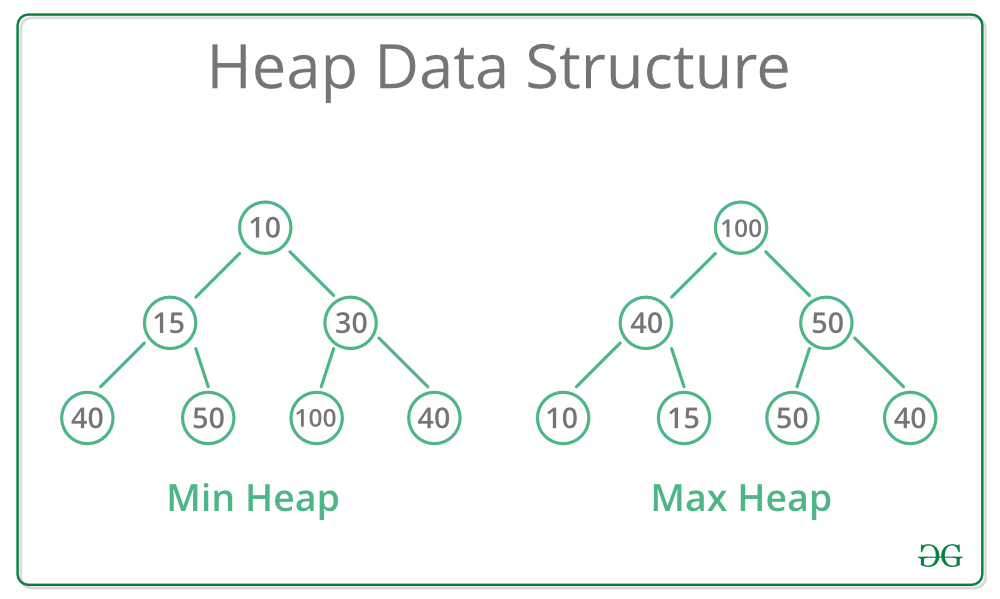
堆数据结构的操作:
- Heapify:从数组创建堆的过程。
- 插入:在现有堆中插入一个元素的过程,时间复杂度为 O(log N)。
- 删除:删除堆顶元素或优先级最高的元素,然后组织堆并返回时间复杂度为O(log N)的元素。
- Peek:检查或查找堆中最优先的元素(最大和最小堆的最大或最小元素)。
堆数据结构的类型
通常,堆可以有两种类型:
- Max-Heap:在 Max-Heap 中,出现在根节点的键必须是出现在它所有子节点的键中最大的。对于该二叉树中的所有子树,相同的属性必须递归地为真。
- Min-Heap:在 Min-Heap 中,出现在根节点的键必须是出现在它所有子节点的键中的最小值。对于该二叉树中的所有子树,相同的属性必须递归地为真。
二进制堆
二进制堆是最小堆或最大堆。在最小二进制堆中,根键必须是二进制堆中所有键中最小的键。对于二叉树中的所有节点,相同的属性必须递归为真。Max Binary Heap类似于MinHeap
最小堆的例子:
10 10
/ \\ / \\
20 100 15 30
/ / \\ / \\
30 40 50 100 40
二进制堆是如何表示的?
二叉堆是完全二叉树。二叉堆通常表示为数组。
- 根元素将位于 Arr[0]。
- 下表显示了第 i个节点的其他节点的索引,即 Arr[i]:
| Arr[(i-1)/2] | 返回父节点 |
| Arr(2*i)+1] | 返回左子节点 |
| Arr[(2*i)+2] | 返回右子节点 |
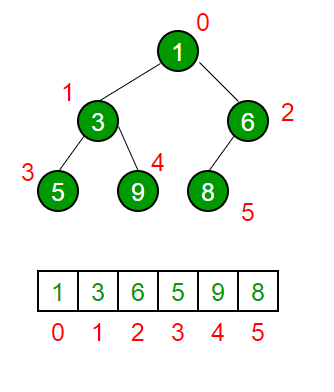
堆操作:
下面是基本堆操作的C代码实现.
// A C++ program to demonstrate common Binary Heap Operations
#include<iostream>
#include<climits>
using namespace std;// Prototype of a utility function to swap two integers
void swap(int *x, int *y);// A class for Min Heap
class MinHeap
{int *harr; // pointer to array of elements in heapint capacity; // maximum possible size of min heapint heap_size; // Current number of elements in min heap
public:// ConstructorMinHeap(int capacity);// to heapify a subtree with the root at given indexvoid MinHeapify(int );int parent(int i) { return (i-1)/2; }// to get index of left child of node at index iint left(int i) { return (2*i + 1); }// to get index of right child of node at index iint right(int i) { return (2*i + 2); }// to extract the root which is the minimum elementint extractMin();// Decreases key value of key at index i to new_valvoid decreaseKey(int i, int new_val);// Returns the minimum key (key at root) from min heapint getMin() { return harr[0]; }// Deletes a key stored at index ivoid deleteKey(int i);// Inserts a new key 'k'void insertKey(int k);
};// Constructor: Builds a heap from a given array a[] of given size
MinHeap::MinHeap(int cap)
{heap_size = 0;capacity = cap;harr = new int[cap];
}// Inserts a new key 'k'
void MinHeap::insertKey(int k)
{if (heap_size == capacity){cout << "\\nOverflow: Could not insertKey\\n";return;}// First insert the new key at the endheap_size++;int i = heap_size - 1;harr[i] = k;// Fix the min heap property if it is violatedwhile (i != 0 && harr[parent(i)] > harr[i]){swap(&harr[i], &harr[parent(i)]);i = parent(i);}
}// Decreases value of key at index 'i' to new_val. It is assumed that
// new_val is smaller than harr[i].
void MinHeap::decreaseKey(int i, int new_val)
{harr[i] = new_val;while (i != 0 && harr[parent(i)] > harr[i]){swap(&harr[i], &harr[parent(i)]);i = parent(i);}
}// Method to remove minimum element (or root) from min heap
int MinHeap::extractMin()
{if (heap_size <= 0)return INT_MAX;if (heap_size == 1){heap_size--;return harr[0];}// Store the minimum value, and remove it from heapint root = harr[0];harr[0] = harr[heap_size-1];heap_size--;MinHeapify(0);return root;
}// This function deletes key at index i. It first reduced value to minus
// infinite, then calls extractMin()
void MinHeap::deleteKey(int i)
{decreaseKey(i, INT_MIN);extractMin();
}// A recursive method to heapify a subtree with the root at given index
// This method assumes that the subtrees are already heapified
void MinHeap::MinHeapify(int i)
{int l = left(i);int r = right(i);int smallest = i;if (l < heap_size && harr[l] < harr[i])smallest = l;if (r < heap_size && harr[r] < harr[smallest])smallest = r;if (smallest != i){swap(&harr[i], &harr[smallest]);MinHeapify(smallest);}
}// A utility function to swap two elements
void swap(int *x, int *y)
{int temp = *x;*x = *y;*y = temp;
}// Driver program to test above functions
int main()
{MinHeap h(11);h.insertKey(3);h.insertKey(2);h.deleteKey(1);h.insertKey(15);h.insertKey(5);h.insertKey(4);h.insertKey(45);cout << h.extractMin() << " ";cout << h.getMin() << " ";h.decreaseKey(2, 1);cout << h.getMin();return 0;
}
输出
2 4 1
- getMin():它返回最小堆的根元素。此操作的时间复杂度为O(1)。在 maxheap 的情况下,它将是getMax()。
- extractMin():从 MinHeap 中移除最小元素。此操作的时间复杂度为O(log N) ,因为此操作需要在删除根后维护堆属性(通过调用heapify() )。
- decreaseKey():减少键的值。此操作的时间复杂度为O(log N)。如果一个节点的减少键值大于该节点的父节点,那么我们不需要做任何事情。否则,我们需要向上遍历来修复违反的堆属性。
- insert(): 插入一个新key需要O(log N)时间。我们在树的末尾添加一个新键。如果新的键比它的父键大,那么我们不需要做任何事情。否则,我们需要向上遍历以修复违反的堆属性。
- delete(): 删除ke也需要O(log N)时间。我们通过调用reducekey()将要删除的键替换为最小的无穷大。在reducekey()之后,负无穷值必须到达根,因此我们调用extractMin()来删除键。
