目录

58. 最后一个单词的长度 Length of Last Word  🌟

59. 螺旋矩阵 II Spiral Matrix II  🌟🌟

60. 排列序列 Permutation Sequence  🌟🌟🌟

🌟 每日一练刷题专栏 🌟

Golang每日一练 专栏

Python每日一练 专栏

C/C++每日一练 专栏

Java每日一练 专栏

58. 最后一个单词的长度 Length of Last Word

给你一个字符串 s，由若干单词组成，单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。

单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。

示例 1：

输入：s = "Hello World"
输出：5
解释：最后一个单词是“World”，长度为5。

示例 2：

输入：s = "   fly me   to   the moon  "
输出：4
解释：最后一个单词是“moon”，长度为4。

示例 3：

输入：s = "luffy is still joyboy"
输出：6
解释：最后一个单词是长度为6的“joyboy”。

提示：

• 1 <= s.length <= 10^4
• s 仅有英文字母和空格 ' ' 组成
• s 中至少存在一个单词

代码1：

使用strings.Split()：将字符串按照空格分割成多个子字符串，然后取最末的字符串长度即可。 

func lengthOfLastWord(s string) int {strs := strings.Split(s, " ")for i := len(strs) - 1; i >= 0; i-- {if len(strs[i]) > 0 {return len(strs[i])}}return 0
}

代码2：

反向遍历：从字符串末尾开始向前遍历，找到第一个不为空格的字符，然后再向前遍历，直到遇到空格或到达字符串开头为止，这段子字符串的长度即为最后一个单词的长度。

func lengthOfLastWord(s string) int {n := len(s)i := n - 1for i >= 0 && s[i] == ' ' {i--}if i < 0 {return 0}j := ifor j >= 0 && s[j] != ' ' {j--}return i - j
}

59. 螺旋矩阵 II Spiral Matrix II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。 

示例 1：

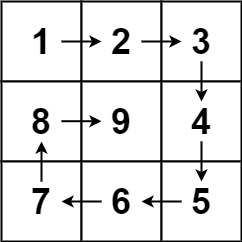
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 20

代码1：

按层模拟 按照从外到内的顺序，依次填入矩阵中的每一个元素。 

func generateMatrix(n int) [][]int {matrix := make([][]int, n)for i := range matrix {matrix[i] = make([]int, n)}num, left, right, top, bottom := 1, 0, n-1, 0, n-1for left <= right && top <= bottom {for i := left; i <= right; i++ {matrix[top][i] = numnum++}for i := top + 1; i <= bottom; i++ {matrix[i][right] = numnum++}if left < right && top < bottom {for i := right - 1; i > left; i-- {matrix[bottom][i] = numnum++}for i := bottom; i > top; i-- {matrix[i][left] = numnum++}}left++right--top++bottom--}return matrix
}

代码2：

模拟转圈 用四个变量分别记录当前填数位置所在的行列范围，然后按照“向右、向下、向左、向上”的顺序不断填入数值，每填入一个数就更新当前位置和范围。

func generateMatrix(n int) [][]int {matrix := make([][]int, n)for i := range matrix {matrix[i] = make([]int, n)}num, row, col, direction := 1, 0, 0, 0directions := [][]int{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}for num <= n*n {matrix[row][col] = numnum++nextRow, nextCol := row+directions[direction][0], col+directions[direction][1]if nextRow < 0 || nextRow >= n || nextCol < 0 || nextCol >= n || matrix[nextRow][nextCol] != 0 {direction = (direction + 1) % 4}row += directions[direction][0]col += directions[direction][1]}return matrix
}

60. 排列序列 Permutation Sequence

给出集合 [1,2,3,...,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

"123" "132" "213" "231" "312" "321"

给定 n 和 k，返回第 k 个排列。

示例 1：

输入：n = 3, k = 3
输出："213"

示例 2：

输入：n = 4, k = 9
输出："2314"

示例 3：

输入：n = 3, k = 1
输出："123"

提示：

• 1 <= n <= 9
• 1 <= k <= n!

代码1：

暴力枚举 生成第 k 个排列，可以先生成第一个排列，然后一直调用 next_permutation() 函数，直到生成第 k 个排列。

func getPermutation(n int, k int) string {nums := make([]int, n)for i := 0; i < n; i++ {nums[i] = i + 1}for i := 1; i < k; i++ {next_permutation(nums)}ans := ""for _, num := range nums {ans += strconv.Itoa(num)}return ans
}
func next_permutation(nums []int) {n := len(nums)i := n - 2for i >= 0 && nums[i] >= nums[i+1] {i--}if i < 0 {reverse(nums, 0, n-1)return}j := n - 1for j >= 0 && nums[j] <= nums[i] {j--}nums[i], nums[j] = nums[j], nums[i]reverse(nums, i+1, n-1)
}
func reverse(nums []int, left, right int) {for left < right {nums[left], nums[right] = nums[right], nums[left]left++right--}
}

代码2：

阶乘数组法 首先计算出第一个排列，然后找到第 k 个排列与第一个排列的差距，根据差距计算出第 k 个排列。 首先可以计算出第一个排列。对于一个长度为 n 的排列，第 i 个位置上的数字可以取 {1,2,...,n-i+1} 中的任意一个，因此第一个排列可以计算出来。 接下来计算第 k 个排列相对于第一个排列的差距。对于第一个位置，有 n 种选择，因此第 k 个排列的第一个数字就是第 k/(n-1)!+1 (向上取整) 小的数字。然后将这个数字从候选数字中删除，继续计算第二个数字。以此类推，就可以计算出第 k 个排列。 

func getPermutation(n int, k int) string {factorials := make([]int, n+1)factorials[0] = 1for i := 1; i <= n; i++ {factorials[i] = factorials[i-1] * i}nums := make([]int, n)for i := 0; i < n; i++ {nums[i] = i + 1}k--ans := ""for i := n - 1; i >= 0; i-- {index := k / factorials[i]ans += strconv.Itoa(nums[index])nums = append(nums[:index], nums[index+1:]...)k -= index * factorials[i]}return ans
}

代码3： 回溯法

func getPermutation(n int, k int) string {nums := make([]int, n)for i := 0; i < n; i++ {nums[i] = i + 1}res := ""backtrack(&nums, k-1, &res)return res
}func backtrack(nums *[]int, k int, res *string) {if len(*nums) == 0 {return}n := len(*nums)factorial := 1for i := 2; i < n; i++ {factorial *= i}index := k / factorial*res += strconv.Itoa((*nums)[index])*nums = append((*nums)[:index], (*nums)[index+1:]...)k %= factorialbacktrack(nums, k, res)
}

🌟 每日一练刷题专栏 🌟

✨ 持续，努力奋斗做强刷题搬运工！

👍 点赞，你的认可是我坚持的动力！ 

🌟 收藏，你的青睐是我努力的方向！ 

✎ 评论，你的意见是我进步的财富！  

☸ 主页：https://hannyang.blog.csdn.net/ 

	Golang每日一练 专栏
	Python每日一练 专栏
	C/C++每日一练 专栏
	Java每日一练 专栏