二项式反演

在很多情况下，“恰好”往往是不好求的，因为恰好意味着"$\le$"并且"$\ge$"，需要进行很多限制，破坏了情况之间的独立性。

二项式反演则通过一定手段，使得限制"$\le$"与"$\ge$"中只保留一个，使得情况独立，便于处理。

二项式定理：

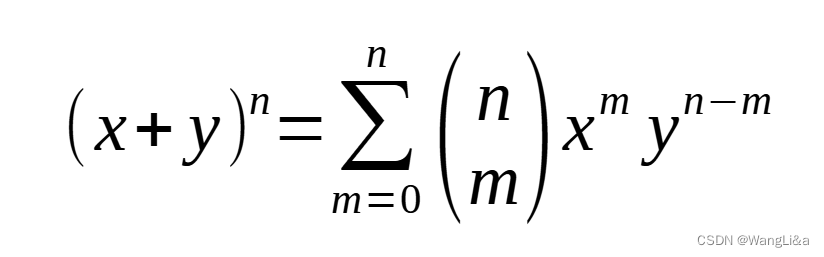
推论：

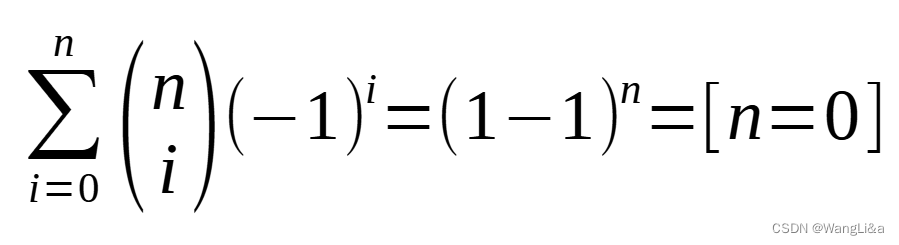
二项式反演公式：

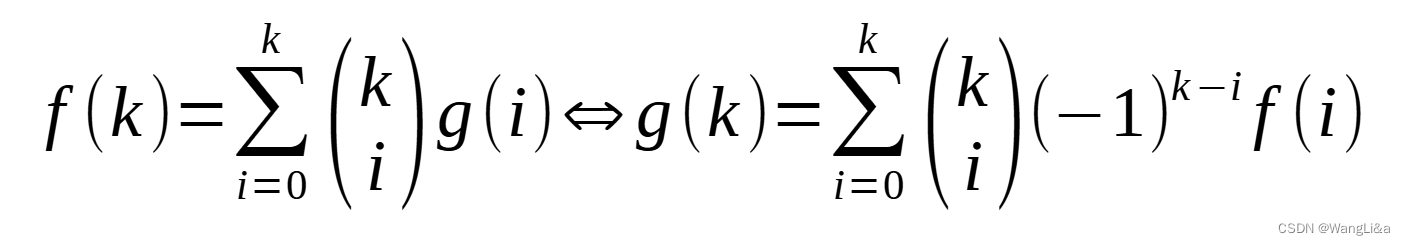
证明一下：
只证明左边到右边。仿照证明过程容易证明右边到左边。

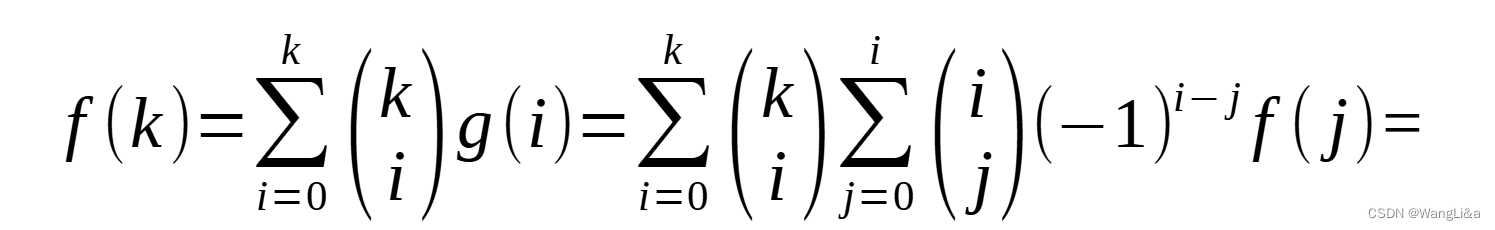
注意到若$j>i$，则(ji)=0(^i_j)=0(ji​)=0，可扩大枚举范围：

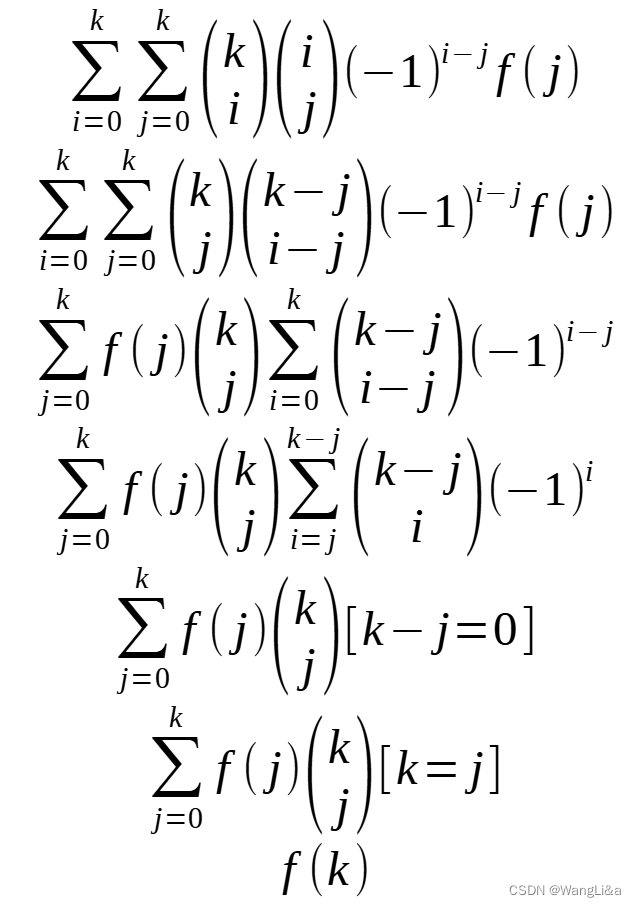
当然这里有一个非常有意思的地方就是，一些地方的证明中有如下过程：
∑i=0k∑j=0i=∑j=0k∑i=0j\\overset{k}{\\underset {i=0}\\sum}\\overset{i}{\\underset {j=0}\\sum}=\\overset{k}{\\underset {j=0}\\sum}\\overset{j}{\\underset {i=0}\\sum}i=0∑​k​j=0∑​i​=j=0∑​k​i=0∑​j​

这是在描述，把被和式求值的部分看做一个三角矩阵，左边是先对行求和，右边是先对列求和。

QED.

恰好->至多型

若对于一个问题，其限制条件为简单的数字形式，但是其细分是本质不同的，例如“恰好有两组成功配对的方案数”、“恰好有3人收到了礼物”，则这个条件可以根据加法细分。例如“两组”可以分为一组（A，B）、两组（AB），3人可以分为1人（A，B，C）、2人（AB，BC，AC）、3人（ABC）。

设$g(k)$表示恰好满足条件的方案数，$f(k)$表示至多满足条件的方案数，其中需要$f$是好求的。

则广泛存在一种关系：

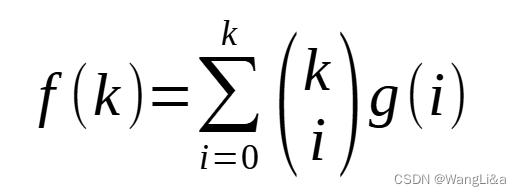
这是由于，对于$g(i)$而言，由于条件k是可分的，只需要从条件$k$中分出$i$份，就可以使得条件满足，而由于分出来的条件是本质不同的（例如满足收礼物是一个人，但收到礼物的可以是A，B或者C），因此一个$g(i)$对$f(k)$贡献的次数就是(ki)\\begin{pmatrix}k\\\\ i\\end{pmatrix}(ki​)。

则可以反演求出$g$：

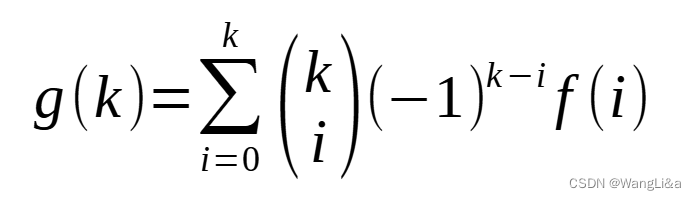
因此两类二项式反演都要满足两个条件：

• 限制条件可分
• 分为相同值的限制条件本质不同

错位排列

设$f(i)$表示至多有i个位置排错的方案数，$g(i)$表示恰好有i个位置排错的方案数。

显然“i”可分，有n个位置，就会有n-1个位置，n-2个位置…，显然分出来的"位置"本质不同，例如两个位置，可以是前两个位置，也可以是第1、第3个位置。

则有：

因而有：

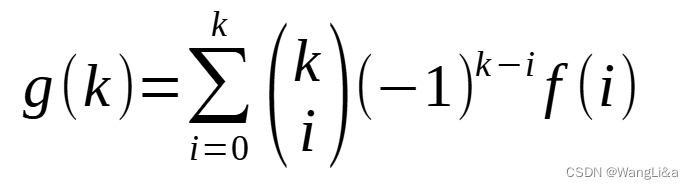
注意到$f(i)$是非常好求的，因为至多有$i$个位置排错就相当于全排列。即$f(i)=i!$

因此就可以了。

#include<iostream>
using namespace std;
long long p[25];
int n;
int main() {p[0]=1;for(int i=1;i<=20;i++) p[i]=p[i-1]*i;cin>>n;long long ans=0;for(int i=0;i<=n;i++)ans+=p[n]/p[i]*(i&1?-1:1);cout<<ans;return 0;
}
实现上对式子做了一些变换

UVALive 7040

题意简述，有一排n个格子，m种颜色，涂满颜色，使得相邻格子颜色不同，并且每一种颜色都（都就是恰好嘛）用到，统计方案数。
（1≤n≤109,1≤m≤1061\\leq n\\leq 10^9,1\\leq m\\leq 10^61≤n≤109,1≤m≤106）

每一种颜色都用到，显然是很不好求的。一种显然的做法是首先强制每种颜色用一次，然后把这些强制的位置插进格子里，做全排列，不过显然这样会有重复情况，所以这种做法假了，所以我们用二项式反演让它变得好求。

设$f(i)$表示至多用i种颜色的方案数，$g(i)$表示恰好用i种颜色的方案数。
显然"i种颜色"可分，显然分的"颜色"本质不同，比如两种颜色，可以是红蓝，也可以是绿蓝、黄蓝。

我们注意到，根据组合容易求出f(i)=i(i−1)n−1f(i)=i(i-1)^{n-1}f(i)=i(i−1)n−1。反演求出$g$即可。

分特产

题目所说同一种的特产是无标号的，人是有标号的。

显然“每个人至少一件”是非常不好求的，因为这样每种特产之间就不独立了。我们先考虑可以 有人 没有，这样就不会互相影响了。

可以 有人 没有的方案数是非常好求的，设目前有$i$个人，特产用$a$表示，则方案数就是：

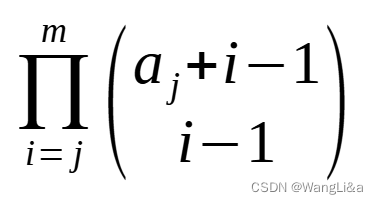
这是因为，我们意识到每一种特产之间是相互独立的，考虑第$j$种特产分为$i$份，就相当于把aja_jaj​个相同元素放到$i$个可空集合的方案数，对应方程∑k=1ixk=aj\\overset{i}{\\underset{k=1}\\sum}x_k=a_jk=1∑​i​xk​=aj​的非负整数解的个数。

设$f(i)$表示至多有$i$个人分到至少一份特产的方案数，$g(i)$为恰好有$i$个人分到至少一份的方案数。
则可以反演。

#include<iostream>
using namespace std;
const int N=1000;
const long long M=1e9+7;
long long a[N+5],C[2*N+5][2*N+5],f[N+5],g[N+5];
int n,m;
int main() {cin>>n>>m;for(int i=1;i<=m;i++) cin>>a[i];for(int i=0;i<=N;i++) C[i][0]=1;for(int i=1;i<=2*N;i++)for(int j=1;j<=i;j++)(C[i][j]=C[i-1][j-1]+C[i-1][j])%=M;for(int i=1;i<=n;i++)f[i]=1;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)(f[i]*=C[a[j]+i-1][i-1])%=M;
//	for(int i=0;i<=n;i++)
//		cout<<i<<':'<<f[i]<<endl;for(int i=0;i<=n;i++)(g[n]+=C[n][i]*f[i]*((n-i)&1?-1:1))%=M;cout<<(g[n]%M+M)%M;		
}注意到这里g只用到一项，但是为了视觉效果就不改了。

恰好->至少型（指定答案型）

设$g(k)$表示恰好满足条件$k$的方案数，$f(k)$表示至少满足条件$k$的方案数，或者说指定$k$个位置，使得其满足条件，剩下的位置则不做限制，可以满足条件，也可以不满足。

因此有：

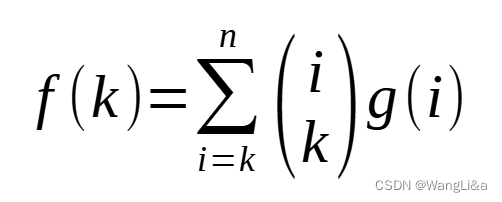
其中n表示问题的极大上界，也可以说，使得$i>n,g(i)=0,即g(i)无意义$。

这个公式就是说说，对于满足$i$个情况来说，只需要从其中任取满足情况的$i$个中的$k$个，即可符合$f(k)$的要求，因此在$f(k)$中被贡献了(ik)\\begin{pmatrix}i\\\\ k\\end{pmatrix}(ik​)次。

具体来说，总共有3个人，设$f(1)$表示至少有一个人收到礼物的情况数，我们可以枚举这个人是A,B或C，则ABC都收到礼物的情况，就被统计了三次，AB,BC,AC收到礼物的情况，分别被统计了两次。

则有：

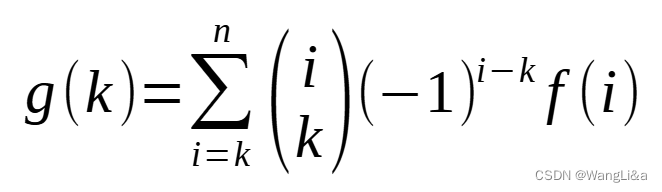
判定条件也是那两点，对于“i个人”收到礼物而言，i是可分的，而人是有标号的，就满足条件，存在$f$与$g$的二项式反演关系式。

BZOJ2839 集合取数

题意简述：
一个有n个不同元素的集合有2ⁿ个不同子集，现在其子集中取出至少一个集合，使得其交集的元素个数恰好为k，求合法方案数。
（1≤n≤106,0≤k≤n1\\leq n\\leq 10^6,0\\leq k\\leq n1≤n≤106,0≤k≤n）

我们注意到，设$f(i)$表示交集大小至少为i的方案数，则这是非常好求的，f(i)=(ni)(22n−i−1)f(i)=\\begin{pmatrix}n\\\\ i\\end{pmatrix}\\left(2^{2^{n-i}}-1\\right)f(i)=(ni​)(22n−i−1)。这是因为，含有$i$个元素的情形有(ni)\\begin{pmatrix}n\\\\ i\\end{pmatrix}(ni​)种，则含有这i个元素的集合有2n−i2^{n-i}2n−i个，每个集合可选可不选，但不能都不选。

我们设$g(i)$表示交集大小恰好为$i$（也就是有i个交集）的方案数，则我们注意到，i可分，并且交集之间两两不同，也就是有标号，因此构成二项式反演关系。

较为复杂的二项式反演

记题目中的k为K。设糖果为a，药片为b。
我们称ai>bja_i>b_jai​>bj​为合法情况。

首先注意到若n+K为奇数，则无解。（方案数是0）

然后对于K是偶数的情况，注意到题目中有“恰好”这个意思，因此考虑二项式反演。

设$f(i)$表示至少有$i$组a>b的情况数，$g(i)$表示恰好有$i$组a>b的情况数。注意到i是可分的（有i组合法的情况，就会有i-1组合法的情况），并且情况数相同的时候，情况是有不同的，因此可以二项式反演。

接下来求$f(i)$，需要一个简单dp的过程，首先把a、b数组升序排序，然后设Fi,jF_{i,j}Fi,j​表示前i个a，与全部的b做匹配，至少 j组合法情况的方案数。

首先有不知道是合法还是不合法的匹配，Fi,j+=Fi,j−1F_{i,j}+=F_{i,j-1}Fi,j​+=Fi,j−1​，合法更好，不合法拉倒。换句话说，搁置aia_iai​，aia_iai​先不做匹配，等dp到n的位置，确定完了所有合法匹配之后，再做随机匹配。

其次有合法匹配，记b数组中小于aia_iai​的有k个，Fi,j+=Fi−1,j−1×(k−(j−1))F_{i,j}+=F_{i-1,j-1}\\times (k-(j-1))Fi,j​+=Fi−1,j−1​×(k−(j−1))。这是因为对于aia_iai​而言的合法匹配的区域必然包含原有合法匹配的区域，不能占以前的位置，因此要减去j-1。

考虑边界条件，显然Fi,0=1F_{i,0}=1Fi,0​=1，这并不是说有0组合法情况的方案数一定只有一种，而是说当从Fi,0F_{i,0}Fi,0​处转移时，理应获得1的贡献。也可以说我们搁置了a1,...,aia_1,...,a_ia1​,...,ai​的所有位置，等到dp到n的时候再随机匹配。

注意到f(i)=(n−i)!Fn,if(i)=(n-i)!F_{n,i}f(i)=(n−i)!Fn,i​，因为有i对合法匹配，剩下的位置被搁置了，随机匹配。

就做完了。

#include<iostream>
#include<algorithm>
using namespace std;
const int N=2000;
const long long M=1e9+9;
int n,K;
long long p[N+5],C[N+5][N+5];
long long f[N+5],F[N+5][N+5];
int a[N+5],b[N+5];
int main() {cin>>n>>K;if((n+K)&1) {cout<<0;return 0;}for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) cin>>b[i];for(int i=0;i<=N;i++) C[i][0]=1;for(int i=1;i<=N;i++)for(int j=1;j<=i;j++)(C[i][j]=C[i-1][j-1]+C[i-1][j])%=M;sort(a+1,a+1+n);sort(b+1,b+1+n);for(int i=0;i<=n;i++) F[i][0]=1;
//	cout<<"*";for(int i=1;i<=n;i++) {long long k=upper_bound(b+1,b+1+n,a[i])-b;
//		cout<<k<<' ';for(int j=1;j<=i;j++) (F[i][j]+=F[i-1][j]+F[i-1][j-1]*max((long long)k-j,0ll))%=M;}
//	for(int i=1;i<=n;i++,cout<<endl)
//		for(int j=1;j<=i;j++)
//			cout<<F[i][j]<<' '; 
//	cout<<"*";p[0]=1;for(long long i=1;i<=N;i++)(p[i]=i*p[i-1])%=M;for(int i=0;i<=n;i++)(f[i]=F[n][i]*p[n-i])%=M;K=n+K>>1;long long g=0;for(int i=K;i<=n;i++)(((g+=C[i][K]*f[i]*(i-K&1?-1:1))%=M)+=M)%=M;cout<<g;
}

后记

于是皆大欢喜。