目录

题目要求：给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

方法一：递归

方法二：迭代

思路分析：

复杂度分析

代码展示：

方法三：Morris 遍历

思路分析：

复杂度分析

代码展示：

题目要求：给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

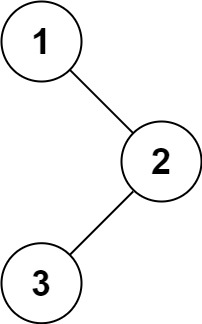
输入：root = [1,null,2,3]
输出：[1,3,2]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

 

方法一：递归

递归的方法和二叉树的前序遍历在之前的博客中已经写过，需要的小伙伴可以点击链接查看

递归求二叉树的前中后序遍历

【LeetCode】二叉树的前序遍历（递归，迭代，Morris遍历）

这篇文章主要来讲解非递归的方法对二叉树进行中序遍历

方法二：迭代

思路分析：

迭代的方式其实与递归是等价的，区别在于递归的时候隐式地维护了一个栈，而我们在迭代的时候

需要显式地将这个栈模拟出来，其余的实现与细节都相同，具体可以参考下面的代码

复杂度分析

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为迭代过程中显式栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)

代码展示：

 public List<Integer> inorderTraversal(TreeNode root) {List <Integer> list = new ArrayList<>();Stack <TreeNode> stack = new Stack<>();//栈非空或者root非空while(root != null || !stack.isEmpty()){//先根后左入栈while(root != null){stack.push(root);root = root.left;}//此时root为空，说明上一个入栈的root没有左子树//没有左子树，可以出栈root = stack.pop();list.add(root.val);//此时判断右子树root = root.right;}return list;}

方法三：Morris 遍历

Morris 遍历使用二叉树节点中大量指向 null 的指针，由 Joseph Morris 于 1979 年发明。

思路分析：

将当前根节点的左侧最右侧节点的right指向当前根节点，省去了栈的维护，连接之后可以直接顺着节点遍历完整个二叉树，以下图为例：

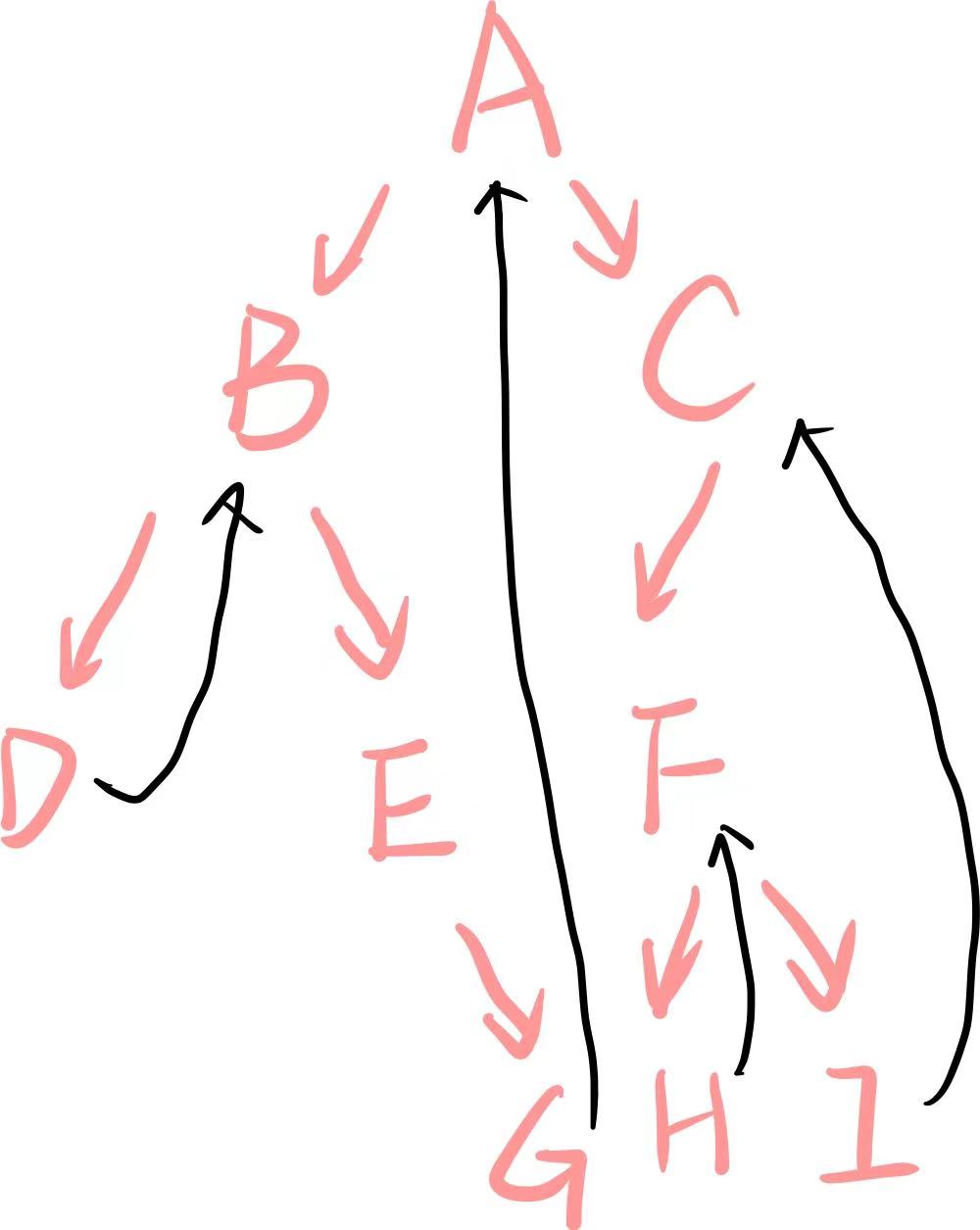
复杂度分析

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(1)

代码展示：

    public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if(root == null){return list;}TreeNode cur1 = root;TreeNode cur2 = null;while(cur1 != null){cur2 = cur1.left;if(cur2 != null){while(cur2.right != null && cur2.right != cur1){cur2 = cur2.right;}//此时说明cur2走向了最右侧子树//1.还未连接，建立连接if(cur2.right != cur1){cur2.right = cur1;cur1 = cur1.left;continue;//否则说明已经走过，断开连接}else{cur2.right = null;list.add(cur1.val);}}else{list.add(cur1.val);}cur1 = cur1.right;}return list;}