浅谈字符串问题

字符串同余
我们定义 字符串的模运算 : TmodPT \\bmod PTmodP 结果为 TTT 的最长后缀 , 且同时为 PPP 的最长前缀.
例如 P=abaP=\\text{aba}P=aba
amodP=a\\text{a} \\bmod P = \\text{a}amodP=a
bmodP=∅\\text{b} \\bmod P = \\emptybmodP=∅
abmodP=ab\\text{ab} \\bmod P = \\text{ab}abmodP=ab
bamodP=∅\\text{ba} \\bmod P = \\emptybamodP=∅
baamodP=a\\text{baa} \\bmod P = \\text{a}baamodP=a
abamodP=aba\\text{aba} \\bmod P = \\text{aba}abamodP=aba
⋯\\cdots⋯
若 TmodPT \\bmod PTmodP 等于 PPP 本身 , 则 PPP 在 TTT 末尾处出现一次.
根据定义, 我们可以得出以下性质:
记 aaa 是一个字符 , SSS 是一个字符串 , PPP 给定.
-
aaa 拼在 SSS 前面 :
aSmodP={aSSmodPaS \\bmod P= \\begin{cases} aS\\\\ S \\bmod P \\end{cases}aSmodP={aSSmodP
-
aaa 拼在 SSS 后面 :
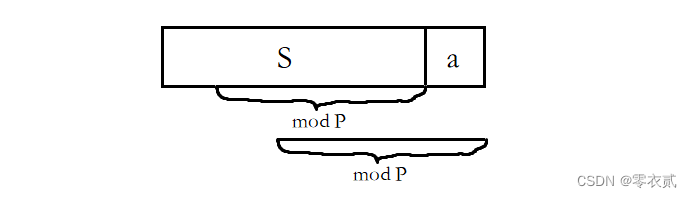
SamodP=((SmodP)+a)modPSa \\bmod P= ((S \\bmod P) + a ) \\bmod PSamodP=((SmodP)+a)modP
( +++ 也表示拼接)
考虑到对 PPP 取模后结果是 PPP 的前缀 , 我们也可以用数字表示对 PPP 取模后的前缀长度. 如 kkk 就表示 P[0...k)P[0...k)P[0...k).
现我们已知一个字符串 TTT , TmodP=kT \\bmod P =kTmodP=k 和一个字符 ccc, 我们想知道 TcmodPTc \\bmod PTcmodP 的结果.
TcmodP=((TmodP)+c)modPTc \\bmod P = ((T \\bmod P) + c) \\bmod PTcmodP=((TmodP)+c)modP (性质 2)
=(P[0...k)+c)modP=(P[0...k)+c) \\bmod P=(P[0...k)+c)modP
-
定义函数 go(k,c)\\text{go(k,c)}go(k,c) 来求解 (P[0...k)+c)modP(P[0...k)+c) \\bmod P(P[0...k)+c)modP.
-
定义 f(k)f(k)f(k) 表示 P[1...k)modPP[1...k) \\bmod PP[1...k)modP 的结果. 即 P[1...k)modPP[1...k) \\bmod PP[1...k)modP 等于 P[0...f(k))P[0...f(k))P[0...f(k)). 容易发现 , 因为 P[1...k)P[1...k)P[1...k) 只有 k−1k-1k−1 位 , 所以f(k)f(k)f(k) 严格小于 kkk.
对于 go(k,c)\\text{go(k,c)}go(k,c) , 分几种情况:
-
P[0...k)+c=P[k](P[k]=c)P[0...k)+c=P[k] \\qquad (P[k]=c)P[0...k)+c=P[k](P[k]=c)
答案为 P[0...k]P[0...k]P[0...k] , 即 P[0...k+1)P[0...k+1)P[0...k+1) , 即前缀长度为 k+1k+1k+1 .
-
P[0]P[0]P[0] 对于运算是多余的 (结合上述图片理解)
那么答案为 (P[1...k)+c)modP(P[1...k)+c) \\bmod P(P[1...k)+c)modP , 也就是 (P[0...f(k))+c)modP(P[0...f(k)) + c) \\bmod P(P[0...f(k))+c)modP , 即 go(f(k),c)\\text{go(f(k),c)}go(f(k),c). 而 f(k)<kf(k)<kf(k)<k , 相当于是去求解一个子问题.
找出 patternpatternpattern 在 texttexttext 中出现的位置
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e6 + 5;
string text, pattern;
int f[MAXN];
int go(int k, char c)
{if(pattern[k] == c) return k + 1;else if(k > 0) return go(f[k], c);else return 0;
}
int main()
{cin >> text >> pattern; f[1] = 0; // P[1,1) mod P == 0for(int i=1; i<pattern.size(); i++)f[i + 1] = go(f[i], pattern[i]);int res = 0;for(int i=0; i<text.size(); i++){res = go(res, text[i]);if(res == pattern.size()) cout << i << "\\n";}return 0;
}例题1 : 无限猴子
题目
记 E(S)E(S)E(S) 表示当前字符串为 SSS , 停止时长度的期望.
若 P=101P=101P=101
E(∅)=12E(0)+12E(1)+1E(\\empty) = \\frac 1 2 E(0) + \\frac 1 2 E(1) +1E(∅)=21E(0)+21E(1)+1
E(1)=12E(10)+12E(11)+1E(1) = \\frac 1 2 E(10) + \\frac 1 2 E(11) + 1E(1)=21E(10)+21E(11)+1
E(10)=12E(100)+12E(101)+1E(10) = \\frac 1 2 E(100) + \\frac 1 2 E(101) + 1E(10)=21E(100)+21E(101)+1
E(101)=0E(101) = 0E(101)=0
…
这样显然应该有无限项 , 但如果字符串 A,BA,BA,B 满足 A≡B(modP)A \\equiv B \\pmod PA≡B(modP) , 有 E(A)=E(B)E(A)=E(B)E(A)=E(B) , 因此我们只关注字符串 SmodPS\\bmod PSmodP 后的结果.
记 E(S)E(S)E(S) 表示当前字符串 modP\\bmod PmodP 结果为 SSS , 停止时长度的期望.
那么便只有:
E(∅)=12E(∅)+12E(1)+1E(\\empty) = \\frac 1 2 E(\\empty) + \\frac 1 2 E(1) +1E(∅)=21E(∅)+21E(1)+1
E(1)=12E(10)+12E(1)+1E(1) = \\frac 1 2 E(10) + \\frac 1 2 E(1) + 1E(1)=21E(10)+21E(1)+1
E(10)=12E(∅)+12E(101)+1E(10) = \\frac 1 2 E(\\empty) + \\frac 1 2 E(101) + 1E(10)=21E(∅)+21E(101)+1
E(101)=0E(101) = 0E(101)=0
用数字表示前缀,同时将式子左右同乘以 222 :
2E(0)=E(0)+E(1)+22E(0) = E(0) + E(1) + 22E(0)=E(0)+E(1)+2
2E(1)=E(2)+E(1)+22E(1) = E(2) + E(1) + 22E(1)=E(2)+E(1)+2
2E(2)=E(0)+E(3)+22E(2) = E(0) + E(3) + 22E(2)=E(0)+E(3)+2
E(3)=0E(3) = 0E(3)=0
写成一般形式 : 2E(i)=E(i+1)+E(gi)+22E(i)=E(i+1) + E(g_i)+22E(i)=E(i+1)+E(gi)+2
其中 gig_igi 表示 (P[0...i)+c)modP(P[0...i)+c )\\bmod P(P[0...i)+c)modP , 其中 ccc 为 Pi‾\\overline{P_i}Pi (PiP_iPi 取反), 即 gi=go(i,Pi‾)g_i=go(i, \\overline{P_i})gi=go(i,Pi)
由第一个式子,我们可以将 E(1)E(1)E(1) 表示为 a1×E(0)+b1a_1\\times E(0)+b_1a1×E(0)+b1
以此类推 , 将 E(i)E(i)E(i) 表示为 ai×E(0)+bia_i \\times E(0) + b_iai×E(0)+bi :
2E(i)=E(i+1)+E(gi)+22E(i)=E(i+1) + E(g_i)+22E(i)=E(i+1)+E(gi)+2
E(i+1)=2E(i)−E(gi)−2E(i + 1) = 2 E(i) - E(g_i) - 2E(i+1)=2E(i)−E(gi)−2
ai+1×E(0)+bi+1=(2ai−agi)∗E(0)+(2bi−bgi−2)a_{i+1} \\times E(0) + b_{i+1} = (2a_i - a_{g_i}) * E(0) + (2b_i - b_{g_i} - 2)ai+1×E(0)+bi+1=(2ai−agi)∗E(0)+(2bi−bgi−2)
得 ai+1=2ai−agi,bi+1=2bi−bgi−2a_{i+1}=2a_i - a_{g_i}, b_{i+1}=2b_i - b_{g_i} - 2ai+1=2ai−agi,bi+1=2bi−bgi−2
由于 E(0)=E(0)E(0) = E(0)E(0)=E(0) , 即 a0=1a_0=1a0=1 , 剩下的 ai+1=2ai−agia_{i+1}=2a_i - a_{g_i}ai+1=2ai−agi 类推均为 111 , 得 aaa 永远为 111.
最终带入 E(n)=an×E(0)+bn=E(0)+bn=0E(n)=a_n \\times E(0) + b_n=E(0)+b_n=0E(n)=an×E(0)+bn=E(0)+bn=0 , 求解 E(0)=−bnE(0)=-b_nE(0)=−bn .
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 5e5 + 5;
const int mod = 1e9 + 7;
int n, p[MAXN], f[MAXN], g[MAXN], a[MAXN], b[MAXN];
int go(int k, int c)
{if(p[k] == c) return k + 1;else if(k > 0) return go(f[k], c);else return 0;
}
signed main()
{cin >> n;for(int i=0; i<n; i++){char c; cin >> c;p[i] = c - '0';}f[1] = 0;for(int i=1; i<n; i++)f[i + 1] = go(f[i], p[i]);for(int i=0; i<n; i++)g[i] = go(i, p[i] ^ 1);for(int i=0; i<n; i++)b[i + 1] = ( 2 * b[i] - b[g[i]] - 2 ) % mod;cout << ( -b[n] + mod ) % mod;return 0;
}例题2 : 清除模式
题目
首先介绍暴力算法:before 表示已经处理完的,after 表示待处理的.
#include<bits/stdc++.h>
using namespace std;
string pattern, text;
int dfs(string before, string after)
{if(before.size() >= pattern.size())if(before.substr(before.size() - pattern.size()) == pattern) return 1e9;if(after == "") return 0;int r1 = dfs(before + after[0], after.substr(1));int r2 = dfs(before, after.substr(1)) + 1;return min(r1, r2);
}
int main()
{cin >> pattern >> text;cout << dfs("", text);return 0;
}记 after’ 为 after 串开始的位置:
#include<bits/stdc++.h>
using namespace std;
string pattern, text;
int dfs(string before, int after)
{if(before.size() >= pattern.size())if(before.substr(before.size() - pattern.size()) == pattern) return 1e9;if(after == text.size()) return 0;char c = text[after];int r1 = dfs(before + c, after + 1);int r2 = dfs(before, after + 1) + 1;return min(r1, r2);
}
int main()
{cin >> pattern >> text;cout << dfs("", 0);return 0;
}记 before’ 为 before 串 modP\\bmod PmodP 的结果
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e4 + 5;
string pattern, text;
int f[MAXN];
int go(int k, char c)
{if(pattern[k] == c) return k + 1;else if(k > 0) return go(f[k], c);else return 0;
}
int dfs(int before, int after)
{if(before == pattern.size()) return 1e9;if(after == text.size()) return 0;char c = text[after];int r1 = dfs(go(before, c), after + 1);int r2 = dfs(before, after + 1) + 1;return min(r1, r2);
}
int main()
{cin >> pattern >> text;for(int i=1; i<pattern.size(); i++)f[i+1] = go(f[i], pattern[i]);cout << dfs(0, 0);return 0;
}加上记忆化搜索:
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e4 + 5;
const int MAXM = 5005;
string pattern, text;
int f[MAXN];
int go(int k, char c)
{if(pattern[k] == c) return k + 1;else if(k > 0) return go(f[k], c);else return 0;
}
bool mem[MAXM][MAXN];
int cache[MAXM][MAXN];
int dfs(int before, int after)
{if(before == pattern.size()) return 1e9;if(after == text.size()) return 0;if(mem[before][after]) return cache[before][after];mem[before][after] = true;char c = text[after];int r1 = dfs(go(before, c), after + 1);int r2 = dfs(before, after + 1) + 1;return cache[before][after] = min(r1, r2);
}
int main()
{cin >> pattern >> text;for(int i=1; i<pattern.size(); i++)f[i+1] = go(f[i], pattern[i]);cout << dfs(0, 0);return 0;
}此时 , 还有一个点超时 , 原因为 gogogo 函数并非 O(1)O(1)O(1) , 考虑预处理出所有 gogogo 函数的值.
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e4 + 5;
const int MAXM = 5005;
string pattern, text;
int f[MAXN], g[MAXM][26];
int go(int k, char c)
{if(pattern[k] == c) return k + 1;else if(k > 0) return go(f[k], c);else return 0;
}
bool mem[MAXM][MAXN];
int cache[MAXM][MAXN];
int dfs(int before, int after)
{if(before == pattern.size()) return 1e9;if(after == text.size()) return 0;if(mem[before][after]) return cache[before][after];mem[before][after] = true;int c = text[after] - 'a';int r1 = dfs(g[before][c], after + 1);int r2 = dfs(before, after + 1) + 1;return cache[before][after] = min(r1, r2);
}
int main()
{cin >> pattern >> text;for(int i=1; i<pattern.size(); i++)f[i+1] = go(f[i], pattern[i]);for(int c=0; c<26; c++)for(int i=0; i<pattern.size(); i++)g[i][c] = go(i, c + 'a');cout << dfs(0, 0);return 0;
}