算法训练营第五十九天|LeetCode647、516

题目连接：647. 回文子串 - 力扣（LeetCode）

个人思路：dp数组的含义是：dp[i][j]：s字符串下标i到下标j的字串是否是一个回文串

这里我出现了错误

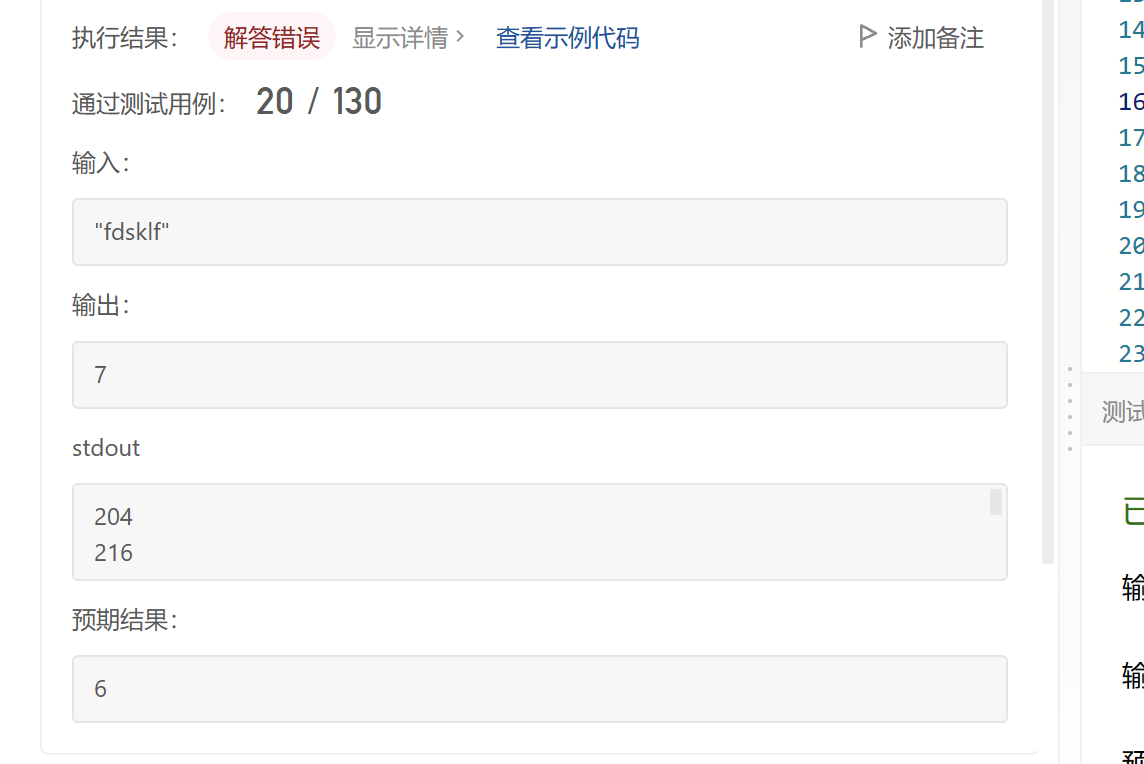
为什么出错呢？代码如下：

class Solution {public int countSubstrings(String s) {boolean[][] dp = new boolean[s.length()][s.length()];int result =0 ;for(int i=s.length()-1;i>=0;i--){for(int j=i;j<s.length();j++){if(s.charAt(i)==s.charAt(j)){System.out.println(s.charAt(i)+s.charAt(j));if(i-j<=1){dp[i][j] = true;result++;}else if(dp[i+1][j-1]){result++;dp[i][j] = true;                        }}}}return result;}
}

我错把j-i写成了i-j，因为j是不断往上加的，所以到了最后两端的时候，j肯定比i大，这个时候i-j就肯定是负数，那么结果就会误加1，这就是我错误的由来

还有一个错误是数组越界

class Solution {public int countSubstrings(String s) {boolean[][] dp = new boolean[s.length()][s.length()];int result =0 ;for(int i=s.length()-1;i>=0;i--){for(int j=0;j<s.length();j++){if(s.charAt(i)==s.charAt(j)){System.out.println(s.charAt(i)+s.charAt(j));if(i-j<=1){dp[i][j] = true;result++;}else if(dp[i+1][j-1]){result++;dp[i][j] = true;}}}}return result;}
}

我错误的把j初始化成0，而且j-i也写成了i-j，i-j为什么会数组越界呢？理由是此时i-j>1那么就会触发这个代码

因为j初始化为0，所以j-1必然-1因此报错

然后j不能初始化成0的原因是会造成重复

代码

class Solution {public int countSubstrings(String s) {boolean[][] dp = new boolean[s.length()][s.length()];int result =0;for(int i=s.length()-1;i>=0;i--){for(int j=i;j<s.length();j++){if(s.charAt(i)==s.charAt(j)){if(j-i<=1){dp[i][j] = true;result++;}else if(dp[i+1][j-1]){result++;dp[i][j] = true;                }}}}return result;}
}

题目链接：516. 最长回文子序列 - 力扣（LeetCode）

个人思路：这道题也简单，dp数组的含义是字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。

初始化是基于递推公式推导的，如果循环到两个最外层字符相等时，那么dp[i][j] = dp[i+1][j-1]+2;

如果不相等，那么就考虑取i到j-1的范围或者i+1到j的范围，从中选择最大值。

此外，两个指针遍历的过程中，会指向相同元素，这是递推公式所没有考虑到的，因此当指向相同元素的时候，也就是指向了一个元素，那么单个元素的最长回文子序列是1，因此使用for循环初始化成1

代码

class Solution {public int longestPalindromeSubseq(String s) {int[][] dp = new int[s.length()][s.length()];for(int i=0;i<s.length();i++){dp[i][i] = 1;}for(int i=s.length()-1;i>=0;i--){for(int j = i+1;j<s.length();j++){if(s.charAt(i)==s.charAt(j)){dp[i][j] = dp[i+1][j-1]+2;}else{dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);}}}int res = 0;for(int i=0;i<s.length();i++){for(int j=0;j<s.length();j++){res = Math.max(dp[i][j],res);}}return res;}
}