实验04:图像压缩(DP算法)

1.实验目的:
掌握动态规划算法的基本思想以及用它解决问题的一般技巧。运用所熟悉的编程工具,运用动态规划的思想来求解图像压缩问题。
2.实验内容:
给定一幅图像,求解最佳压缩,使得压缩后的文件最小。
3.实验要求:
实现lena512.raw(称为原文件)图像压缩并保存到文件(称为压缩文件)中。编写相应的解码器,对保存的文件解压出图像,并将解压图像存储为raw文件,通过图像浏览工具验证解压文件和原文件相同。分析压缩率(即 压缩文件大小 除以 原文件大小),分析算法的时间复杂度和空间复杂度。
□ \\square □ 基础性实验 □ \\square □ 综合性实验 ⊠ \\boxtimes ⊠ 设计性实验
实验报告正文
一、问题分析(模型、算法设计和正确性证明等)
设灰度图像共 n n n个像素值,灰度图像可以视作一个一维向量 P = { p 1 , p 2 , . . . . . . , p n } P=\\{p_1, p_2, ...... , p_n\\} P={p1,p2,......,pn},将n个像素分割成m个连续段 { S i } i = 1 m \\{S_i\\}_{i=1}^m {Si}i=1m.
其中,对第 i i i段 S i S_i Si有下列相关变量:
| 符号 | 表示含义 |
|---|---|
| l [ i ] l[i] l[i] | 段长,该段内包含像素个数 |
| b [ i ] b[i] b[i] | 该段中各像素位宽, b [ i ] = ⌈ log ( 1 + max p k ∈ S i p k ) ⌉ b[i]=\\lceil {\\log{(1+\\max_{p_k \\in S_i}{p_k}})} \\rceil b[i]=⌈log(1+maxpk∈Sipk)⌉ |
约定每段长度 l [ i ] l[i] l[i]满足:$1\\leq l[i] \\leq 256 且 且 且b[i]\\geq 1$.
已知: 0 ≤ p k ≤ 255 0\\leq p_k \\leq 255 0≤pk≤255,故 1 ≤ b [ i ] ≤ 8 1\\leq b[i]\\leq 8 1≤b[i]≤8
将 S i S_i Si编码压缩如下:
l [ i ] − 1 b [ i ] − 1 { p i + 1 , p i + 2 . . . . . . , p i + l [ i ] } 8 b i t s 3 b i t s l [ i ] × b [ i ] b i t s \\begin{matrix} l[i]-1 & b[i]-1 & \\{p_{i+1}, p_{i+2}......, p_{i+l[i]}\\}\\\\ 8bits & 3bits & l[i]\\times b[i]bits \\end{matrix} l[i]−18bitsb[i]−13bits{pi+1,pi+2......,pi+l[i]}l[i]×b[i]bits
压缩完成后,共占用空间: l [ i ] × b [ i ] + 11 l[i]\\times b[i] + 11 l[i]×b[i]+11
设 f ( { S i } 1 m ) f(\\{S_i\\}_1^m) f({Si}1m)表示压缩为 m m m个连续子段集合 { S i } 1 m \\{S_i\\}_1^m {Si}1m占用空间,则递归表达如下:
f ( { S i } 1 m ) = f ( { S i } 1 m − 1 ) + 11 (1) f(\\{S_i\\}_1^m)=f(\\{S_i\\}_1^{m-1})+11\\tag1 f({Si}1m)=f({Si}1m−1)+11(1)
最优子结构性质
设最优分段为 { S i } i = 1 m \\{S_i\\}_{i=1}^m {Si}i=1m,其中第 m m m个分段 S m S_m Sm的长度为 l e n len len,则 { S i } i = 1 m − 1 \\{S_i\\}_{i=1}^{m-1} {Si}i=1m−1是子问题 { p 1 , p 2 , . . . . . . , p n − l e n } \\{p_1, p_2, ......, p_{n-len}\\} {p1,p2,......,pn−len}的最优分段,递归表达如下:
f ( { S i } i = 1 m ) = f ( { S i } i = 1 m − 1 ) + f ( { S m } ) (2) f(\\{S_i\\}_{i=1}^m)=f(\\{S_i\\}_{i=1}^{m-1})+f(\\{S_m\\})\\tag2 f({Si}i=1m)=f({Si}i=1m−1)+f({Sm})(2)
简要证明过程如下:
假设 { S i } i = 1 m \\{S_i\\}_{i=1}^m {Si}i=1m为原问题最优分段,即 f ( { S i } i = 1 m ) f(\\{S_i\\}_{i=1}^m) f({Si}i=1m)值最小,但 { S i } i = 1 m − 1 \\{S_i\\}_{i=1}^{m-1} {Si}i=1m−1不是子问题的最优解。
则将其分段策略调整为最优解后, f ( { S i } i = 1 m − 1 ) f(\\{S_i\\}_{i=1}^{m-1}) f({Si}i=1m−1)值减少, f ( { S i } i = 1 m ) = f ( { S i } i = 1 m − 1 ) + f ( { S m } ) f(\\{S_i\\}_{i=1}^m)=f(\\{S_i\\}_{i=1}^{m-1})+f(\\{S_m\\}) f({Si}i=1m)=f({Si}i=1m−1)+f({Sm})值减少,与假设矛盾。
令g(n)表示像素序列{p_1, p_2, …, p_n}的最优分段占用空间,则有递归公式如下:
g ( n ) = min ( g ( n − k ) + k × b m a x + 11 ) , 1 ≤ k ≤ min ( n , 256 ) (3) g(n)=\\min(g(n-k)+k\\times b_{max}+11), 1\\leq k \\leq \\min{(n, 256)}\\tag3 g(n)=min(g(n−k)+k×bmax+11),1≤k≤min(n,256)(3)
二、算法设计复杂度分析(伪代码,不要粘贴源码)

时间复杂度:
T ( n ) ∈ θ ( ∑ i = 1 n min ( i , L m a x ) ) = θ ( L m a x × n ) = θ ( n ) T(n) \\in \\theta(\\sum_{i=1}^{n}{\\min{(i, Lmax)}})=\\theta(Lmax\\times n)=\\theta(n) T(n)∈θ(i=1∑nmin(i,Lmax))=θ(Lmax×n)=θ(n)
空间复杂度:
该算法需要辅助空间储存段长、位宽及前 i i i个像素最优压缩占用空间大小, S ( n ) ∈ θ ( n ) S(n)\\in \\theta(n) S(n)∈θ(n).
三、实验结果记录和分析(测试向量上的测试结果、运行时间)
实验结果:
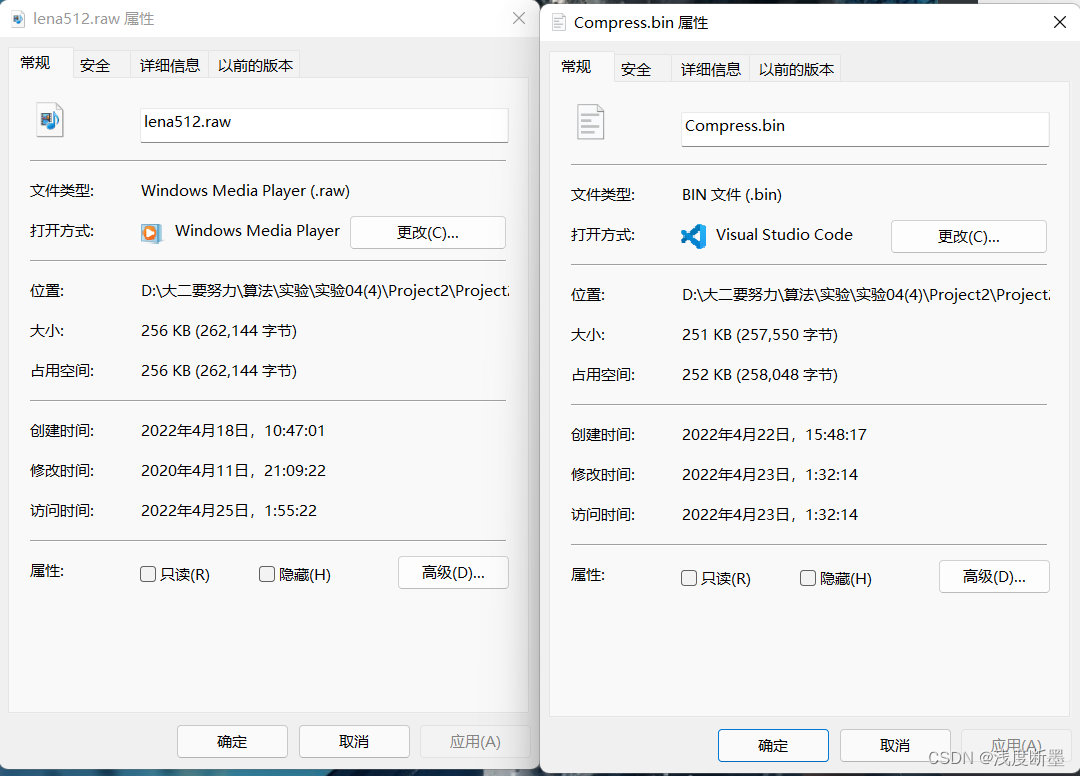
| 原图像大小 | 压缩后大小 |
|---|---|
| 262114字节 | 257550字节 |
压缩率: ( 1 − 257550 262114 ) × 100 % ≈ 1.75 % (1-\\frac{257550}{262114} )\\times 100\\% \\approx 1.75\\% (1−262114257550)×100%≈1.75%,详见RESULT文件夹
算法运行时间:267.847
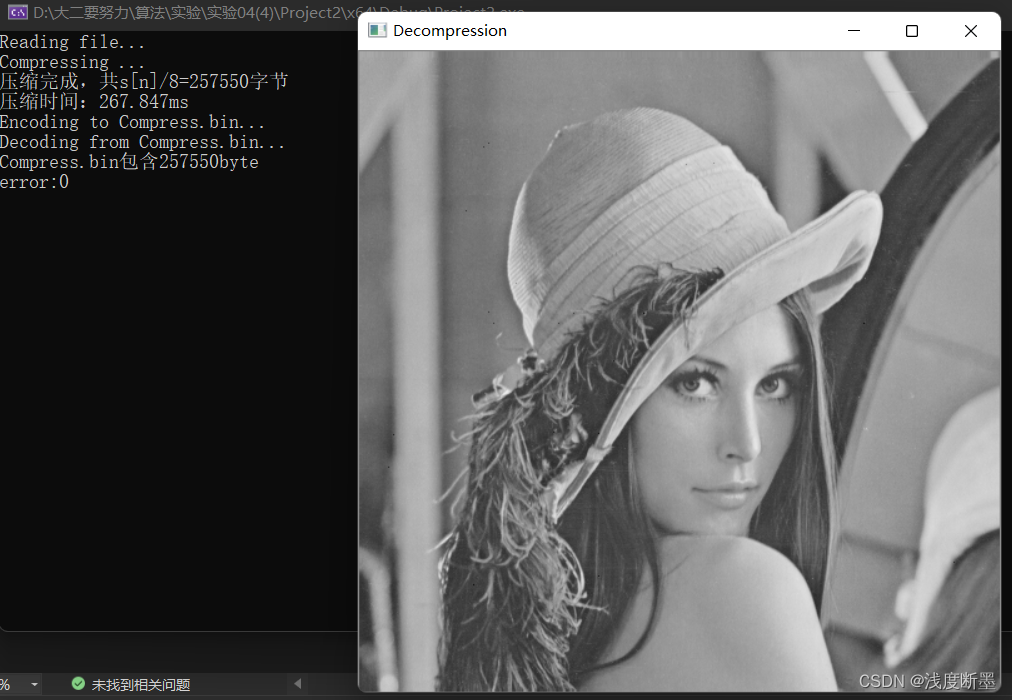
结果验证:
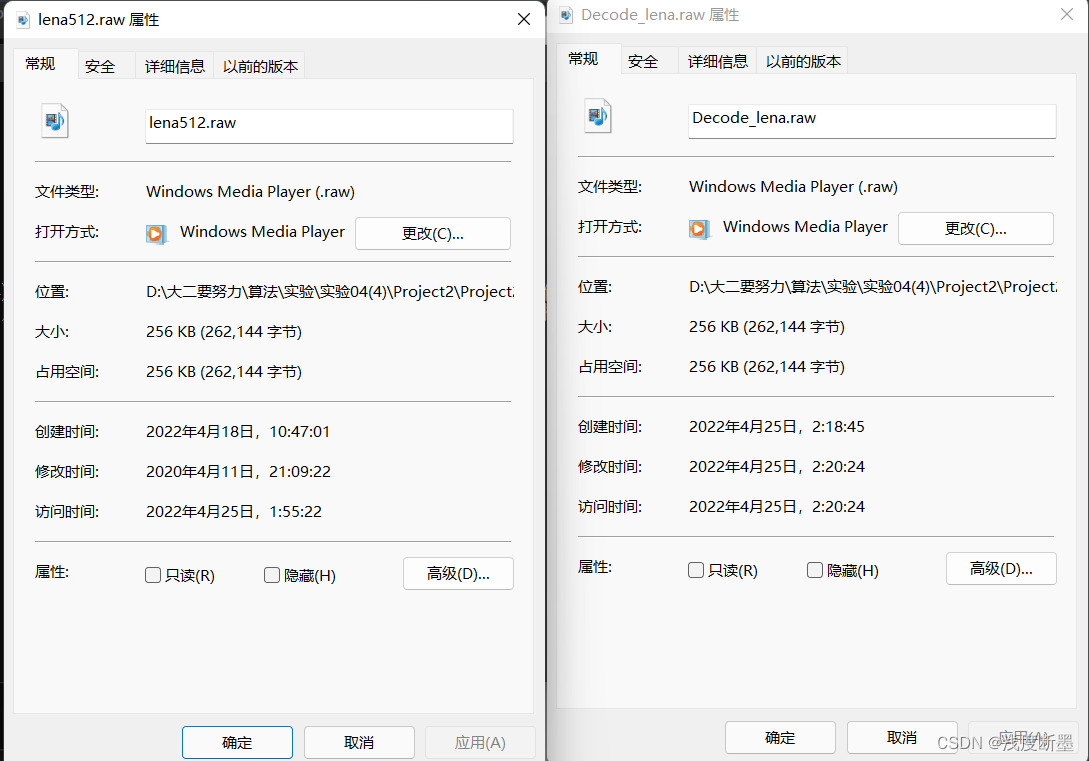
文件大小一致,下使用c++库OpenCV将Decode_lena.raw转存为jpg格式文件,详见RESULT文件夹。
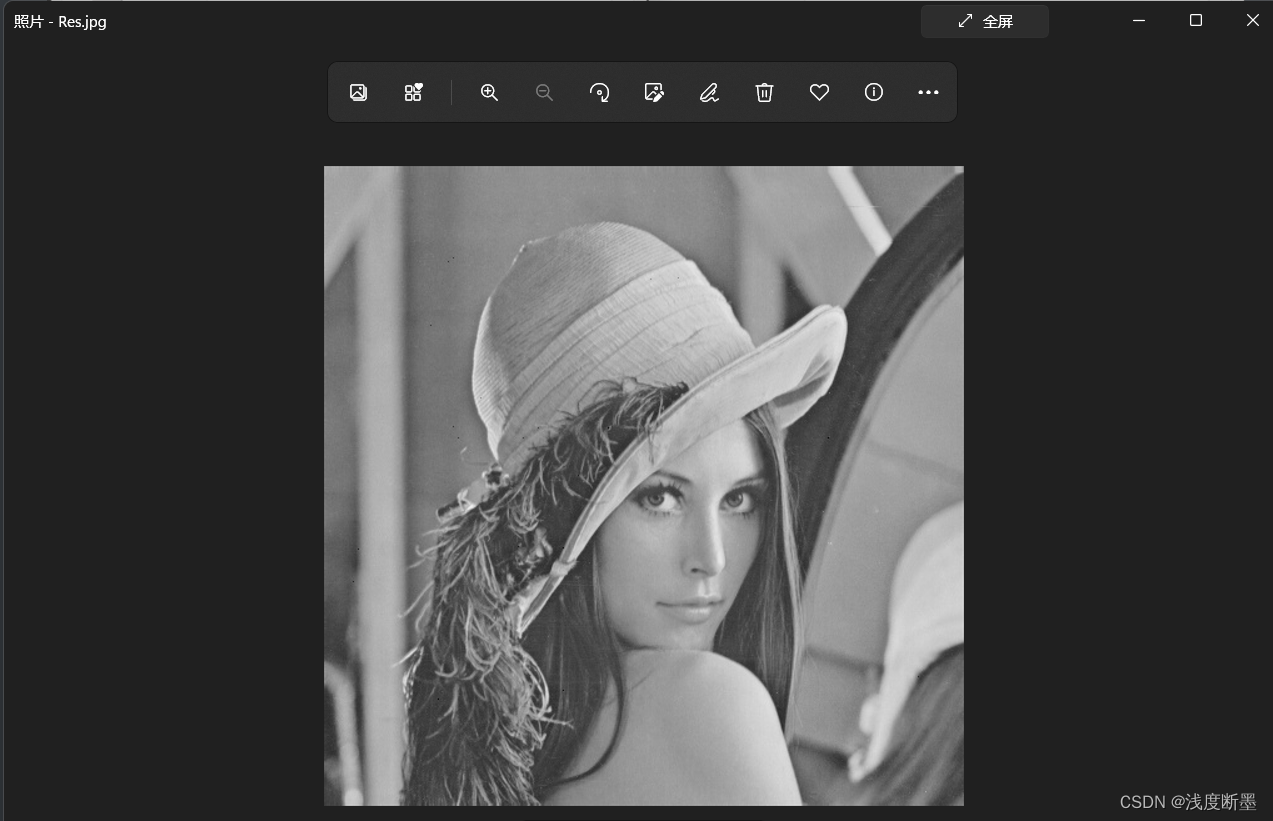
与原图像一致,详见RESULT文件夹。
四、总结(可描述出现的问题和解决方法、经验和反思等)
本实验中采用bin文件格式保存中间编码(压缩)文件以直观显示压缩完成后文件大小,本实验所有代码保存于CODE文件夹,所有结果保存于RESULT文件夹以便老师查阅。
本实验的压缩方式相对单一,压缩率较低,有较大提升空间,具体算法有:
- 将像素值均大于 2 7 = 128 2^7=128 27=128的分段进行取反操作,保存像素值与 256 256 256之差,段长最大值减一,需多加一位符号位表示是否取反,对于像素值较大的图像压缩率较大。
- 对于一段像素值用高斯分布等概率模型拟合,保存参数后解压时用概率分布函数生成像素值。
