Halo，这里是Ppeua。平时主要更新C语言，C++，数据结构算法......感兴趣就关注我吧！你定不会失望。

🌈个人主页：主页链接

🌈算法专栏：专栏链接

     我会一直往里填充内容哒！

🌈LeetCode专栏：专栏链接 

    目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目，也会当天做完发出

🌈代码仓库：Gitee链接

🌈点击关注=收获更多优质内容🌈

目录

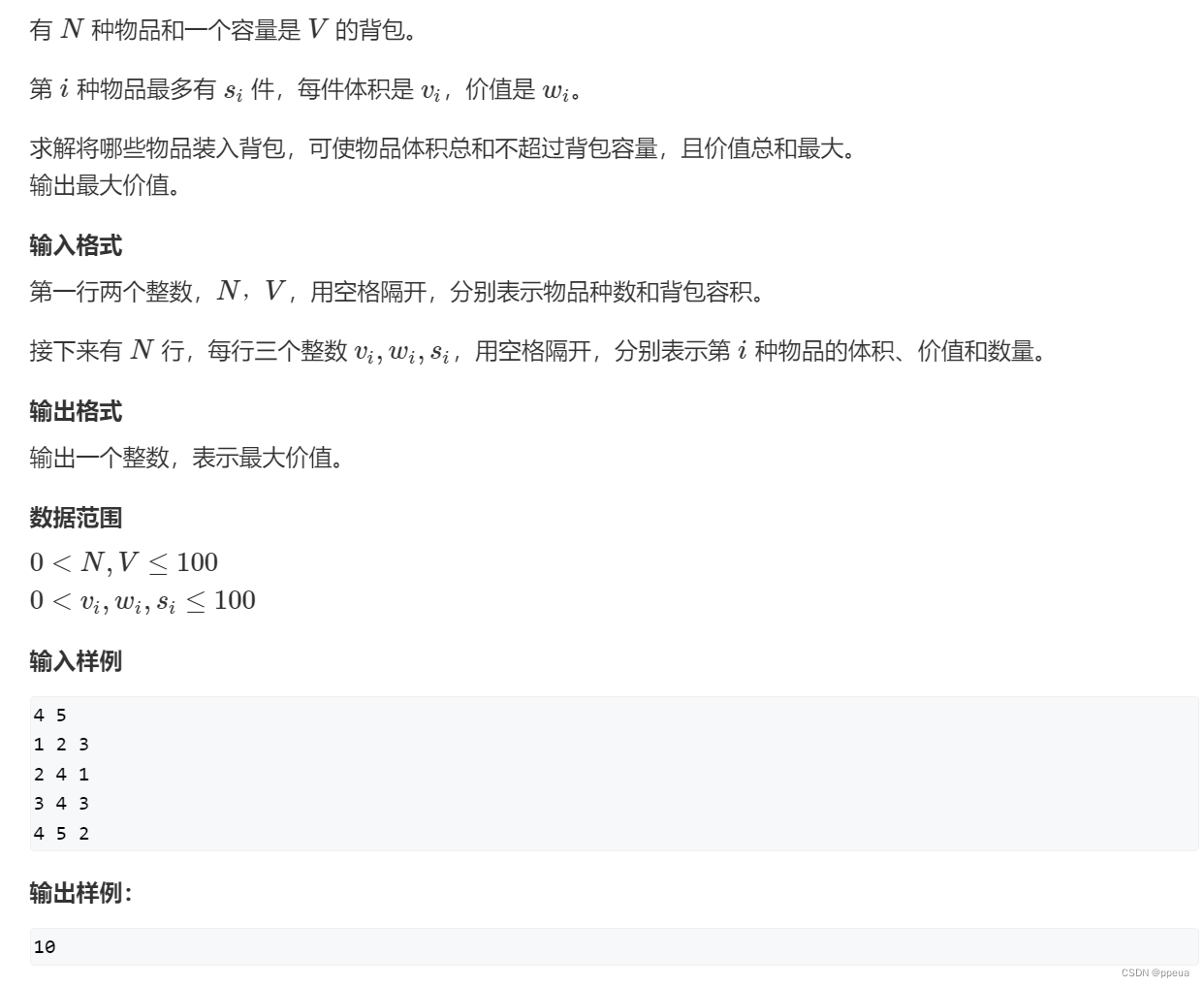
题目:多重背包问题

题解:

代码实现:

 优化：

代码实现:

题目:分组背包问题

 题解：

代码实现:

完结撒花：

题目:多重背包问题

题解:

与完全背包问题不同的是，每种东西都是有限件，前两种状态就不再过多赘述，有疑问的uu们可以去看看这篇文章完全背包，第三种状态我们直接枚举即可：当能拿下k个物品时，与不拿k件物品去最大值。

代码实现:

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1100;
int v[N],s[N],w[N],f[N][N];int main()
{int n=0,V=0;cin>>n>>V;for(int i=1;i<=n;i++){cin>>v[i]>>w[i]>>s[i];}for(int i=1;i<=n;i++){for(int j=1;j<=V;j++){for(int k=0;k*v[i]<=j&&k<=s[i];k++)f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+w[i]*k);}}cout<<f[n][V];
}

 优化：

这种做法虽然简单易懂，但时间复杂度为n^3，很容易就TLE了，所以我们必须优化一下。

这里有利用了一下快速幂（背增）的思想，不知道的uu们听我细说：

任何一个正整数都可以由二进制来表示（废话，那么我们要取得价值是不是也可以由二进制表示呢？

例如 我们有 1 2 4价值得东西，那我们就可以由这三个东西凑出0~7之间任何一个数

（由3个物品的表示凑出了7个情况），效率就高了

假设我们要凑0~9的任何一个数呢，那么1 2 4就无法表示了，我们可以给这区间加上一个2，是不是就可以表示0~9之间的任何一个情况了呢。

换到这题来看，数量为s的物品可以拆分为log s 个东西，就可以枚举出s个物品的情况，对应的价值乘上倍数k即可满足上面所说情况，所以对应的问题就变成了01背包问题

代码实现:

#include<iostream>
#include<algorithm>
using namespace std;
const int N=110000000;
int v[N],s[N],w[N],f[N][N];int solution2()
{int n=0,V=0;cin>>n>>V;int cnt=0;int k=1;for(int i=1;i<=n;i++){int a=0,b=0,s=0;cin>>a>>b>>s;int k=1;while(k<=s){v[++cnt]=a*k;w[cnt]=b*k;   s-=k;k*=2;}if(s>0){v[++cnt]=s*a;w[cnt]=s*b;}}n=cnt;for(int i=1;i<=n;i++){for(int j=V;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);}cout<<f[V];
}

题目:分组背包问题

 题解：

这题与完全背包问题也十分的相似，就是将一件物品无限拿，变成了一组物品挑一个。

代码实现:

#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int v[N][N],w[N][N],s[N],f[N];
int main()
{int n=0,m=0;cin>>n>>m;for(int i=1;i<=n;i++){cin>>s[i];for(int j=0;j<s[i];j++){cin>>v[i][j];cin>>w[i][j];}}for(int i=1;i<=n;i++){for(int j=m;j>=0;j--){for(int k=0;k<s[i];k++){if(j>=v[i][k])f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);}}}cout<<f[m];
}

完结撒花：

🌈本篇博客的内容【动态规划：多重背包问题，分组背包问题】已经结束。

🌈若对你有些许帮助，可以点赞、关注、评论支持下博主，你的支持将是我前进路上最大的动力。

🌈若以上内容有任何问题，欢迎在评论区指出。若对以上内容有任何不解，都可私信评论询问。

🌈诸君，山顶见！