学习目标：

我会采取以下几个步骤来学习插值多项式的求法：

1. 学习预备知识：插值多项式的求法需要掌握一定的数学知识，例如多项式函数的定义、导数、微积分、线性代数等等。因此，学习插值多项式的求法前，需要先学习相关的预备知识。

2. 研究插值多项式的定义和性质：插值多项式的求法是建立在插值多项式的定义和性质之上的。因此，学习插值多项式的求法时，需要深入了解插值多项式的定义、性质和应用。

3. 学习插值多项式的求法：插值多项式的求法有很多种，例如拉格朗日插值、牛顿插值、埃尔米特插值等等。需要系统地学习这些求法的步骤和原理，以及它们的优缺点和适用范围。

4. 实践练习：学习插值多项式的求法需要不断的实践练习。可以通过做数学练习题、模拟实验和编程实现来巩固和应用所学知识，以便更好地掌握插值多项式的求法。

5. 向专家请教：如果在学习过程中遇到了困难或者有疑问，可以向数学专家请教。他们可以帮助你解答问题，指导你的学习和实践，以便更好地掌握插值多项式的求法。

  2.1 拉格朗日插值多项式

拉格朗日插值多项式是一种常用的插值多项式，用于通过一组已知数据点 (x_i, y_i) 来构造一个多项式函数，使得该函数能够在这些数据点上完全符合原函数的形态。这种插值方法通常用于数据分析、信号处理、数值计算等地方。

拉格朗日插值多项式的公式为：

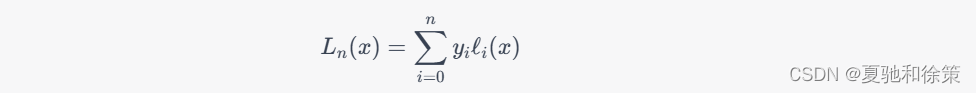
其中，n是已知数据点的个数，y_i是已知数据点在 $x_i$ 处的函数值\\ell_i(x)是拉格朗日基函数，定义为：

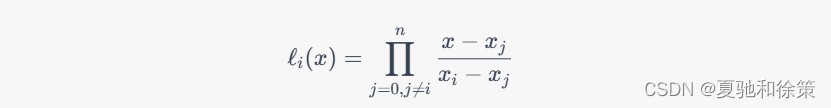
该基函数具有如下性质：

• 在 x = x_i处取值为 1，在 x = x_j（j \\neq i）处取值为 0。
• 该基函数是 n次多项式，且满足 \\ell_i(x_i) = 1，ell_i(x_j) = 0（j \\neq i）。

因此，拉格朗日插值多项式可以通过将每个数据点的函数值 $y_i$ 分别乘以对应的拉格朗日基函数 \\ell_i(x)，并将这些项相加得到。这样构造的多项式函数 $L_n(x)$ 会在每个数据点 (x_i, y_i) 处完全符合原函数的形态，从而实现对原函数的插值。

需要注意的是，拉格朗日插值多项式存在一些问题，如龙格现象和过拟合问题等，因此在实际应用中需要慎重选择插值方法。

 我的理解：

拉格朗日插值多项式是一种插值方法，它通过已知数据点的函数值来构造一个多项式函数，使得该函数能够在这些数据点上完全符合原函数的形态。这种插值方法基于拉格朗日基函数，利用多项式函数的性质来构造插值多项式。

在实际应用中，拉格朗日插值多项式经常用于数据分析、信号处理、数值计算等地方。例如，当我们需要根据已知数据点来估计一个未知函数的值时，可以使用拉格朗日插值多项式来构造一个近似函数，从而实现对未知函数的插值。

需要注意的是，拉格朗日插值多项式的求解需要一定的数学基础，例如多项式函数的定义、导数、微积分、线性代数等等。因此，在学习和应用拉格朗日插值多项式时，需要掌握相关的预备知识。同时，由于拉格朗日插值多项式存在一些问题，如龙格现象和过拟合问题等，因此需要根据实际情况慎重选择插值方法。

 2.2  差商与牛顿基本插值多项式

差商和牛顿基本插值多项式是求解插值多项式的常用方法。下面我来分别介绍一下这两个概念。

差商是插值多项式中的一个重要概念，它用于计算插值多项式的系数。假设我们有 n+1个已知数据点 (x_i,y_i)，其中 i=0,1,\\ldots,n。定义 f[x_i]表示在 x_i处的函数值，即 f[x_i]=y_i，则 k阶差商的定义如下：

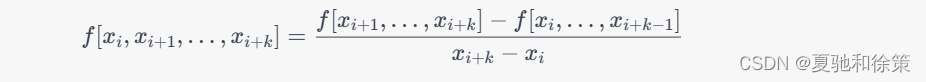
其中，f[x_{i+1},\\ldots,x_{i+k}] 和 f[x_i,\\ldots,x_{i+k-1}] 是 k-1阶差商。根据这个定义，我们可以递归地计算出 k阶差商，从而求出插值多项式的系数。

牛顿基本插值多项式是一种利用差商来求解插值多项式的方法。假设我们有 n+1个已知数据点 (x_i,y_i)，其中 i=0,1,\\ldots,n。定义 f[x_i]表示在 x_i处的函数值，即 f[x_i]=y_i，则牛顿基本插值多项式的形式如下：

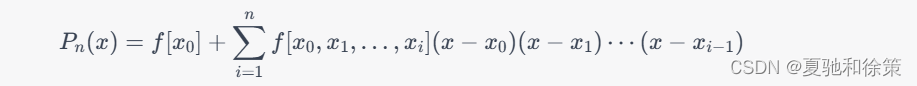
其中，f[x_0,x_1,\\ldots,x_i]表示 i阶差商，可以通过递归地计算差商来求得。牛顿基本插值多项式的优点在于，每增加一个数据点时只需要重新计算最后一个差商，不需要重新计算整个插值多项式，因此计算效率较高。

需要注意的是，牛顿基本插值多项式也存在一些问题，如龙格现象和过拟合问题等。因此，在实际应用中需要慎重选择插值方法，并根据实际情况进行调整。

我的理解：

差商是插值多项式中的一个重要概念，用于计算插值多项式的系数。我们可以将插值多项式看作是通过已知的数据点拟合出来的一个函数，差商则是用来计算这个函数在不同点处的斜率（或者说导数）的值。通过不同阶的差商，我们可以逐步逼近原函数，最终求出插值多项式的系数，从而得到一个近似于原函数的多项式函数。

以牛顿基本插值多项式为例，我们可以将其理解为一个多个线性函数叠加而成的函数，每个线性函数都由一个已知的数据点和对应的斜率（或者说导数）确定。具体来说，每个线性函数都由一个差商和对应的基函数 $x-x_0,x-x_0,x-x_1,x-x_2,...,x-x_{i-1}$ 组成，其中 $x_0,x_1,...,x_{i-1}$ 是已知的数据点，$x$ 是待求的插值点。牛顿基本插值多项式最终得到的就是这些线性函数的叠加，从而得到一个近似于原函数的多项式函数。

需要注意的是，插值多项式的精度受到多个因素的影响，如数据点的数量、数据点的分布、插值点的选择等等。因此，在实际应用中需要根据实际情况进行调整，以获得更好的拟合效果。

2.3 差分与等距结点下的牛顿公式 

差分是数学中的一个概念，用于描述函数值之间的差异。在数值计算中，差分可以用来估计函数的导数、计算积分等等。在插值多项式中，差分的概念也非常重要，可以用来计算插值多项式的系数。

等距结点是指在插值区间内，已知的数据点之间的间距相等。例如，如果在区间 [a,b]内已知 n+1 个数据点 x_0,x_1,...,x_n，并且它们之间的间距相等，即 x_{i+1}-x_i=h，那么这些数据点就是等距结点。在等距结点下，我们可以利用差分的方法，推导出一种用于求解插值多项式的公式，称为牛顿公式。

具体来说，等距结点下的牛顿公式是基于差商的。我们可以定义 f[x_0,x_1]=\\dfrac{f(x_1)-f(x_0)}{x_1-x_0}，称为二阶差商，f[x_0,x_1,x_2]=\\dfrac{f[x_1,x_2]-f[x_0,x_1]}{x_2-x_0}，称为三阶差商，以此类推。利用差商，我们可以推导出一个递推公式：

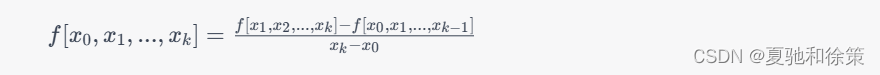
其中 f[x_0,x_1,...,x_k]是 k+1阶差商，f[x_i]=f(x_i) 是已知数据点的函数值。通过这个递推公式，我们可以计算出插值多项式的系数，并得到一个近似于原函数的多项式函数。

需要注意的是，等距结点下的牛顿公式只适用于等距结点的情况，当数据点之间的间距不相等时，需要使用其他的插值方法。此外，牛顿公式的计算复杂度较高，因此在实际应用中需要进行优化，以提高计算效率。

 2.4 多项式插值的内维尔方法

多项式插值的内维尔方法，也称为迭代差商法，是一种用于计算插值多项式系数的方法。它的主要思想是利用差商的递归关系，从而减少计算量。

内维尔方法的基本思想是：将给定的 n+1个节点 x_0, x_1, ..., x_n和相应的函数值 f(x_0), f(x_1), ..., f(x_n)，依次进行差商计算，直到得到插值多项式的系数。具体步骤如下：

1. 将节点和函数值按照自然顺序排列，即 x_0 < x_1 < ... < x_n，f(x_0), f(x_1), ..., f(x_n)。

2. 定义一个 n+1阶差商表格 D，其中第 i行第 j 列的差商 D_{i,j}表示从节点 x_i 到 x_j的 i-j阶差商，即：

   

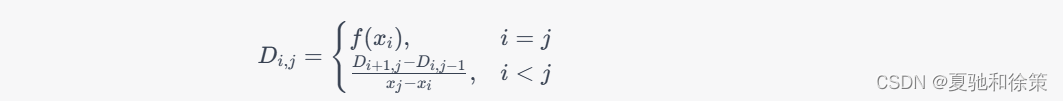
   特别地，D_{i,j}表示从节点 x_i到 x_j的 0阶差商，即 D_{i,i} = f(x_i)。

3. 最后得到的 n次插值多项式为：

    

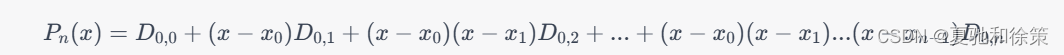
   再一次递归计算，我们可以得到更高次的多项式。

内维尔方法的优点是，它的计算复杂度为 $O(n^2)$，比拉格朗日插值和牛顿插值的复杂度 O(n^3)要低。此外，内维尔方法对于插值点的顺序没有要求，因此它也可以用于非等距插值点的情况。

 我的理解：

多项式插值的内维尔方法是一种用于计算插值多项式系数的递归算法。它的基本思想是利用差商的递归关系，从而减少计算量。

差商是一种计算多项式插值系数的方法。在内维尔方法中，我们定义一个差商表格，其中第 $i$ 行第 j列的差商 D_{i,j}表示从节点 x_i到 x_j的 i-j阶差商。特别地，D_{i,i}表示从节点 x_i到 x_i的 0阶差商，即 D_{i,i} = f(x_i)。

根据差商的定义和递归公式，我们可以通过逐步计算差商表格中的元素来得到插值多项式的系数。具体地，从左上角的 D_{0,0}开始，我们依次计算 D_{0,1}, D_{0,2}, ..., D_{0,n}，其中 n表示节点的数量。然后，我们可以根据递归公式得到 D_{1,1}, D_{1,2}, ..., D_{1,n}，接着计算 D_{2,2}, D_{2,3}, ..., D_{2,n}，以此类推。最后，根据差商的递归关系，我们可以得到插值多项式的系数。

内维尔方法的优点是，它的计算复杂度为 O(n^2)，比拉格朗日插值和牛顿插值的复杂度 O(n^3) 要低。此外，内维尔方法对于插值点的顺序没有要求，因此它也可以用于非等距插值点的情况。

 总结：

下面是对上述方法的重点、难点和易错点的总结：

1. 拉格朗日插值多项式

重点：使用拉格朗日插值多项式求解函数在某个特定点的函数值。

难点：需要求解大量的系数，计算复杂度为 O(n^2)，容易出现数值稳定性问题。

易错点：对于具有大量插值点的问题，使用拉格朗日插值多项式可能导致数值不稳定性和振荡现象。

1. 牛顿插值多项式

重点：使用牛顿插值多项式求解函数在某个特定点的函数值。

难点：需要求解大量的系数，计算复杂度为 O(n^2)，但比拉格朗日插值稳定性更高。

易错点：对于非等距插值点的情况，牛顿插值多项式的计算复杂度可能会变得非常高。

1. 多项式插值的内维尔方法

重点：使用内维尔方法递归计算插值多项式的系数。

难点：需要理解差商的递归公式和差商表格的计算方法。

易错点：如果输入的插值点不是按照升序排列的，则需要进行排序，否则计算出来的插值多项式会有误。此外，如果插值点有重复，则可能会导致除数为零或无法计算差商的情况。