算法设计与智能计算 || 专题六: 不可导凸函数的最优解搜索问题

不可导凸函数的最优解搜索问题
文章目录
1. 次梯度下降方法
如目标函数包含不可微分的部分,形如
E ( w ) = 1 N ∥ y − y ^ ( w ) ∥ 2 2 + λ ⋅ ∥ w ∥ 1 E(\\boldsymbol{w})=\\frac{1}{N}\\Big\\Vert\\boldsymbol{y-\\hat{y}(\\boldsymbol{w})}\\Big\\Vert_2^2+\\lambda\\cdot \\Big\\Vert\\boldsymbol{w}\\Big\\Vert_1 E(w)=N1 y−y^(w) 22+λ⋅ w 1
其最优解则无法使用经典的梯度下降法进行求解。我们需要引入次梯度的概念
次梯度:设 F : R n → R F:\\mathbb{R}^n\\to\\mathbb{R} F:Rn→R 为一个 n n n元函数,如果 g , w ∈ R n \\boldsymbol{g},\\boldsymbol{w}\\in\\mathbb{R}^n g,w∈Rn 满足如下性质:
F ( u ) ≥ F ( w ) + ⟨ g , u − w ⟩ ∀ u ∈ R n F(\\boldsymbol{u})\\ge F(\\boldsymbol{w})+\\lang\\boldsymbol{g},\\boldsymbol{u}-\\boldsymbol{w}\\rang\\;\\;\\; \\forall \\boldsymbol{u}\\in\\mathbb{R}^n F(u)≥F(w)+⟨g,u−w⟩∀u∈Rn
则称 g \\boldsymbol{g} g 是 F F F 在 $ w \\boldsymbol{w} w 处的次梯度。称集合 ∂ F ( u ) = { g ∈ R n : g 为 F 在 w 处的次梯度 } \\partial F(\\boldsymbol{u})=\\{\\boldsymbol{g}\\in\\mathbb{R}^n:\\boldsymbol{g}为F在\\boldsymbol{w}处的次梯度\\} ∂F(u)={g∈Rn:g为F在w处的次梯度} 为 F F F 在 w \\boldsymbol{w} w 处的次梯度.
例:求目标函数 F ( w ) = ∥ w ∥ 1 F(\\boldsymbol{w})=\\Vert \\boldsymbol{w}\\Vert_1 F(w)=∥w∥1 的次梯度。
解:由于 F ( w ) = ∥ w ∥ 1 = ∣ x 1 ∣ + ∣ x 2 ∣ + ⋯ + ∣ x d ∣ F(\\boldsymbol{w})=\\Vert \\boldsymbol{w}\\Vert_1=\\vert x_1\\vert+\\vert x_2\\vert+\\cdots+\\vert x_d\\vert F(w)=∥w∥1=∣x1∣+∣x2∣+⋯+∣xd∣,对任意的分量 F ( w ) = ∣ w ∣ F(w)=\\vert w\\vert F(w)=∣w∣, 则有
F ( u ) ≥ F ( 0 ) + g ⋅ ( u − 0 ) F(u)\\geq F(0) + g\\cdot(u-0) F(u)≥F(0)+g⋅(u−0)
即
∣ u ∣ ≥ ∣ 0 ∣ + g ⋅ ( u − 0 ) \\vert u\\vert\\geq\\vert 0\\vert+g\\cdot(u-0) ∣u∣≥∣0∣+g⋅(u−0)
则
− 1 ≤ g ≤ 1 -1 \\leq g\\leq 1 −1≤g≤1
综上
∂ F ( w ) = { − 1 x < 0 [ − 1 , 1 ] x = 0 1 x > 0 \\partial F(w)=\\left\\{ \\begin{aligned} -1 \\quad x<0\\\\ [-1,1] \\quad x=0\\\\ 1 \\quad x>0\\\\ \\end{aligned} \\right. ∂F(w)=⎩ ⎨ ⎧−1x<0[−1,1]x=01x>0
注意:由于次梯度是一个集合,编程实现时我们只需要取其中一个值即可。
则 ∂ ∥ w ∥ 1 = s i g n ( w ) = { − 1 w < 0 0 w = 0 1 w > 0 \\partial\\Vert \\boldsymbol{w}\\Vert_1 =sign(\\boldsymbol{w})=\\left\\{ \\begin{aligned} \\boldsymbol{-1} \\quad \\boldsymbol{w}<\\boldsymbol{0}\\\\ \\boldsymbol{0} \\quad \\boldsymbol{w}=\\boldsymbol{0}\\\\ \\boldsymbol{1} \\quad \\boldsymbol{w}>\\boldsymbol{0}\\\\ \\end{aligned} \\right. ∂∥w∥1=sign(w)=⎩ ⎨ ⎧−1w<00w=01w>0
1.1 基于次梯度的 Lasso 回归求解
Lasso 回归的目标函数为
F ( w ) = 1 n ∥ X w − y ∥ 2 2 + λ ⋅ ∥ w ∥ 1 F(\\boldsymbol{w})=\\frac{1}{n}\\Big\\Vert\\boldsymbol{Xw-y}\\Big\\Vert_2^2+\\lambda\\cdot \\Big\\Vert\\boldsymbol{w}\\Big\\Vert_1 F(w)=n1 Xw−y 22+λ⋅ w 1
次梯度为
2 n X ⊤ ( X w − y ) + λ ⋅ sign ( w ) ∈ ∂ F ( w ) \\frac{2}{n}\\boldsymbol{X}^\\top\\Big(\\boldsymbol{Xw-y}\\Big)+\\lambda\\cdot \\text{sign}(\\boldsymbol{w})\\in\\partial F(\\boldsymbol{w}) n2X⊤(Xw−y)+λ⋅sign(w)∈∂F(w)
其中
sign ( w ) = { − 1 w < 0 0 w = 0 1 w > 0 \\text{sign}(\\boldsymbol{w})=\\left\\{ \\begin{aligned} \\boldsymbol{-1} \\quad \\boldsymbol{w}<\\boldsymbol{0}\\\\ \\boldsymbol{0} \\quad \\boldsymbol{w}=\\boldsymbol{0}\\\\ \\boldsymbol{1} \\quad \\boldsymbol{w}>\\boldsymbol{0}\\\\ \\end{aligned} \\right. sign(w)=⎩ ⎨ ⎧−1w<00w=01w>0
1.2 次梯度求解 Lasso 算法
| 算法 1: 基于次梯度的lasso回归算法 |
|---|
| 输入: X X X, y \\boldsymbol{y} y |
| 1: \\;\\; w = 0 \\boldsymbol{w}=\\boldsymbol{0} w=0 |
| 2: \\;\\; for t = 1 , 2 , ⋯ , N t=1,2,\\cdots,N t=1,2,⋯,N: |
| 3: e = 2 X T ( X w − y ) / n + s i g n ( w ) \\qquad \\boldsymbol{e}=2X^T(X\\boldsymbol{w}-\\boldsymbol{y})/n+sign(\\boldsymbol{w}) e=2XT(Xw−y)/n+sign(w) ; |
| 4: w = w − α ⋅ e \\qquad \\boldsymbol{w}=\\boldsymbol{w}-\\alpha\\cdot \\boldsymbol{e} w=w−α⋅e ; |
| 5: \\qquad 转入step 3; |
| 输出: w \\boldsymbol{w} w |
1.3 编程实现
# 基于次梯度的lasso回归最优解
# 输入:
# X:m*d维矩阵(其中第一列为全1向量,代表常数项),每一行为一个样本点,维数为d
# y: m维向量
# 参数:
# Lambda: 折中参数
# eta:次梯度下降的步长
# maxIter: 梯度下降法最大迭代步数
# 返回:
# weight:回归方程的系数
class LASSO_SUBGRAD:def __init__(self, Lambda=1,eta=0.1, maxIter=1000):self.Lambda = Lambdaself.eta = etaself.maxIter = maxIterdef fit(self, X, y):n,d = X.shapew = np.zeros((d,1)) self.w = wfor t in range(self.maxIter):e = X@w - yv = 2 * X.T@e / n + self.Lambda * np.sign(w)w = w - self.eta * v self.w += wself.w /= self.maxIterreturn def predict(self, X):return X@self.w
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as pltdef generate_samples(m):X = 2 * (np.random.rand(m, 1) - 0.5) y = X + np.random.normal(0, 0.3, (m,1))return X, ynp.random.seed(100)
X, y = generate_samples(10)
poly = PolynomialFeatures(degree = 10)
X_poly = poly.fit_transform(X)
model = LASSO_SUBGRAD(Lambda=0.001, eta=0.01, maxIter=50000)
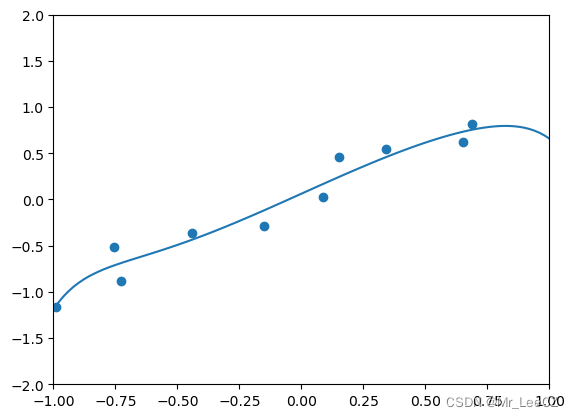
model.fit(X_poly, y)plt.axis([-1, 1, -2, 2])
plt.scatter(X, y)
W = np.linspace(-1, 1, 100).reshape(100, 1)
W_poly = poly.fit_transform(W)
u = model.predict(W_poly)
plt.plot(W, u)
plt.show()
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_scoredef process_features(X):scaler = StandardScaler()X = scaler.fit_transform(X)m, n = X.shapeX = np.c_[np.ones((m, 1)), X] return Xhousing = fetch_california_housing()
X = housing.data
y = housing.target.reshape(-1,1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
X_train = process_features(X_train)
X_test = process_features(X_test)model = LASSO_SUBGRAD(Lambda=0.1)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
score = r2_score(y_test, y_pred)
print("mse = {}, r2 = {}".format(mse, score))
2. 软阈值方法
目标函数
L ( x ) = 1 2 ∥ x − b ∥ 2 2 + γ ∥ x ∥ 1 \\mathcal{L}\\left(\\boldsymbol{x}\\right)=\\frac{1}{2} \\left \\| \\boldsymbol{x}- \\boldsymbol{b}\\right \\|_2^2+\\gamma \\left \\| \\boldsymbol{x} \\right \\|_1 L(x)=21∥x−b∥22+γ∥x∥1
存在问题:不可微分。
策略:转化成分量,即解藕成几个分量的和
L ( x ) = { 1 2 ( x 1 − b 1 ) 2 + γ ∣ x 1 ∣ } + { 1 2 ( x 2 − b 2 ) 2 + γ ∣ x 2 ∣ } + ⋯ + { 1 2 ( x n − b n ) 2 + γ ∣ x n ∣ } \\mathcal{L}\\left(\\boldsymbol{x}\\right)=\\left \\{ \\frac{1}{2} ( x_1- b_1)^2+\\gamma \\left | x_1 \\right | \\right \\}+\\left \\{ \\frac{1}{2} ( x_2- b_2)^2+\\gamma \\left | x_2 \\right | \\right \\}+\\cdots+\\left \\{ \\frac{1}{2} ( x_n- b_n)^2+\\gamma \\left | x_n \\right | \\right \\} L(x)={21(x1−b1)2+γ∣x1∣}+{21(x2−b2)2+γ∣x2∣}+⋯+{21(xn−bn)2+γ∣xn∣}
每个独立的部门均是同一个优化问题
Q ( x ) = 1 2 ( x − b ) 2 + γ ∣ x ∣ x , b ∈ R Q(x)=\\frac{1}{2} ( x- b)^2+\\gamma \\left | x\\right | \\qquad x,b \\in R Q(x)=21(x−b)2+γ∣x∣x,b∈R
对上式关于 x x x求导得:
∂ Q ( x ) ∂ x = x − b + γ ⋅ s i g n ( x ) = 0 \\frac{\\partial Q(x)}{\\partial x}=x-b+\\gamma·sign(x)=0 ∂x∂Q(x)=x−b+γ⋅sign(x)=0
则有
x = b − γ ⋅ s i g n ( x ) ⋯ ( 6 ) x=b-\\gamma·sign(x) \\qquad \\cdots (6) x=b−γ⋅sign(x)⋯(6)
公式(6)中的解 x x x与其符号有很大关系需讨论
(i)当 x > 0 x>0 x>0时, x = b − γ > 0 x=b-\\gamma>0 x=b−γ>0,同时需要 b > γ b>\\gamma b>γ
∙ \\bullet ∙当 b < − γ b<-\\gamma b<−γ时, x = b + Γ x=b+\\Gamma x=b+Γ;
∙ \\bullet ∙当 − γ ≤ b ≤ 0 -\\gamma \\le b \\le 0 −γ≤b≤0时, x x x无极点( x > 0 x>0 x>0), x = 0 x=0 x=0为目标函数最大值。
综上可知
x ^ = S γ ( b ) = { b − γ b > γ 0 − γ ≤ b ≤ γ b + γ b < − γ \\hat{x} =S_\\gamma(b)=\\left\\{\\begin{matrix} b-\\gamma & b>\\gamma\\\\ 0 & -\\gamma\\le b\\le \\gamma\\\\ b+\\gamma & b<-\\gamma \\end{matrix}\\right. x^=Sγ(b)=⎩ ⎨ ⎧b−γ0b+γb>γ−γ≤b≤γb<−γ
或
x ^ = S γ ( b ) = s i g n ( b ) ⋅ m a x { ∣ b ∣ − γ , 0 } \\hat{x} =S_\\gamma(b)=sign(b)·max\\left \\{ \\left | b \\right | -\\gamma,0 \\right \\} x^=Sγ(b)=sign(b)⋅max{∣b∣−γ,0}
3. 坐标下降法求解Lasso回归
坐标下降算法是一种非常常用的机器学习优化搜索算法。坐标下降算法有两个最为重要且优于梯度下降算法的应用场合。第一个场合是梯度不存在或梯度函数较为复杂而难以计算。此时,坐标下降算法是一个比梯度下降算法更为简便且易于实现的算法。Iasso 回归就是一个这样的例子。第二个场合是需要求解带约束的优化间题,梯度下降类算法都是针对无约束的优化问题,而坐标下降算法可以用来求解带约束的优化问题。支持向量机的对得优化问题就是一个这样的例子。
坐标下降算法是一个迭代搜索算法。在搜索过程中的每一步,该算法都选取一个要调整的坐标分量且固定参数的其他各分量的值。然后,沿着选取的分量的坐标轴方向移动到该方向上目标函数值最小的那个点。如此循环使用不同的坐标轴方向,直至沿任何一个坐标轴移动都无法降低目标函数值为止。
给定 w ∈ R n \\boldsymbol{w}\\in\\mathbb{R}^n w∈Rn,对任意 1 ≤ j ≤ n 1\\leq j\\leq n 1≤j≤n,记
w − j = ( w 1 , w 2 , ⋯ , w j − 1 , w j + 1 , ⋯ , w n ) \\boldsymbol{w}_{-j}=(w_1,w_2,\\cdots,w_{j-1},w_{j+1},\\cdots,w_n) w−j=(w1,w2,⋯,wj−1,wj+1,⋯,wn)
则对于 u ∈ R u\\in\\mathbb{R} u∈R,可记做
( u , w − j ) = ( w 1 , w 2 , ⋯ , w j − 1 , u , w j + 1 , ⋯ , w n ) (u,\\boldsymbol{w}_{-j})=(w_1,w_2,\\cdots,w_{j-1},u, w_{j+1},\\cdots,w_n) (u,w−j)=(w1,w2,⋯,wj−1,u,wj+1,⋯,wn)
对单一的坐标
w j ∗ = arg u ∈ R min F ( u , w − j ) w_j^*=\\arg_{u\\in\\mathbb{R}}\\min F(u,\\boldsymbol{w}_{-j}) wj∗=argu∈RminF(u,w−j)
| 算法 2: 坐标下降算法 |
|---|
| 输入: X X X, 每行为 d d d 维向量 |
| 1: \\;\\; w = 0 \\boldsymbol{w}=\\boldsymbol{0} w=0 |
| 2: \\;\\; for t = 1 , 2 , ⋯ , N t=1,2,\\cdots,N t=1,2,⋯,N: |
| 3: j = t % d \\qquad j=t\\%d j=t%d ; |
| 4: w j ∗ = arg u ∈ R min F ( u , w − j ) \\qquad w_j^*=\\arg_{u\\in\\mathbb{R}}\\min F(u,\\boldsymbol{w}_{-j}) wj∗=argu∈RminF(u,w−j) ; |
| 5: w ← ( w j ∗ , w − j ) \\qquad \\boldsymbol{w}\\gets(w_j^*,\\boldsymbol{w}_{-j}) w←(wj∗,w−j) ; |
| 6: \\qquad 转入step 3; |
| 输出: w \\boldsymbol{w} w |
算法 2 虽然给出了求解框架,但是第 4 步的优化问题并非一个简单的问题,特别是目标函数中如果含有不可导的部分。下面以 Lasso 回归为例探索如何求解最优值。
3.1 Lasso 回归的坐标下降法
目标函数
F ( w ) = 1 m ∥ X w − y ∥ 2 2 + λ ⋅ ∥ w ∥ 1 F(\\boldsymbol{w})=\\frac{1}{m}\\Big\\Vert\\boldsymbol{Xw-y}\\Big\\Vert_2^2+\\lambda\\cdot \\Big\\Vert\\boldsymbol{w}\\Big\\Vert_1 F(w)=m1 Xw−y 22+λ⋅ w 1
或
F ( w ) = 1 m ∑ i = 1 m ( ⟨ w , x ( i ) ⟩ − y i ) 2 + λ ⋅ ∥ w ∥ 1 F(\\boldsymbol{w})=\\frac{1}{m}\\sum_{i=1}^m\\Big(\\lang\\boldsymbol{w},\\boldsymbol{x}^{(i)}\\rang-y_i\\Big)^2+\\lambda\\cdot \\Big\\Vert\\boldsymbol{w}\\Big\\Vert_1 F(w)=m1i=1∑m(⟨w,x(i)⟩−yi)2+λ⋅ w 1
对于分量 u u u,目标函数可表示为
F ( u ) = 1 m ∑ i = 1 m ( ⟨ w , x ( i ) ⟩ − y i ) 2 + λ ⋅ ∥ w ∥ 1 = 1 m ∑ i = 1 m ( u ⋅ x j ( i ) + ⟨ w − j , x − j ( i ) ⟩ − y i ⏟ e j ( i ) ) 2 + λ ⋅ ∣ u ∣ + λ ⋅ ∥ w − j ∥ 1 = 1 m ∑ i = 1 m ( u ⋅ x j ( i ) + e j ( i ) ) 2 + λ ⋅ ∣ u ∣ + λ ⋅ ∥ w − j ∥ 1 \\begin{align*} F(u)&=\\frac{1}{m}\\sum_{i=1}^m\\Big(\\lang\\boldsymbol{w},\\boldsymbol{x}^{(i)}\\rang-y_i\\Big)^2+\\lambda\\cdot \\Big\\Vert\\boldsymbol{w}\\Big\\Vert_1\\\\ &=\\frac{1}{m}\\sum_{i=1}^m\\Big(u\\cdot x_j^{(i)}+\\underbrace{\\lang\\boldsymbol{w}_{-j},\\boldsymbol{x}_{-j}^{(i)}\\rang-y_i}_{e_j^{(i)}}\\Big)^2+\\lambda\\cdot\\vert u\\vert+\\lambda\\cdot \\Big\\Vert\\boldsymbol{w}_{-j}\\Big\\Vert_1\\\\ &=\\frac{1}{m}\\sum_{i=1}^m\\Big(u\\cdot x_j^{(i)}+e_j^{(i)}\\Big)^2+\\lambda\\cdot\\vert u\\vert+\\lambda\\cdot \\Big\\Vert\\boldsymbol{w}_{-j}\\Big\\Vert_1\\\\ \\end{align*} F(u)=m1i=1∑m(⟨w,x(i)⟩−yi)2+λ⋅ w 1=m1i=1∑m(u⋅xj(i)+ej(i) ⟨w−j,x−j(i)⟩−yi)2+λ⋅∣u∣+λ⋅ w−j 1=m1i=1∑m(u⋅xj(i)+ej(i))2+λ⋅∣u∣+λ⋅ w−j 1
目标函数的次梯度为
2 m ∑ i = 1 m ( u ⋅ x j ( i ) + e j ( i ) ) ⋅ x j ( i ) + λ ⋅ ∣ u ∣ = { 2 m ∑ i = 1 m ( x j ( i ) ) 2 } ⏟ α j ⋅ u + { 2 m ∑ i = 1 m ( x j ( i ) e j ( i ) ) } ⏟ β j + λ ⋅ ∣ u ∣ = α j ⋅ u + β j + λ ⋅ ∣ u ∣ ∈ ∂ F ( u ) = { α j ⋅ u + β j + λ u > 0 [ α j ⋅ u + β j − λ , α j ⋅ u + β j + λ ] u = 0 α j ⋅ u + β j − λ u < 0 \\begin{align*} &\\frac{2}{m}\\sum_{i=1}^m\\Big(u\\cdot x_j^{(i)}+e_j^{(i)}\\Big)\\cdot x_j^{(i)}+\\lambda\\cdot\\vert u\\vert\\\\ =&\\underbrace{\\Bigg\\{\\frac{2}{m}\\sum_{i=1}^m \\Big(x_j^{(i)}\\Big)^2\\Bigg\\}}_{\\alpha_j}\\cdot u +\\underbrace{\\Bigg\\{\\frac{2}{m}\\sum_{i=1}^m \\Big(x_j^{(i)}e_j^{(i)}\\Big)\\Bigg\\}}_{\\beta_j}+\\lambda\\cdot\\vert u\\vert\\\\ =&\\alpha_j\\cdot u+\\beta_j+\\lambda\\cdot\\vert u\\vert\\in\\partial F(u)\\\\ =&\\left\\{\\begin{matrix} \\alpha_j\\cdot u+\\beta_j+\\lambda & u>0\\\\ [ \\alpha_j\\cdot u+\\beta_j-\\lambda,\\alpha_j\\cdot u+\\beta_j+\\lambda] & u=0\\\\ \\alpha_j\\cdot u+\\beta_j-\\lambda & u<0 \\end{matrix}\\right. \\end{align*} ===m2i=1∑m(u⋅xj(i)+ej(i))⋅xj(i)+λ⋅∣u∣αj {m2i=1∑m(xj(i))2}⋅u+βj {m2i=1∑m(xj(i)ej(i))}+λ⋅∣u∣αj⋅u+βj+λ⋅∣u∣∈∂F(u)⎩ ⎨ ⎧αj⋅u+βj+λ[αj⋅u+βj−λ,αj⋅u+βj+λ]αj⋅u+βj−λu>0u=0u<0
由于 α j > 0 \\alpha_j>0 αj>0 且 0 ∈ ∂ F ( u ) 0\\in \\partial F(u) 0∈∂F(u),则有
当 u > 0 u>0 u>0 时,我们需要 α j ⋅ u ⏟ > 0 + β j + λ = 0 \\underbrace{\\alpha_j\\cdot u}_{>0}+\\beta_j+\\lambda=0 >0 αj⋅u+βj+λ=0,即 β j + λ < 0 \\beta_j+\\lambda<0 βj+λ<0 或 β j < − λ \\beta_j<-\\lambda βj<−λ,此时的 u u u 满足:
{ α j ⋅ u + β j + λ = 0 u > 0 \\left\\{\\begin{matrix} \\alpha_j\\cdot u+\\beta_j+\\lambda=0\\\\ u>0 \\end{matrix}\\right. {αj⋅u+βj+λ=0u>0
即
u = − β j α j − λ α j u=-\\frac{\\beta_j}{ \\alpha_j}-\\frac{\\lambda}{ \\alpha_j} u=−αjβj−αjλ
当 u < 0 u<0 u<0 时,我们需要 α j ⋅ u ⏟ < 0 + β j − λ = 0 \\underbrace{\\alpha_j\\cdot u}_{<0}+\\beta_j-\\lambda=0 <0 αj⋅u+βj−λ=0,即 β j − λ > 0 \\beta_j-\\lambda>0 βj−λ>0 或 β j > λ \\beta_j>\\lambda βj>λ,此时的 u u u 满足:
{ α j ⋅ u + β j − λ = 0 u < 0 \\left\\{\\begin{matrix} \\alpha_j\\cdot u+\\beta_j-\\lambda=0\\\\ u<0 \\end{matrix}\\right. {αj⋅u+βj−λ=0u<0
即
u = − β j α j + λ α j u=-\\frac{\\beta_j}{ \\alpha_j}+\\frac{\\lambda}{ \\alpha_j} u=−αjβj+αjλ
当 u = 0 u=0 u=0 时,满足 0 ∈ [ α j ⋅ u + β j − λ , α j ⋅ u + β j + λ ] 0\\in[ \\alpha_j\\cdot u+\\beta_j-\\lambda,\\alpha_j\\cdot u+\\beta_j+\\lambda] 0∈[αj⋅u+βj−λ,αj⋅u+βj+λ],即 β j − λ < 0 \\beta_j-\\lambda<0 βj−λ<0 且 β j + λ > 0 \\beta_j+\\lambda>0 βj+λ>0,即 − λ < β j < λ -\\lambda<\\beta_j<\\lambda −λ<βj<λ
综上
u ∗ = { − β j α j + λ α j β j > λ 0 − λ < β j < λ − β j α j − λ α j β j < − λ = { − β j α j + λ α j β j α j > λ α j 0 − λ α j < β j α j < λ α j − β j α j − λ α j β j α j < − λ α j = { − β j α j + λ α j − β j α j < − λ α j 0 − λ α j < − β j α j < λ α j − β j α j − λ α j − β j α j > λ α j = S λ α j ( − β j α j ) \\begin{align*} u^*=&\\left\\{\\begin{matrix} -\\frac{\\beta_j}{ \\alpha_j}+\\frac{\\lambda}{ \\alpha_j} & \\beta_j>\\lambda\\\\\\\\ 0 & -\\lambda<\\beta_j<\\lambda\\\\\\\\ -\\frac{\\beta_j}{ \\alpha_j}-\\frac{\\lambda}{ \\alpha_j} & \\beta_j<-\\lambda \\end{matrix}\\right.\\\\\\\\ =&\\left\\{\\begin{matrix} -\\frac{\\beta_j}{ \\alpha_j}+\\frac{\\lambda}{ \\alpha_j} & \\frac{\\beta_j}{ \\alpha_j}>\\frac{\\lambda}{ \\alpha_j} \\\\\\\\ 0 & -\\frac{\\lambda}{ \\alpha_j} <\\frac{\\beta_j}{ \\alpha_j}<\\frac{\\lambda}{ \\alpha_j} \\\\\\\\ -\\frac{\\beta_j}{ \\alpha_j}-\\frac{\\lambda}{ \\alpha_j} & \\frac{\\beta_j}{ \\alpha_j}<-\\frac{\\lambda}{ \\alpha_j} \\end{matrix}\\right.\\\\\\\\ =&\\left\\{\\begin{matrix} -\\frac{\\beta_j}{ \\alpha_j}+\\frac{\\lambda}{ \\alpha_j} & -\\frac{\\beta_j}{ \\alpha_j}<-\\frac{\\lambda}{ \\alpha_j} \\\\\\\\ 0 & -\\frac{\\lambda}{ \\alpha_j} <-\\frac{\\beta_j}{ \\alpha_j}<\\frac{\\lambda}{ \\alpha_j} \\\\\\\\ -\\frac{\\beta_j}{ \\alpha_j}-\\frac{\\lambda}{ \\alpha_j} & -\\frac{\\beta_j}{ \\alpha_j}>\\frac{\\lambda}{ \\alpha_j} \\end{matrix}\\right.\\\\\\\\ =&S_{\\frac{\\lambda}{ \\alpha_j} }( -\\frac{\\beta_j}{ \\alpha_j}) \\end{align*} u∗====⎩ ⎨ ⎧−αjβj+αjλ0−αjβj−αjλβj>λ−λ<βj<λβj<−λ⎩ ⎨ ⎧−αjβj+αjλ0−αjβj−αjλαjβj>αjλ−αjλ<αjβj<αjλαjβj<−αjλ⎩ ⎨ ⎧−αjβj+αjλ0−αjβj−αjλ−αjβj<−αjλ−αjλ<−αjβj<αjλ−αjβj>αjλSαjλ(−αjβj)
3.2 Lasso 回归的坐标下降算法
算法:
| 算法 3: Lasso 回归的坐标下降算法 |
|---|
| 输入: X X X, 每行为 d d d 维向量 |
| 1: \\;\\; w = 0 \\boldsymbol{w}=\\boldsymbol{0} w=0 |
| 2: \\;\\; α = [ 2 m ∑ i = 1 m ( x j ( i ) ) 2 ] \\alpha=\\Bigg[\\frac{2}{m}\\sum_{i=1}^m \\Big(x_j^{(i)}\\Big)^2\\Bigg] α=[m2∑i=1m(xj(i))2] |
| 3: \\;\\; for t = 1 , 2 , ⋯ , N t=1,2,\\cdots,N t=1,2,⋯,N: |
| 4: j = t % d \\qquad j=t\\%d j=t%d ; |
| 5: w j = 0 \\qquad w_j=0 wj=0 ; |
| 6: e j = X w − y \\qquad e_j=Xw-y ej=Xw−y ; |
| 7: β j = 2 m ∑ i = 1 m ( x j ( i ) e j ( i ) ) \\qquad \\beta_j=\\frac{2}{m}\\sum_{i=1}^m \\Big(x_j^{(i)}e_j^{(i)}\\Big) βj=m2∑i=1m(xj(i)ej(i)) ; |
| 8: w j = S h i n k ( − β j α j , λ α j ) \\qquad w_j=Shink(-\\frac{\\beta_j}{ \\alpha_j},\\frac{\\lambda}{ \\alpha_j}) wj=Shink(−αjβj,αjλ) ; |
| 9: \\qquad 转入step 4; |
| 输出: w \\boldsymbol{w} w |
3.3 Lasso 回归的坐标下降算法实现
# 基于坐标下降法的lasso回归最优解
# 输入:
# X:m*d维矩阵(其中第一列为全1向量,代表常数项),每一行为一个样本点,维数为d
# y: m维向量
# 参数:
# Lambda: 折中参数
# maxIter: 梯度下降法最大迭代步数
# 返回:
# weight:回归方程的系数
class LASSO_ADMM: def __init__(self, Lambda=1, maxIter=1000):self.lambda_ = Lambdaself.maxIter = maxIterdef soft_threshold(self, t, x):if x>t:return x-telif x>=-t:return 0else:return x+tdef fit(self, X, y):m,n = X.shapealpha = 2 * np.sum(X2, axis=0) / mw = np.zeros(n)for t in range(self.maxIter):j = t % nw[j]=0e_j = X@(w.reshape(-1,1)) - ybeta_j = 2 * X[:, j]@e_j / mu = self.soft_threshold(self.lambda_/alpha[j], -beta_j/alpha[j])w[j] = uself.w = wdef predict(self, X):return X@(self.w.reshape(-1,1))
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_scoredef process_features(X):scaler = StandardScaler()X = scaler.fit_transform(X)m, n = X.shapeX = np.c_[np.ones((m, 1)), X] return Xhousing = fetch_california_housing()
X = housing.data
y = housing.target.reshape(-1,1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
X_train = process_features(X_train)
X_test = process_features(X_test)model = LASSO_ADMM(Lambda=0.1, maxIter=1000)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
score = r2_score(y_test, y_pred)
print("mse = {}, r2 = {}".format(mse, score))
4. 基于ADMM 方法的 Lasso 回归
目标函数
x ∗ = a r g m i n x 1 2 ∥ A x − b ∥ 2 2 + α ∥ x ∥ 1 \\boldsymbol{x}^*=argmin_{\\boldsymbol{x}}\\frac{1}{2}\\left \\| A\\boldsymbol{x}-\\boldsymbol{b} \\right \\|_2^2+\\alpha \\left \\| \\boldsymbol{x} \\right \\|_1 x∗=argminx21∥Ax−b∥22+α∥x∥1
可变形为复合优化
m i n x , z 1 2 ∥ A x − b ∥ 2 2 + α ∥ z ∥ 1 s . t x = z min_{\\boldsymbol{x},\\boldsymbol z}\\frac{1}{2}\\left \\| A\\boldsymbol{x}-\\boldsymbol{b} \\right \\|_2^2+\\alpha \\left \\| \\boldsymbol z \\right \\|_1\\\\ s.t \\qquad \\boldsymbol{x}=\\boldsymbol z minx,z21∥Ax−b∥22+α∥z∥1s.tx=z
构造增广拉格朗日函数为:
L ( x , z , u ) = 1 2 ∥ A x − b ∥ 2 2 + α ∥ z ∥ 1 + ⟨ u , x − z ⟩ + β 2 ∥ x − z ∥ 2 2 \\mathcal{L}\\left( \\boldsymbol{x},\\boldsymbol z,\\boldsymbol{u}\\right)=\\frac{1}{2}\\left \\| A\\boldsymbol{x}-\\boldsymbol{b} \\right \\|_2^2+\\alpha \\left \\| \\boldsymbol z \\right \\|_1+\\left \\langle \\boldsymbol{u}, \\boldsymbol{x}-\\boldsymbol z\\right \\rangle+\\frac{\\beta}{2} \\left \\| \\boldsymbol{x}-\\boldsymbol z \\right \\| _2^2 L(x,z,u)=21∥Ax−b∥22+α∥z∥1+⟨u,x−z⟩+2β∥x−z∥22
∙ \\bullet ∙迭代步骤:
step 1
( x ∗ , z ∗ ) = a r g m i n x , ς L ( w , z , u ∗ ) (\\boldsymbol{x}^*,\\boldsymbol z^*)=argmin_{\\boldsymbol{x},\\boldsymbol\\varsigma}\\mathcal{L}\\left( \\boldsymbol{w},\\boldsymbol z,\\boldsymbol{u^*}\\right) (x∗,z∗)=argminx,ςL(w,z,u∗)
step 2
u = u + β ( x − z ) \\boldsymbol{u}=\\boldsymbol{u}+\\beta(\\boldsymbol{x}-\\boldsymbol z) u=u+β(x−z)
∙ \\bullet ∙将步骤<1>拆解成两个子问题<1.1>和<1.2>
tesp 1.1
x ∗ = arg min x L ( x , z ∗ , u ∗ ) = arg min x 1 2 ∥ A x − b ∥ 2 2 + ⟨ u , x − z ⟩ + β 2 ∥ x − z ∥ 2 2 = arg min x 1 2 ∥ A x − b ∥ 2 2 + u ⊤ ( x − z ) + β 2 ∥ x − z ∥ 2 2 \\begin{array}{ll} \\boldsymbol{x}^*&=\\argmin_{\\boldsymbol{x}}\\mathcal{L}\\left( \\boldsymbol{x},\\boldsymbol z^*,\\boldsymbol{u^*}\\right)\\\\ &=\\argmin_{\\boldsymbol{x}}\\frac{1}{2}\\left \\| A\\boldsymbol{x}-\\boldsymbol{b} \\right \\|_2^2+\\left \\langle \\boldsymbol{u}, \\boldsymbol{x}-\\boldsymbol z\\right \\rangle+\\frac{\\beta}{2} \\left \\| \\boldsymbol{x}-\\boldsymbol z \\right \\| _2^2\\\\ &=\\argmin_{\\boldsymbol{x}}\\frac{1}{2}\\left \\| A\\boldsymbol{x}-\\boldsymbol{b} \\right \\|_2^2+\\boldsymbol{u}^{\\top}(\\boldsymbol{x}-\\boldsymbol z)+\\frac{\\beta}{2} \\left \\| \\boldsymbol{x}-\\boldsymbol z \\right \\| _2^2 \\end{array} x∗=argminxL(x,z∗,u∗)=argminx21∥Ax−b∥22+⟨u,x−z⟩+2β∥x−z∥22=argminx21∥Ax−b∥22+u⊤(x−z)+2β∥x−z∥22
记 Q ( x ) = 1 2 ∥ A x − b ∥ 2 2 + u ⊤ ( x − z ) + β 2 ∥ x − z ∥ 2 2 Q(\\boldsymbol{x})=\\frac{1}{2}\\left \\| A\\boldsymbol{x}-\\boldsymbol{b} \\right \\|_2^2+\\boldsymbol{u}^{\\top}(\\boldsymbol{x}-\\boldsymbol z)+\\frac{\\beta}{2} \\left \\| \\boldsymbol{x}-\\boldsymbol z \\right \\| _2^2 Q(x)=21∥Ax−b∥22+u⊤(x−z)+2β∥x−z∥22
∂ Q ( x ) ∂ x = A ⊤ ( A x − b ) + u + β ( x − z ) = ( A ⊤ A + β I ) x − ( A ⊤ b + β z − u ) = 0 \\begin{array}{ll} \\frac{\\partial Q(\\boldsymbol{x})}{\\partial \\boldsymbol{x}}&=A^{\\top}(A\\boldsymbol{x}-\\boldsymbol{b})+\\boldsymbol{u}+\\beta(\\boldsymbol{x}-\\boldsymbol z)\\\\ &=(A^{\\top}A+\\beta I)\\boldsymbol{x}-(A^{\\top}\\boldsymbol{b}+\\beta\\boldsymbol z-\\boldsymbol{u})=0 \\end{array} ∂x∂Q(x)=A⊤(Ax−b)+u+β(x−z)=(A⊤A+βI)x−(A⊤b+βz−u)=0
即
x ∗ = ( A ⊤ A + β I ) − 1 ( A ⊤ b + β z − u ) \\boldsymbol{x}^*=(A^{\\top}A+\\beta I)^{-1}(A^{\\top}\\boldsymbol{b}+\\beta\\boldsymbol z-\\boldsymbol{u}) x∗=(A⊤A+βI)−1(A⊤b+βz−u)
step 1.2
z ∗ = a r g m i n z L ( x ∗ , z , u ∗ ) = arg min z β 2 ∥ x − z + 1 β u ∥ 2 2 + α ∥ z ∥ 1 = arg min z β 2 ∥ x + 1 β u ‾ − z ∥ 2 2 + α β ‾ ∥ z ∥ 1 \\begin{array}{ll} \\boldsymbol{z}^*&=argmin_{\\boldsymbol{z}}\\mathcal{L}\\left( \\boldsymbol{x}^*,\\boldsymbol z,\\boldsymbol{u^*}\\right)\\\\ &=\\argmin_{\\boldsymbol{z}}\\frac{\\beta}{2}\\left \\| \\boldsymbol{x}-\\boldsymbol z+\\frac{1}{\\beta}\\boldsymbol{u} \\right \\| _2^2+\\alpha\\left \\| \\boldsymbol z \\right \\|_1\\\\ &=\\argmin_{\\boldsymbol{z}}\\frac{\\beta}{2}\\left \\|\\underline{ \\boldsymbol{x}+\\frac{1}{\\beta}\\boldsymbol{u}} -\\boldsymbol z\\right \\| _2^2+\\underline{\\frac{\\alpha}{\\beta}}\\left \\| \\boldsymbol z \\right \\|_1 \\end{array} z∗=argminzL(x∗,z,u∗)=argminz2β x−z+β1u 22+α∥z∥1=argminz2β x+β1u−z 22+βα∥z∥1
则
z ∗ = S α β ( x + 1 β u ) \\boldsymbol{z}^*=S_{\\frac{\\alpha}{\\beta}}(\\boldsymbol{x}+\\frac{1}{\\beta}\\boldsymbol{u}) z∗=Sβα(x+β1u)
4.1 Lasso 回归的 ADMM 算法
| 算法: Lasso 回归的 ADMM 算法 |
|---|
| 输入: 数据数据矩阵 A A A |
| 1: \\;\\; 初始化: z ( 0 ) = 0 , u ( 0 ) = 0 \\boldsymbol z^{(0)}=0,\\boldsymbol{u}^{(0)}=0 z(0)=0,u(0)=0 |
| 2: \\;\\; While not converged do |
| 3: \\qquad 计算权重系数 x \\boldsymbol{x} x: x ( k + 1 ) = ( A ⊤ A + β I ) − 1 ( A ⊤ b + β z ( k ) − u ( k ) ) \\boldsymbol{x}^{(k+1)}=(A^{\\top}A+\\beta I)^{-1}(A^{\\top}\\boldsymbol{b}+\\beta\\boldsymbol z^{(k)}-\\boldsymbol{u}^{(k)}) x(k+1)=(A⊤A+βI)−1(A⊤b+βz(k)−u(k)) |
| 4: \\qquad 计算 z \\boldsymbol{z} z: z ( k + 1 ) = S α β ( x ( k + 1 ) + 1 β u ( k ) ) \\boldsymbol z^{(k+1)}=S_{\\frac{\\alpha}{\\beta}}(\\boldsymbol{x}^{(k+1)}+\\frac{1}{\\beta}\\boldsymbol{u}^{(k)}) z(k+1)=Sβα(x(k+1)+β1u(k)) |
| 5: \\qquad 计算 u \\boldsymbol{u} u: u ( k + 1 ) = u ( k ) + β ( x ( k + 1 ) − z ( k + 1 ) ) \\boldsymbol{u}^{(k+1)}=\\boldsymbol{u}^{(k)}+\\beta(\\boldsymbol{x}^{(k+1)}-\\boldsymbol z^{(k+1)}) u(k+1)=u(k)+β(x(k+1)−z(k+1)) |
| 6: \\;\\; end While |
| 输出: 稀疏解 u \\boldsymbol{u} u |


