算法设计与智能计算 || 专题七: 主成分分析的统计学视角

文章列表

主成分分析的统计学视角

文章目录

主成分分析的统计学视角
PCA 的统计学视角
- 1. 寻找第一个主成分
- 2. 获取第二个主成分
- 3. 非零均值随机变量的主元
- 4. 零均值随机变量的样本主元
- 5. PCA 降维案例

主成分分析是将高维空间中的数据集拟合成一个低维子空间的方法，到目前为止它已成功应用于数学建模、数据压缩、数据可视化等地方。

主成分分析是将高维空间的数据集 $\\{\\boldsymbol{x}_i\\in\\mathbb{R}^D\\vert i=1,2,\\cdots,n\\}$ 拟合到一个低维放射子空间 $S$ 中，且其维数 $d\\ll D$ 。该问题可视为统计问题或者代数几何问题。

PCA 的统计学视角

多维随机变量 $\\boldsymbol{x}\\in \\mathbb{R}^D$ 满足 $\\mathbb{E}[\\boldsymbol{x}]=\\boldsymbol{0}$ ，可寻找 $d\\;\\;(\\ll D)$ 个主元 $y_i\\;\\;(i=1,2,\\cdots,d)$ ，使 $\\boldsymbol{y}=[y_1,y_2,\\cdots,y_d]^\\top$ 可表示为 $\\boldsymbol{x}$ 的 $d$ 个不线性相关的成分
$\\boldsymbol{y}=\\begin{bmatrix} y_1\\\\ y_2 \\\\ \\vdots \\\\ y_d \\end{bmatrix} =\\begin{bmatrix} \\boldsymbol{u}_1^\\top\\boldsymbol{x}\\\\ \\boldsymbol{u}_2^\\top\\boldsymbol{x}\\\\ \\vdots \\\\ \\boldsymbol{u}_d^\\top\\boldsymbol{x}\\\\ \\end{bmatrix} =\\begin{bmatrix} \\boldsymbol{u}_1^\\top\\\\ \\boldsymbol{u}_2^\\top\\\\ \\vdots \\\\ \\boldsymbol{u}_d^\\top\\\\ \\end{bmatrix}\\boldsymbol{x} =U^\\top\\boldsymbol{x}$
或
$y_i=\\boldsymbol{u}_i^\\top\\boldsymbol{x},\\qquad i=1,2,\\cdots,d$
满足 $\\boldsymbol{u}_i^\\top\\boldsymbol{u}_i=1,\\;\\;\\boldsymbol{u}_i^\\top\\boldsymbol{u}_j=0$ 且 $\\text{Var}[y_1]\\geq \\text{Var}[y_2]\\geq\\cdots\\geq\\text{Var}[y_d]$ ，其中， $y_1,y_2,\\cdots,y_d$ 分别称为 $\\boldsymbol{x}$ 的第1、第2、 $\\cdots$ 、第 $d$ 个主成分.

1. 寻找第一个主成分

以第一主成分为例，我们试图寻找向量 $\\boldsymbol{u}_1^*$ 使得
$\\begin{align*} \\max_{\\boldsymbol{u}_1^*\\in\\mathbb{R}^D} \\quad \\text{Var}[\\boldsymbol{u}_1^{\\top}\\boldsymbol{x}] \\\\ s.t. \\quad\\boldsymbol{u}_1^{\\top}\\boldsymbol{u}_1=1 \\end{align*}$
定理：（随机变量的主成分）

对于随机变量 $\\boldsymbol{x}\\in\\mathbb{R}^D$ 且满足 $\\mathbb{E}[\\boldsymbol{x}]=\\boldsymbol{0}$ ，协方差矩阵为 $\\Sigma_{\\boldsymbol{x}}=\\mathbb{E}[\\boldsymbol{x}\\boldsymbol{x}^\\top]$ ，假设 $\\text{rank}(\\Sigma_{\\boldsymbol{x}})\\geq d$ ，则多维随机变量 $\\boldsymbol{x}$ 的第 $i$ 个主成分 $y_i$ 可表示为
$y_i=\\boldsymbol{u}_i^\\top\\boldsymbol{x}$
其中， $\\{\\boldsymbol{u}_i\\}_{i=1}^d$ 是协方差矩阵 $\\Sigma_{\\boldsymbol{x}}$ 的第 $i$ 个最大特征值对应的特征向量（相互正交），且 $\\boldsymbol\\lambda_i=\\text{Var}[\\boldsymbol y_i]$ .

证明： 为简单起见，假定 $\\Sigma_{\\boldsymbol{x}}$ 无重复特征值。由 $\\Sigma_{\\boldsymbol{x}}\\boldsymbol{u}_j=\\lambda_j\\boldsymbol{u}_j$ 或 $\\boldsymbol{u}_j^\\top\\Sigma_{\\boldsymbol{x}}=\\lambda_j\\boldsymbol{u}_j^\\top$ 知
$\\boldsymbol{u}_i^\\top\\underbrace{\\Sigma_{\\boldsymbol{x}}\\boldsymbol{u}_j}=\\lambda_j\\boldsymbol{u}_i^\\top\\boldsymbol{u}_j\\\\ \\underbrace{\\boldsymbol{u}_i^\\top\\Sigma_{\\boldsymbol{x}}}\\boldsymbol{u}_j=\\lambda_i\\boldsymbol{u}_i^\\top\\boldsymbol{u}_j$
即 $(\\boldsymbol\\lambda_i-\\boldsymbol\\lambda_j)\\boldsymbol{u}_i^\\top\\boldsymbol{u}_j=0$ ，又由于 $\\boldsymbol\\lambda_i\\ne\\boldsymbol\\lambda_j$ ，可知 $\\boldsymbol{u}_i^\\top\\boldsymbol{u}_j=0$

由于
$\\begin{aligned} \\operatorname{Var}\\left[\\boldsymbol y_{i}\\right] &=\\operatorname{Var}\\left[\\boldsymbol{u_{i}^{\\top}} \\boldsymbol x\\right]=E\\left[\\left(u_{i}^{\\top} x\\right)^{2}\\right] \\\\ &=E\\left[\\boldsymbol {u_{i}^{\\top}} \\boldsymbol x \\boldsymbol{x^{\\top}} \\boldsymbol u_{i}\\right]=\\boldsymbol{u_{i}^{\\top}} E\\left[\\boldsymbol x \\boldsymbol{x^{\\top}}\\right] u_{i}=\\boldsymbol u_{i} \\Sigma_{x} \\boldsymbol u_{i} \\end{aligned}$
则优化问题 $\\max \\operatorname{Var}\\left[\\boldsymbol y_{1}\\right]$ 可建模为
$\\left\\{\\begin{array}{l} \\max _{\\boldsymbol{u}_1\\in\\mathbb{R}^D} \\boldsymbol u_1^{\\top} \\Sigma_x \\boldsymbol u_1 \\\\ \\text { s.t. } \\boldsymbol{u_1^{\\top}} \\boldsymbol u_1=1 \\end{array}\\right.$

构造拉格朗日函数，将约束优化化成无约束优化
$\\mathcal{L}\\left( \\boldsymbol{u}_{1}\\right)= \\boldsymbol{u}_{1}^{\\top} \\ {\\Sigma}_{\\boldsymbol{x}} \\boldsymbol{u}_{1}+\\boldsymbol{\\lambda}\\left(1-\\boldsymbol{{u}_{1}^{\\top}} \\boldsymbol{u}_{1}\\right)$
偏导数值为零
$\\frac{\\partial \\mathcal{L}\\left(\\boldsymbol{u}_{1}\\right)}{\\partial \\boldsymbol{u}_{1}}=2 \\ {\\Sigma}_{x} \\boldsymbol{u}_{1}-2 \\boldsymbol{\\lambda} \\boldsymbol {u}_{1}=2\\left(\\ {\\Sigma}_{x} \\boldsymbol {u}_{1}-\\boldsymbol\\lambda \\boldsymbol {u}_{1}\\right)=0$
即
${\\Sigma}_{x} \\boldsymbol {u}_{1}=\\boldsymbol \\lambda \\boldsymbol {u}_{1}$
可知 ${u}_{1}$ 是协方差矩阵 ${\\sum}_{x}$ 的特征值 $\\boldsymbol\\lambda$ 对应的特征向量，最优值 $\\boldsymbol{ {u}_{1}^{\\top}} {\\sum}_{x} \\boldsymbol u_{1}=\\boldsymbol\\lambda \\boldsymbol u_{1} \\boldsymbol{u_{1}^{\\top}}=\\boldsymbol\\lambda_{1}>0$ 。

2. 获取第二个主成分

第二个最优解 $\\boldsymbol{u}_2$ 需要满足随机变量 $y_{1}=\\boldsymbol{u_{1}^{\\top}} \\boldsymbol x$ 与随机变量 $y_{2}=\\boldsymbol{u_{2}^{\\top}} \\boldsymbol x$ 不相关，即 $\\boldsymbol {u}_{1} \\perp \\boldsymbol {u}_{2}$ . 由于 $\\mathbb{E}[\\boldsymbol x]=\\boldsymbol 0$ ，则 $\\mathbb{E}[y_i]=\\mathbb{E}[\\boldsymbol u^\\top_i\\boldsymbol x]=0$ . 两个随机变量的协方差可表示为
$\\begin{array}{l} \\operatorname{Cov}\\left(y_{1}, y_{2}\\right)=\\operatorname{Cov}\\left(\\boldsymbol {{u}_{1}^{\\top}} \\boldsymbol x, \\boldsymbol {u_{2}^{\\top}}\\boldsymbol x\\right)=E\\left[\\left(\\boldsymbol{u_{1}^{\\top}} \\boldsymbol x\\right)\\left(\\boldsymbol{u_{2}^{\\top}} \\boldsymbol x\\right)^{\\top}\\right] \\\\ =E\\left[\\boldsymbol {{u}_{1}^{\\top}} \\boldsymbol x \\boldsymbol{x^{\\top}} \\boldsymbol {u}_{2}\\right]=\\boldsymbol {{u}_{1}^{\\top}} \\Sigma_{\\boldsymbol x} \\boldsymbol {u}_{2}=\\boldsymbol\\lambda_{1} \\boldsymbol{u_{1}^{\\top}} \\boldsymbol u_{2}=0 \\end{array}$
可知 $\\boldsymbol {u_1^{\\top}} \\boldsymbol u_2=0$ ，

则优化模型为
$\\begin{array}{l} \\max_{\\boldsymbol{u}_2 \\in\\mathbb R^{D}} \\operatorname{Var}\\left[y_{2}\\right]=\\boldsymbol {u}_{2}^{\\top} \\Sigma_{x} \\boldsymbol u_{2}\\\\ \\text { s.t. } \\;\\;\\boldsymbol {{u}_{2}^{\\top}} \\boldsymbol {u}_{2}=1 \\\\ \\qquad\\;\\;\\boldsymbol {{u}_{1}^{\\top}} \\boldsymbol {u}_{2}=0 \\end{array}$
构造拉格朗日函数
$\\mathcal{L}\\left(\\boldsymbol {u}_{2}, \\boldsymbol\\lambda_2,\\boldsymbol\\gamma \\right)=\\boldsymbol {{u}_{2}^{\\top}} {\\Sigma}_x \\boldsymbol {u}_{2}+\\boldsymbol\\lambda_{2}\\left(1-\\boldsymbol {{u}_{2}^{\\top}} \\boldsymbol {u}_{2}\\right)+\\boldsymbol\\gamma \\boldsymbol {{u}_{1}^{\\top}} \\boldsymbol {u}_{2}$
置偏导数为0，得
$\\frac{\\partial \\mathcal{L}\\left(\\boldsymbol u_{2}, \\boldsymbol\\lambda_{2}, \\boldsymbol\\gamma\\right)}{\\partial \\boldsymbol {u}_{2}}=2 {\\Sigma}_{x} \\boldsymbol {u}_{2}-2 \\boldsymbol\\lambda_{2} \\boldsymbol {u}_{2}+\\boldsymbol\\gamma \\boldsymbol {u}_{1}=\\ {0} \\tag{1}$

$\\frac{\\partial \\mathcal{L}\\left(\\boldsymbol {u}_{2}, \\boldsymbol\\lambda_{2}, \\boldsymbol\\gamma\\right)}{\\partial \\boldsymbol\\lambda_{2}}=1-\\boldsymbol {{u}_{2}^{\\top}} \\boldsymbol{u}_{2}=0$

$\\frac{\\partial \\mathcal{L}\\left(\\boldsymbol {u}_{2}, \\boldsymbol\\lambda_{2}, \\boldsymbol\\gamma\\right)}{\\partial \\boldsymbol\\gamma}=\\boldsymbol {{u}_{2}^{\\top}} \\boldsymbol{u}_{2}=0$

(1) 式两边同时左乘 $\\boldsymbol{{u}_{1}^{\\top}}$ 得
$\\begin{array}{l} 2 \\boldsymbol {{u}_{1}^{\\top}} \\Sigma_{x} \\boldsymbol {u}_{2}-2 \\boldsymbol\\lambda_{2} \\boldsymbol {{u}_{1}^{\\top}} \\boldsymbol {u}_{2}+\\boldsymbol\\gamma \\boldsymbol {{u}_{1}^{\\top}} \\boldsymbol {u}_{1}=0 \\\\ 2 \\boldsymbol\\lambda_{1} \\boldsymbol {{u}_{1}^{\\top}} \\boldsymbol {u}_{2}-2 \\boldsymbol\\lambda_{2} \\boldsymbol {{u}_{1}^{\\top}} \\boldsymbol {u}_{2}+\\boldsymbol\\gamma=0 \\end{array}$
即
$\\boldsymbol\\gamma=2\\left(\\boldsymbol\\lambda_{2}-\\boldsymbol\\lambda_{1}\\right) \\boldsymbol {{u}_{1}^{\\top}} \\boldsymbol {u}_{2}=0$
则 (1) 式可简化为
${\\Sigma}_ {\\boldsymbol x} \\boldsymbol {u}_{2}=\\boldsymbol\\lambda_{2} \\boldsymbol {u}_{2}$
说明最优解 $\\boldsymbol{u}_{2}$ 为协方差矩阵 $\\Sigma_{\\boldsymbol x}$ 的第二大特征值 $\\boldsymbol\\lambda_2$ 对应的特征向量，此时的极值
$\\max \\boldsymbol {{u}_{2}^{\\top}} {\\Sigma}_{x} \\boldsymbol u_2=\\boldsymbol\\lambda_{2} \\boldsymbol {{u}_{2}^{\\top}} \\boldsymbol {u}_{2}=\\boldsymbol\\lambda_{2}$
对于其余的主元 $y_i$ 与 $y_i(i\\not=j)$ 需满足 $y_{i}=\\boldsymbol{u}_i^{\\top}\\boldsymbol x$ 与 $y_{j}=\\boldsymbol {u}_{j}^{\\top}\\boldsymbol x$ 不相关，即
$\\operatorname{Cov}\\left( y_{i}, y_{j}\\right)=E\\left[\\boldsymbol {{u}_{i}^{\\top}} \\boldsymbol {x} \\boldsymbol{x^{\\top}}\\boldsymbol {u}_{j}\\right]=\\boldsymbol {{u}_{i}^{\\top}} \\ {\\Sigma}_x \\boldsymbol {u}_{j}=0$
假设 $\\boldsymbol {u}_{1}, \\boldsymbol {u}_{2}, \\cdots, \\boldsymbol {u}_{i-1}$ 为协方差矩阵 ${\\Sigma}_x$ 的最大 $i - 1$ 个归一化的特征向量，而最优解 $\\boldsymbol {u}_i$ 定义为第 $i$ 个主元 $\\boldsymbol y_i$ 对应的向量（未必为特征向量）。由前过程可知
$\\ {\\Sigma}_x \\boldsymbol {u}_{j}=\\boldsymbol\\lambda_{j} \\boldsymbol {u}_{j}\\qquad j=1,2, \\cdots, i-1$
且满足
$\\boldsymbol {u_i^{\\top}}\\ {\\Sigma}_{x} \\boldsymbol u_j = \\boldsymbol\\lambda_j \\boldsymbol {u_i^{\\top}} \\boldsymbol u_j = 0 \\qquad j=1,2, \\cdots, i-1,\\qquad \\lambda_j>0$
即
$\\boldsymbol{u_i^{\\top}} \\boldsymbol u_j=0 \\qquad j=1,2, \\cdots, i-1$
最优化模型为
$\\left\\{\\begin{array}{l} \\max Var[y_i] = \\boldsymbol u_i^{\\top} \\Sigma_{\\boldsymbol x} \\boldsymbol u_i \\\\ \\text { s.t. } \\boldsymbol u_i^{\\top} \\boldsymbol u_i=1\\\\ \\qquad \\boldsymbol u_i^{\\top} \\boldsymbol u_j = 0 \\qquad j = 1,2,\\cdots,i-1 \\end{array}\\right.$
构造拉格朗日函数
$\\mathcal{L}\\left(\\boldsymbol {u}_{i}, \\boldsymbol\\lambda_i,\\boldsymbol\\gamma_j \\right)=\\boldsymbol {{u}_{i}^{\\top}} {\\Sigma}_ x \\boldsymbol {u}_{i}+\\boldsymbol\\lambda_{i}\\left(1-\\boldsymbol {{u}_{i}^{\\top}} \\boldsymbol {u}_{i}\\right)+\\sum_{j=1}^{i-1}\\boldsymbol\\gamma_j \\boldsymbol {{u}_{i}^{\\top}} \\boldsymbol {u}_{j}$
置偏导数为0，得
$\\frac{\\partial \\mathcal{L}\\left(\\boldsymbol u_{i}, \\boldsymbol\\lambda_{i}, \\boldsymbol\\gamma_j\\right)}{\\partial \\boldsymbol {u}_{i}}=2 {\\Sigma}_{x} \\boldsymbol {u}_{i}-2 \\boldsymbol\\lambda_{i} \\boldsymbol {u}_{i}+\\sum_{j=1}^{i-1}\\boldsymbol\\gamma_j \\boldsymbol {u}_{j}=\\ {0}\\tag{2}$

$\\frac{\\partial \\mathcal{L}\\left(\\boldsymbol u_{i}, \\lambda_{i}, \\boldsymbol\\gamma_j\\right)}{\\partial \\ {\\lambda}_{i}}=1-\\boldsymbol {u_i^{\\top}} \\boldsymbol u_i = {0}$

$\\frac{\\partial \\mathcal{L}\\left(\\boldsymbol u_{i}, \\boldsymbol\\lambda_{i}, \\boldsymbol\\gamma_j\\right)}{\\partial \\ {\\boldsymbol\\gamma}_{j}}=\\boldsymbol{u_i^{\\top}} \\boldsymbol u_j = 0 \\qquad j = 1,2, \\cdots ,i-1$

(2)式两边同时左乘 $\\boldsymbol{u_j^{\\top}}$ ,得
$\\boldsymbol{2u_j^{\\top}} \\Sigma_ x \\boldsymbol u_i-2\\lambda_i \\boldsymbol {u_j^{\\top}} \\boldsymbol u_i + \\sum_{j=1}^{i-1} \\boldsymbol\\gamma_j \\boldsymbol u_j^{\\top} \\boldsymbol u_j=0 \\\\ 2\\lambda_j \\boldsymbol u_j^{\\top} \\boldsymbol u_i - 2\\lambda_j \\boldsymbol{u_j^{\\top}} \\boldsymbol u_i + \\sum_{j=1}^{i-1} \\boldsymbol\\gamma_j = 0$
即
$\\sum_{j=1}^{i-1} \\boldsymbol\\gamma_j = 2 \\left(\\lambda_j - \\lambda_i \\right) \\boldsymbol {u_j^{\\top}} \\boldsymbol u_i = 0$

由拉格朗日乘子 $\\boldsymbol\\gamma_j$ 非负，则 $\\boldsymbol\\gamma_j = 0 \\quad j = 1,\\cdots,i-1$ 。

(72) 式可简化为
$\\Sigma_ {\\boldsymbol x} \\boldsymbol u_i = \\boldsymbol\\lambda_i \\boldsymbol u_i$
即最优解 $\\boldsymbol u_i$ 为协方差矩阵 $\\Sigma_{\\boldsymbol x}$ 第 $i$ 个特征值 $\\lambda_i$ 对应的特征向量，此时的极值为
$\\text{max}\\;\\; \\boldsymbol {u_i^{\\top}} \\boldsymbol\\Sigma_x \\boldsymbol u_i = \\lambda_i \\boldsymbol {u_i^{\\top}} \\boldsymbol u_i = \\lambda_i = Var[y_i]$
对于 $\\Sigma_{\\boldsymbol x}$ 有重复特征根的情形亦如此，略。

由上述定理可知，随机变量 $\\boldsymbol x$ 的 $d$ 个主元要优于一个主元，将所有的 $d$ 个主元表示成一个向量
$\\boldsymbol{y}=\\begin{bmatrix} y_1\\\\ y_2 \\\\ \\vdots \\\\ y_d \\end{bmatrix} =\\begin{bmatrix} \\boldsymbol{u}_1^\\top\\boldsymbol{x}\\\\ \\boldsymbol{u}_2^\\top\\boldsymbol{x}\\\\ \\vdots \\\\ \\boldsymbol{u}_d^\\top\\boldsymbol{x}\\\\ \\end{bmatrix} =\\begin{bmatrix} \\boldsymbol{u}_1^\\top\\\\ \\boldsymbol{u}_2^\\top\\\\ \\vdots \\\\ \\boldsymbol{u}_d^\\top\\\\ \\end{bmatrix}\\boldsymbol{x} =U^\\top\\boldsymbol{x}$
其中 $\\boldsymbol y \\in R^d,U \\in R^{D\\times d}$ ,此时 $\\boldsymbol y$ 的协方差矩阵可表示为
$\\Sigma_{\\boldsymbol y} = E[\\boldsymbol y \\boldsymbol y^{\\top}] = E[U^{\\top}\\boldsymbol x\\boldsymbol x^{\\top}U] = U^{\\top} \\Sigma_{\\boldsymbol x} U$
满足 $U^{\\top}U = I_d$ 。

由线性代数知识可知，对于任意可对角化的矩阵 $A$ ，则存在由 $A$ 的特征向量组成的列表示的矩阵 $V$ ，有 $\\boldsymbol\\Lambda = V^{-1}AV$ ，而当矩阵 $A$ 是实对称半正定矩阵时，其特征值 $\\boldsymbol\\lambda_i \\ge 0$ ，特征向量互相正交，且 $V^{-1} = V^{\\top}$ 。因此，由于 $\\Sigma_x$ 是实对称正定矩阵，则方程 $\\Sigma_y = U^{\\top} \\Sigma_x U$ 中 $U$ 的列是协方差矩阵 $\\Sigma_x$ 的 $d$ 个特征向量组成。而 $\\Sigma_y$ 是一个对角矩阵，对角元为 $\\Sigma_x$ 的 $d$ 个特征值。因为我们的目标是极大化 $\\boldsymbol y_i$ 的方差 $Var[\\boldsymbol y_i] = \\lambda_i$ ，所以我们的结论是协方差矩阵 $\\Sigma_x$ 的前 $d$ 个最大特征值对应的特征向量做为 $U$ 的列，即为目标的最优解，其极值则为 $\\Sigma_y$ 的对角元上 $d$ 个特征值。

3. 非零均值随机变量的主元

当 $\\boldsymbol x \\in R^D$ 有非零均值，则 $\\boldsymbol x$ 的 $d$ 个不相关主元定义为
$y_i = \\boldsymbol {u_i^{\\top}} \\boldsymbol x + a_i \\qquad i = 1,2, \\cdots ,d$
满足
$\\boldsymbol{u_i^{\\top}} \\boldsymbol u_i = 1，Var(\\boldsymbol y_1) \\ge Var(\\boldsymbol y_2) \\ge \\cdots \\ge Var(\\boldsymbol y_d)>0$
由于随机变量 $y_i$ 满足
$\\mathbb E[y_i] = 0 \\\\ \\text{cov}(y_i,y_j) = 0 \\\\ \\mathbb E[y_i] = \\mathbb E[\\boldsymbol{u_i^{\\top}} \\boldsymbol x + a_i] = \\boldsymbol{u_i^{\\top}} \\mathbb E[\\boldsymbol x] + \\boldsymbol a_i = \\boldsymbol{u_i^{\\top}} \\boldsymbol\\mu_ x + a_i = 0 \\qquad i = 1,2, \\cdots ,d$
因此 $a_i = - \\boldsymbol{u_i^{\\top}} \\boldsymbol\\mu_x$

则
$Var[y_1] = Var[\\boldsymbol {u_1^{\\top}} \\boldsymbol x + a_1] = Var[\\boldsymbol {u_1^{\\top}} \\boldsymbol x - \\boldsymbol {u_1^{\\top}} \\boldsymbol\\mu_x] =Var[\\boldsymbol{u_1^{\\top}} \\left (\\boldsymbol x - \\boldsymbol\\mu_x \\right)] \\\\ = E[\\boldsymbol{u_1^{\\top}} (\\boldsymbol x - \\boldsymbol\\mu_x) (\\boldsymbol x - \\boldsymbol\\mu_x)^{\\top} \\boldsymbol u_1] = \\boldsymbol {u_1^{\\top}} E [(\\boldsymbol x - \\boldsymbol\\mu_x) (\\boldsymbol x - \\boldsymbol\\mu_x)^{\\top} ] \\boldsymbol u_1 = \\boldsymbol{u_1^{\\top}} \\Sigma_{\\boldsymbol x} \\boldsymbol u_1$
则最优解 $\\boldsymbol u_1$ 的计算可描述为 $\\text{max} \\ Var[y_1]$

即
$\\max_{\\boldsymbol u_1} \\boldsymbol {u_1^{\\top}} \\Sigma_x \\boldsymbol u_1 \\\\ \\boldsymbol{u_1^{\\top}} \\boldsymbol u_1 = 1$
构造拉格朗日函数
$\\mathcal{L}\\ (\\boldsymbol{u}_{1})=\\boldsymbol {{u}_{1}^{\\top}} {\\Sigma}_ {\\boldsymbol x} \\boldsymbol {u}_{1}+\\boldsymbol\\lambda_{i}\\left(1-\\boldsymbol {{u}_{1}^{\\top}} \\boldsymbol {u}_{1}\\right)$
置拉格朗日函数偏导数为0
$\\frac{\\partial \\mathcal{L} (\\boldsymbol u_{1})}{\\partial \\boldsymbol {u}_{1}}=2 {\\Sigma}_{x} \\boldsymbol {u}_{1}-2 \\boldsymbol\\lambda_{1} \\boldsymbol {u}_{1} = 0$
得
$\\Sigma_ x \\boldsymbol u_1 = \\lambda_1 \\boldsymbol u_1$
由此可知 $\\lambda_1$ 和 $\\boldsymbol u_1$ 分别为协方差矩阵 $\\Sigma_{\\boldsymbol x} = (\\boldsymbol x - \\boldsymbol\\mu ) (\\boldsymbol x - \\boldsymbol\\mu )^{\\top}$ 的最大特征值与其对应的特征向量。对于地 $i$ 个最优解 $\\boldsymbol u_i$ 的解与前面定理的证明完全一致。

4. 零均值随机变量的样本主元

在实际应用中，我们并不知道随机变量的协方差矩阵，只能由样本点进行估计，对于独立同分布且期望为0的样本 $\\left \\{ \\boldsymbol x_i \\right \\} _{i=1}^N$ ，构造样本矩阵 $\\boldsymbol X=[\\boldsymbol x_1,\\boldsymbol x_2, \\cdots ,\\boldsymbol x_N]$ ，其样本协方差为
$\\Sigma_N = \\frac{1}{N} \\sum_{i=1}^N \\boldsymbol x_i \\boldsymbol{x_i^{\\top}} = \\frac{1}{N} \\boldsymbol X \\boldsymbol{X^{\\top}}$
则 $d$ 个样本主元为
$y_i = \\boldsymbol{\\hat{u}_i^{\\top}} \\boldsymbol x \\qquad i = 1,2, \\cdots ,d$
其中 $\\left \\{ \\boldsymbol u_i \\right \\} _{i=1}^d$ 为 $\\hat\\Sigma_N = \\frac{1}{N} \\boldsymbol X \\boldsymbol{X^{\\top}}$ 或 $\\boldsymbol X \\boldsymbol{ X^{\\top} }$ 的前 $d$ 个特征向量。

由于 $\\boldsymbol X \\boldsymbol{X^{\\top}} \\in \\boldsymbol R^{D\\times D}$ 是一个非常大的矩阵，所以我们可以利用 $\\boldsymbol X$ 的奇异值获得最优解，即
$U_x \\Sigma_x V_x^{\\top}$

$\\boldsymbol{y}=\\begin{bmatrix} y_1\\\\ y_2 \\\\ \\vdots \\\\ y_d \\end{bmatrix} =\\begin{bmatrix} \\boldsymbol{u}_1^\\top\\boldsymbol{x}\\\\ \\boldsymbol{u}_2^\\top\\boldsymbol{x}\\\\ \\vdots \\\\ \\boldsymbol{u}_d^\\top\\boldsymbol{x}\\\\ \\end{bmatrix} =\\begin{bmatrix} \\boldsymbol{u}_1^\\top\\\\ \\boldsymbol{u}_2^\\top\\\\ \\vdots \\\\ \\boldsymbol{u}_d^\\top\\\\ \\end{bmatrix}\\boldsymbol{x} =U^\\top\\boldsymbol{x}$

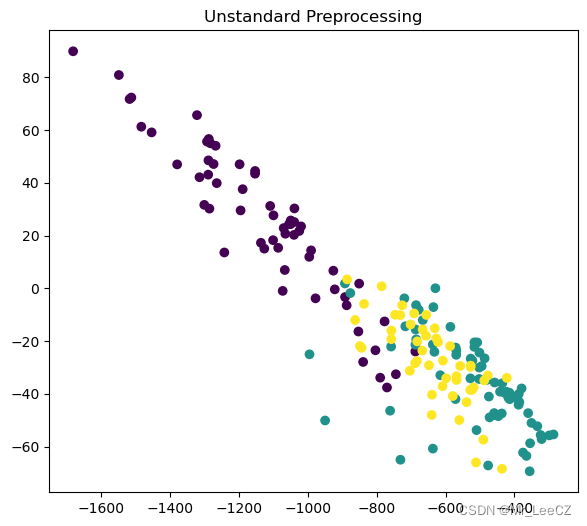
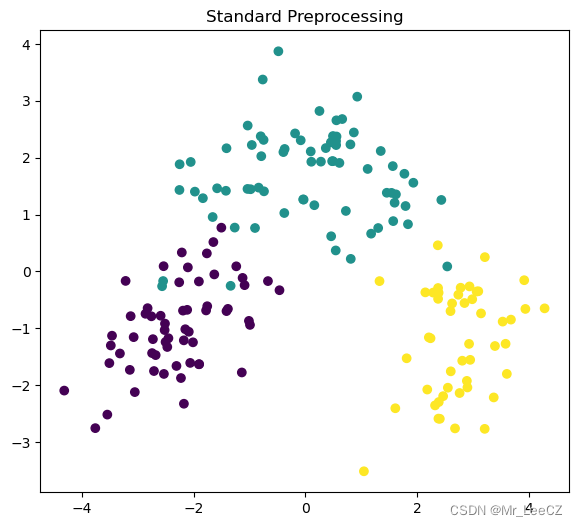
5. PCA 降维案例

We will first demonstrate PCA on a 13-dimensional dataset, by loading wine dataset from sklearn, see info here.

This dataset contains chemical analysis of N=178 different wines by three different cultivators.

The analysis contains the folowing measurements:

Alcohol
Malic acid
Ash
Alcalinity of ash
Magnesium
Total phenols
Flavanoids
Nonflavanoid phenols
Proanthocyanins
Colour intensity
Hue
OD280/OD315 of diluted wines
Proline

So overall, we have N=178 data points, lying in $\\mathbb{R}^{D}$ , with D=13. We stack all points together into a matrix X_wine $\\in \\mathbb{R}^{D\\times N}$ .

We have labels 0,1, or 2 for each wine (clutivator). The true labels are given in L_wine.

We want to see whether PCA can be helpful in the unsupervised task of clustering the 178 wines.

We start by loading the dataset, and printing the first 5 data points, just to get a general impression.

# 主成分分析算法
# 输入：
#      X: 数据矩阵大小为 n*D，每一行为 D 维向量（样本点）
# 参数：
#      dims_remain: 降维后保留的维数
#      with_std: 是否进行标准化操作，默认为进行标准化
# 返回：
#      X_reduction: 降维后的数据,数据矩阵大小为 n*d，每一行为 d 维向量（样本点）from numpy.linalg import svd
from sklearn.preprocessing import StandardScalerclass PCA_PC:def __init__(self,dims_remain=2,with_std=True):self.dims_remain = dims_remainself.with_std = with_stddef fit_transform(self,X):if self.with_std:ss = StandardScaler() # 此对象针对的是模式矩阵ss.fit(X)XS = ss.transform(X)U,_,_ = svd(XS.T) # 特征值分解函数的输入是模式矩阵的转置，输出 U 的每一列为新坐标轴X_reduction = XS@U[:,0:self.dims_remain]else:U,_,_ = svd(X.T)X_reduction = X@U[:,0:self.dims_remain]return X_reduction

调用函数

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_wineif __name__ == '__main__':     X_wine, L_wine = load_wine(return_X_y=True)np.set_printoptions(suppress=True)model1 = PCA_PC(dims_remain=2,with_std=False)X_reduct1 = model1.fit_transform(X_wine)plt.figure(figsize=(15,6))plt.subplot(121),plt.scatter(X_reduct1[:,0], X_reduct1[:,1], c=L_wine)plt.title('Unstandard Preprocessing')model2 = PCA_PC(dims_remain=2,with_std=True)X_reduct2 = model2.fit_transform(X_wine)plt.figure(figsize=(15,6))plt.subplot(121),plt.scatter(X_reduct2[:,0], X_reduct2[:,1], c=L_wine)plt.title('Standard Preprocessing')plt.show()

算法设计与智能计算 || 专题七: 主成分分析的统计学视角

算法设计与智能计算 || 专题七: 主成分分析的统计学视角

主成分分析的统计学视角

文章目录

PCA 的统计学视角

1. 寻找第一个主成分

2. 获取第二个主成分

3. 非零均值随机变量的主元

4. 零均值随机变量的样本主元

5. PCA 降维案例

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

标签

算法设计与智能计算 || 专题七: 主成分分析的统计学视角

主成分分析的统计学视角

文章目录

PCA 的统计学视角

1. 寻找第一个主成分

2. 获取第二个主成分

3. 非零均值随机变量的主元

4. 零均值随机变量的样本主元

5. PCA 降维案例

相关问题

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

标签