差分(一维+二维)

类似于数学中的求导和积分,差分可以看成前缀和的逆运算。
前缀和我们是求原数组的前缀和,这里是把原数组当成前缀和,构造一个差分数组来运算
以一维为例,如原数组为a[1],a[2],a[3]...a[n]
前缀和的思想是构造st[1]=a[1],st[2]=a[1]+a[2],st[3]=a[1]+a[2]+a[3],...,st[n]=a[1]+a[2]+...+a[n]
而差分则是构造a[1]=b[1],a[2]=b[1]+b[2],a[3]=b[1]+b[2]+b[3],...,a[n]=b[1]+b[2]+...+b[n]
这样的好处是啥呢,后面以一维和二维的题来展示
1.一维差分
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数l,r,c,表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 m 行,每行包含三个整数l,r,c,表示一个操作。
输出格式
共一行,包含 n 个整数,表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2一开始写这道题时,最容易想到的就是循环一遍把每一个位置加上该数,但是后面发现时间复杂度太大O(n)数据过不了,如果运用差分我们就可以做到O(1)的复杂度,即在差分数组中通过使某几个点加入该数,使得原数组大面积随之变化,优化时间
这里有一篇带图文章写的非常好,链接放这不懂得可以看看AcWing 797. 差分 【c++详细题解】 - AcWing
代码实现:
#include<iostream>
using namespace std;
const int N=100010;
int arr[N],st[N];
int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++) scanf("%d",&arr[i]),st[i]=arr[i]-arr[i-1];while(m--){int l,r,c;scanf("%d%d%d",&l,&r,&c);st[l]+=c,st[r+1]-=c;}for(int i=1;i<=n;i++){arr[i]=arr[i-1]+st[i];printf("%d ",arr[i]);}return 0;
}2.二维差分
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 cc。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2二维差分的主要思维就是如何运用差分数组通过O(1)的时间复杂度来使原数组某个矩阵所有元素加一,正常如果靠循环就是O(n*n)的复杂度,如何用O(1)的复杂度实现呢?
这里给出图片
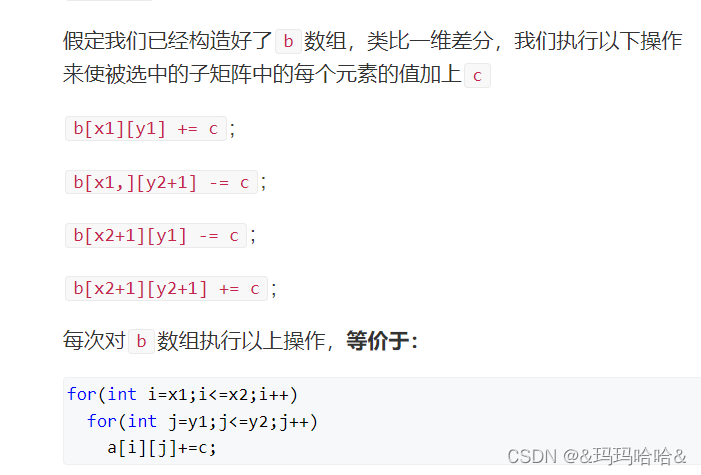
通过这样一个数组的运算就可以使给定矩阵范围内每一个数加c,且时间复杂度为O(1),如果仍然不懂这里提供更详细解释的链接(AcWing 798. 差分矩阵 【 c++详细题解 】 - AcWing),这里就直接给代码了
代码实现:
#include<iostream>
using namespace std;
const int N=1010;
int arr[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c)//设置插入函数来构造差分数组
{b[x1][y1]+=c;b[x2+1][y1]-=c;b[x1][y2+1]-=c;b[x2+1][y2+1]+=c;
}int main()
{int n,m,q;scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++) cin>>arr[i][j],insert(i,j,i,j,arr[i][j]);//构建差分数组while(q--){int x1,y1,x2,y2,c;scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);insert(x1,y1,x2,y2,c);}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];//把差分函数通过前缀和运算得到加完后的数组printf("%d ",b[i][j]);}printf("\\n");}return 0;
}
