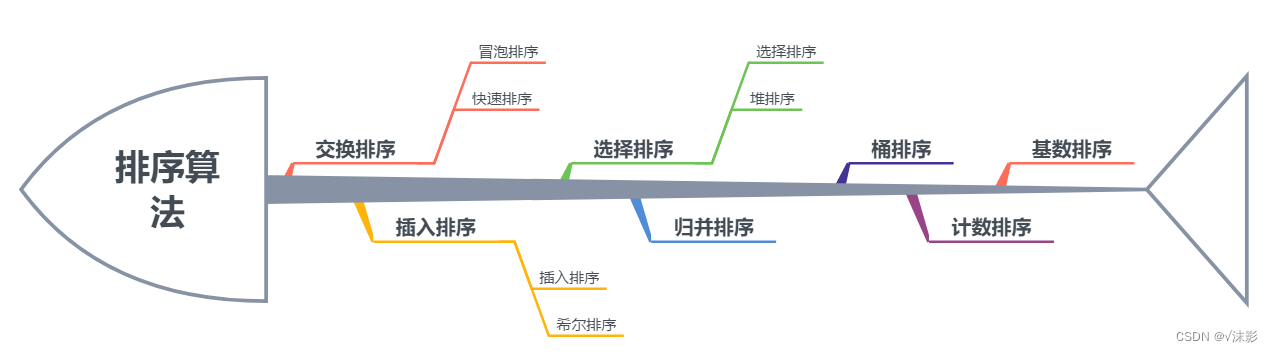
C++算法:排序、查找

排序
排序是一个非常经典的问题,它以一定的顺序对一个数组(或一个列表)中的项进行重新排序
有许多不同的排序算法,每个都有其自身的优点和局限性。
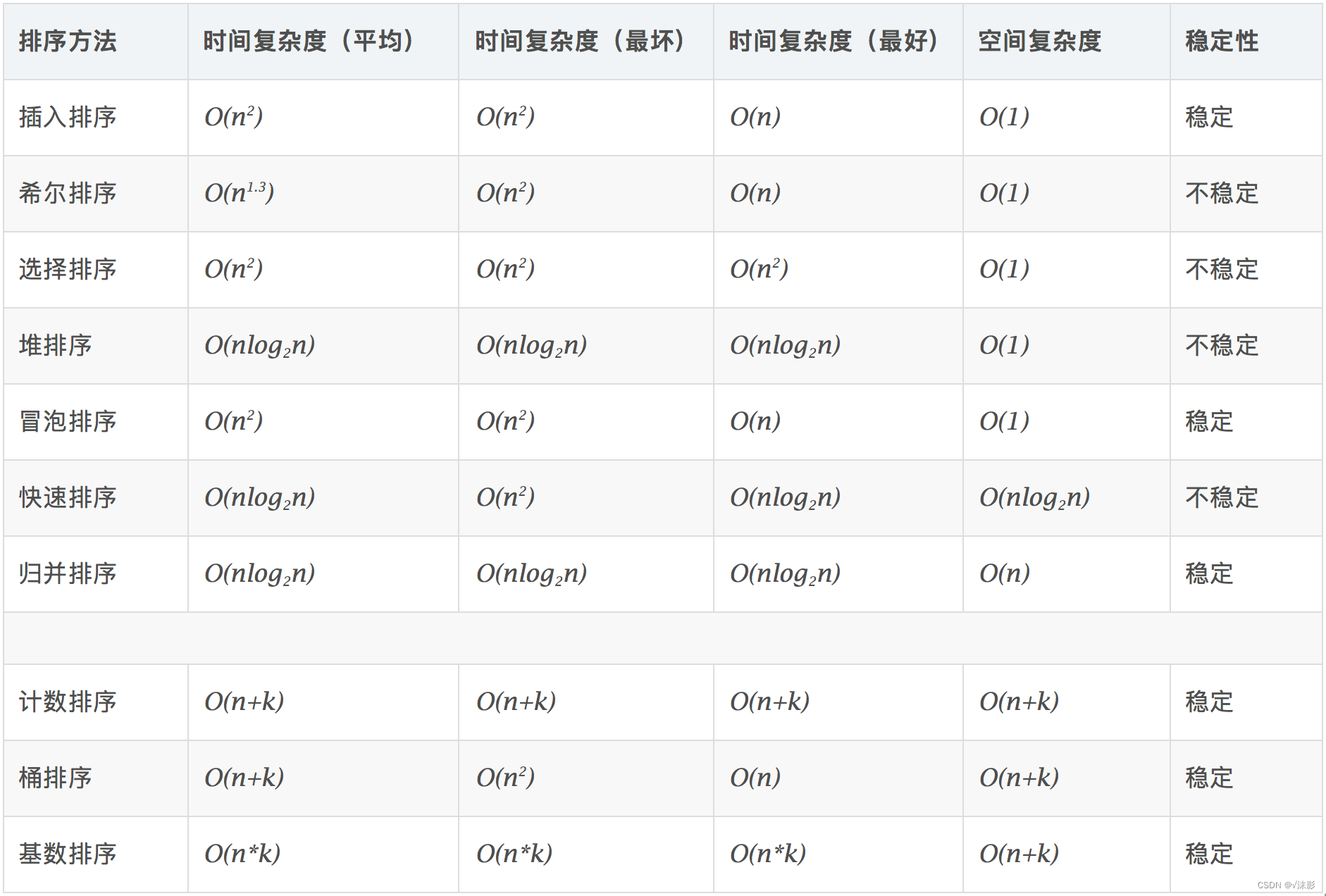
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
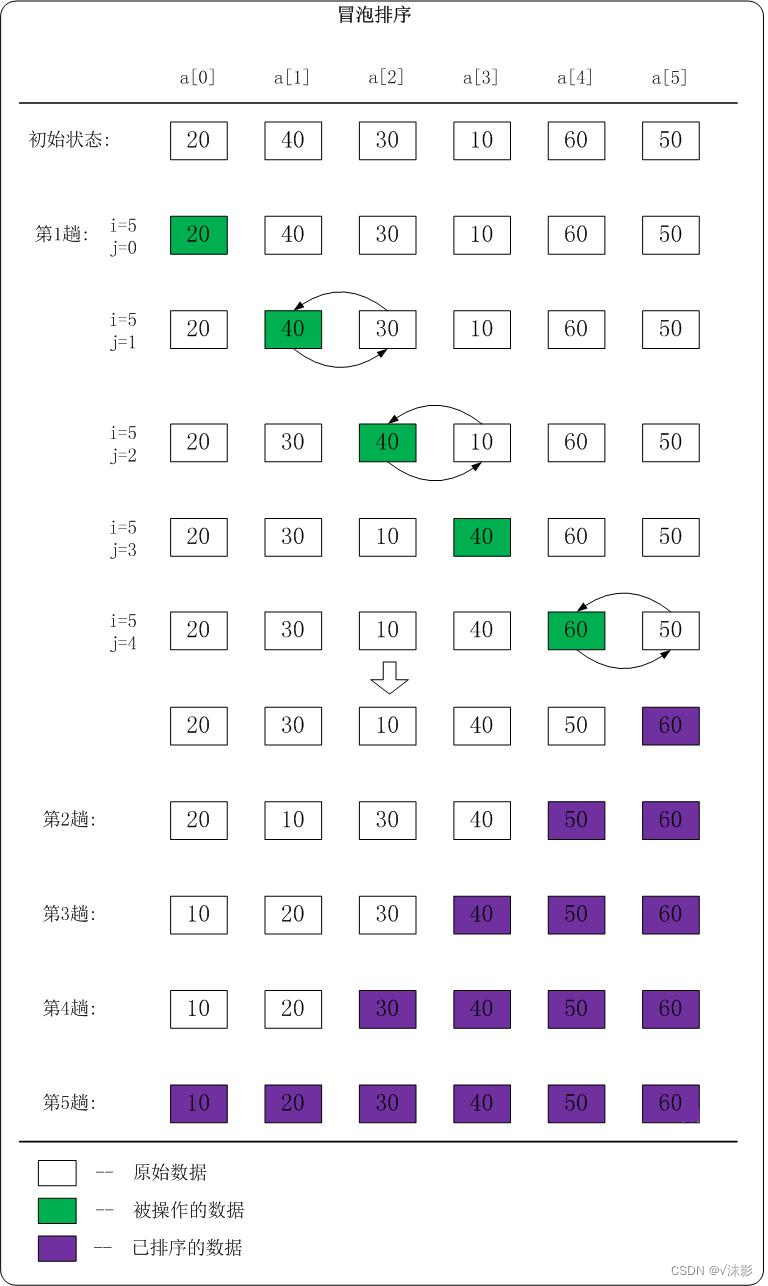
冒泡排序
- 比较相邻的元素。如果元素大小关系不正确,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
#pragma region 冒泡排序
/*
1.比较相邻的元素。如果元素大小关系不正确,就交换它们两个;
2.对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对;
3.针对所有的元素重复以上的步骤,除了最后一个;
4.重复步骤1~3,直到排序完成。
*/
void BubbleSort1(int* arr, int size)
{for (int i = 0; i < size - 1;++i)for(int j=0;j<size-1-i;++j)if (arr[j]>arr[j + 1])std::swap(arr[j], arr[j + 1]);
}void BubbleSort2(int* arr, int size)//改进版
{bool flag;for (int i = 0; i < size - 1; ++i){flag = false;for (int j = 0; j < size - 1 - i; ++j){if (arr[j]>arr[j + 1]){std::swap(arr[j], arr[j + 1]);flag = true;}}if (!flag)break; //如果没有发生交换,说明数组已经有序}
}#pragma endregion
快速排序
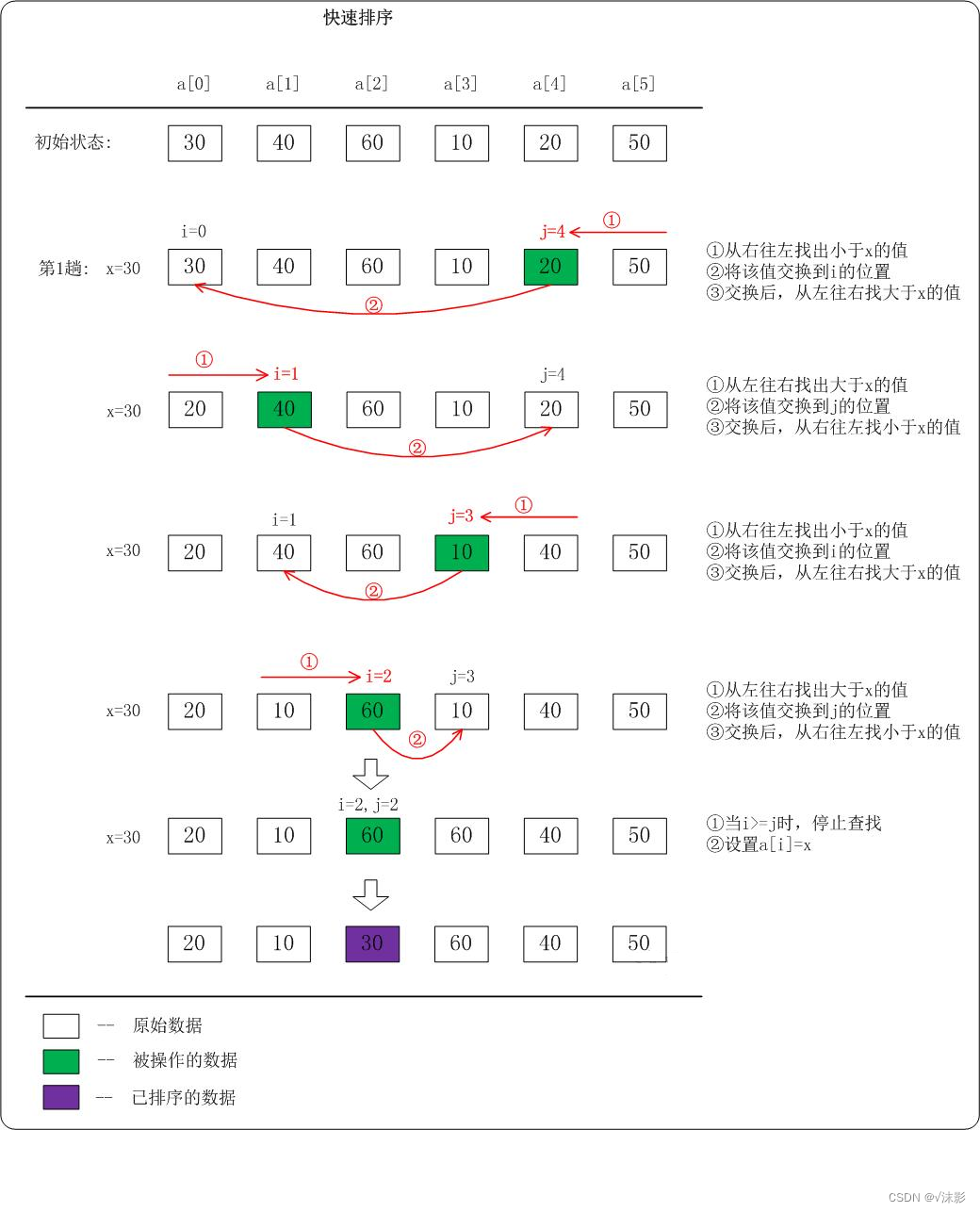
- 从待排序序列中挑出一个元素,作为”基准”;
- 把所有比基准值小的元素放在基准前面,所有比基准值大的元素放在基准的后面(相同的数可以到任一边),这个过程叫分组或分区
- 递归地把”基准值前面的子数列”和”基准值后面的子数列”进行排序。不多于一个为止
#pragma region 快速排序
/*
1.从待排序序列中挑出一个元素,作为”基准”;
2.把所有比基准值小的元素放在基准前面,所有比基准值大的元素放在基准的后面(相同的数可以到任一边),这个过程叫分组或分区
3.递归地把”基准值前面的子数列”和”基准值后面的子数列”进行排序。不多于一个为止
*/void QuickSort(int *arr, int start, int end)
{//分区if (start < end){int i, j, p;i = start;j = end;p = arr[i];while (i < j){while (i < j&& arr[i] < p)i++; //从左往右找第一个大于p的数if (i < j)arr[j--] = arr[i];while (i<j&& arr[j]>p)j--; //从右往左找第一个小于p的数if (i < j)arr[i++] = arr[j];}arr[i] = p;QuickSort(arr, start, i - 1);QuickSort(arr, i + 1, end);}
}
#pragma endregion
插入排序
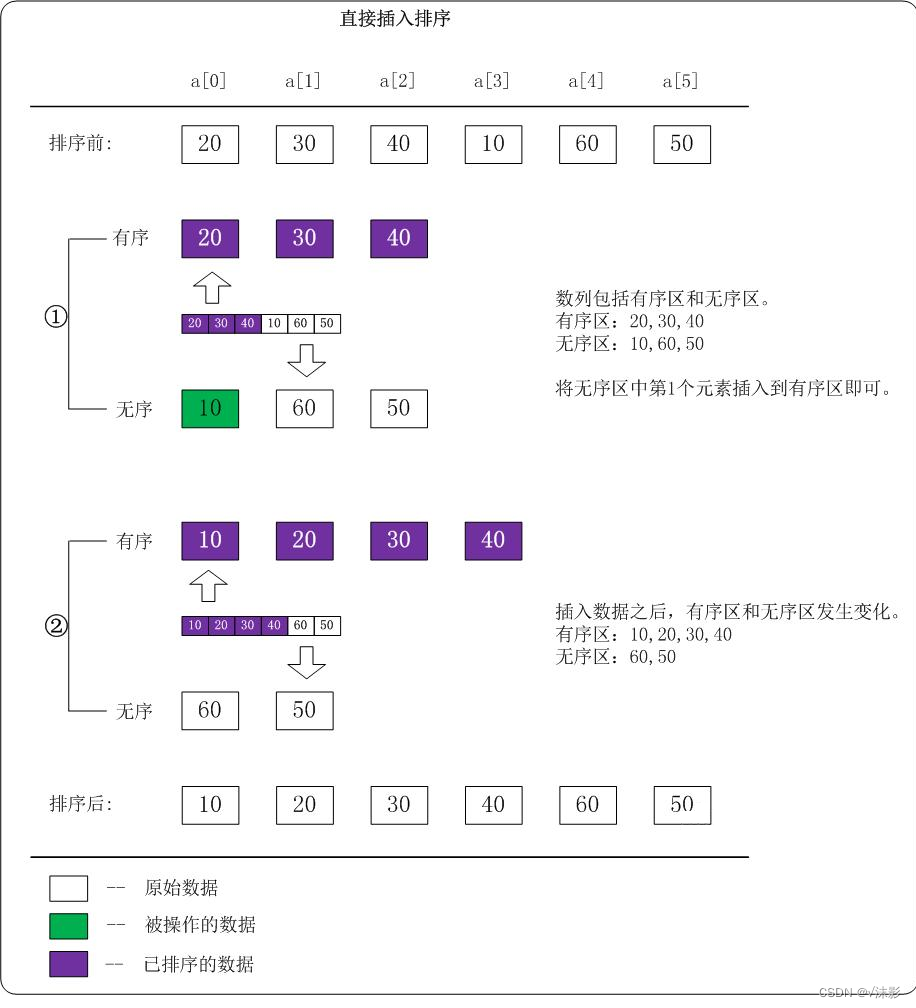
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
#pragma region 插入排序
void InsertSort(int* arr, int size)
{int temp;int j;for (int i = 1; i < size; ++i){temp = arr[i];j = i - 1;while (j >= 0 && arr[j] > temp){arr[j + 1] = arr[j];j--;}arr[j + 1] = temp;}
}#pragma endregion
桶排序
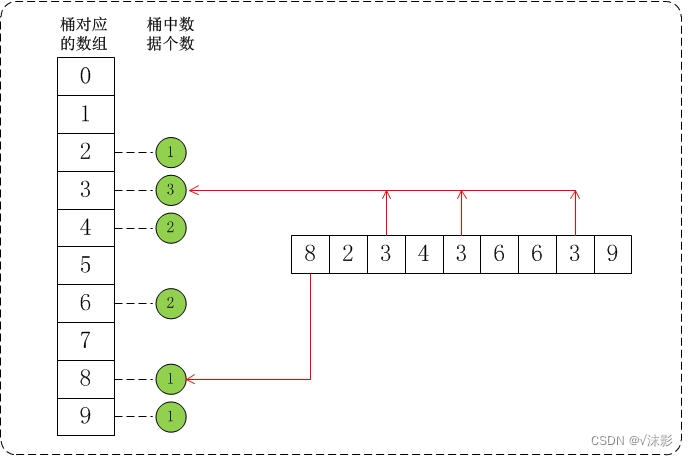
- 设置一个定量的数组当作空桶;
- 遍历输入数据,并且把数据一个一个放到对应的桶里去;
- 对每个不是空的桶进行排序;
- 从不是空的桶里把排好序的数据拼接起来。
#pragma region 桶排序
void BucketSort(int* arr, int size, int max)
{//创建一个容量为max的数组buckets,并且将buckets中所有数据都初始化为0vector<int> buckets(max);//1.计数for (int i = 0; i < size; ++i)buckets[arr[i]]++;//2.排序for (int i = 0, j = 0; i < max; ++i){while (buckets[i]>0){arr[j] = i;j++;buckets[i]--;}}
}#pragma endregion
希尔排序
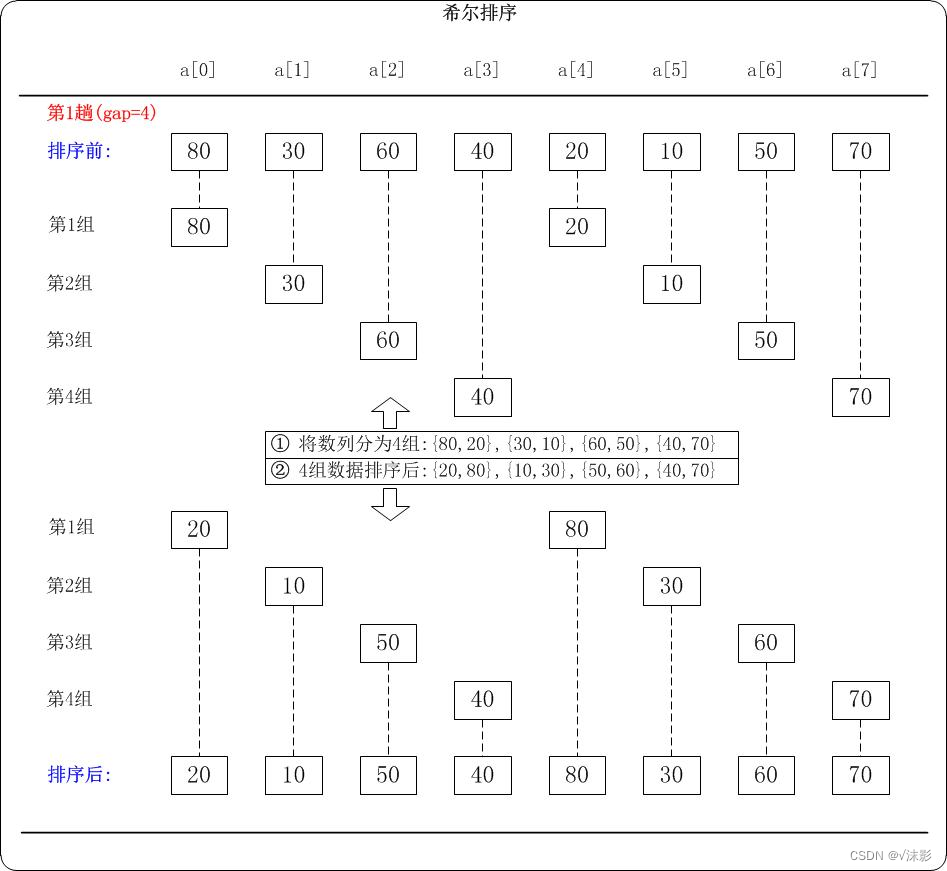
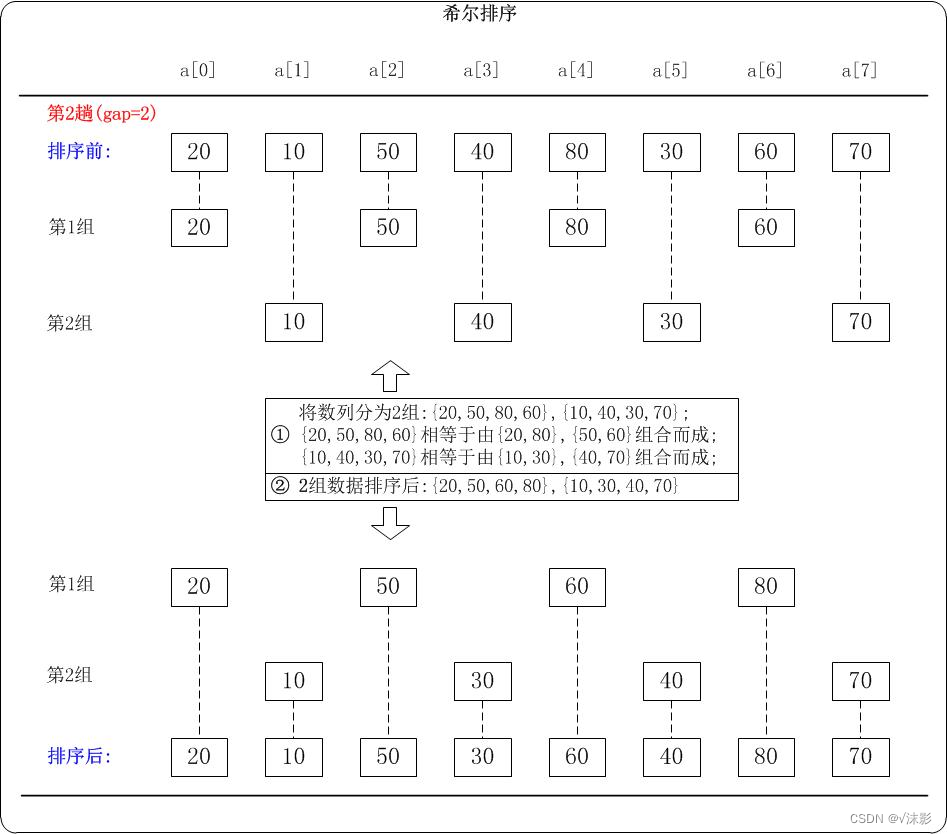
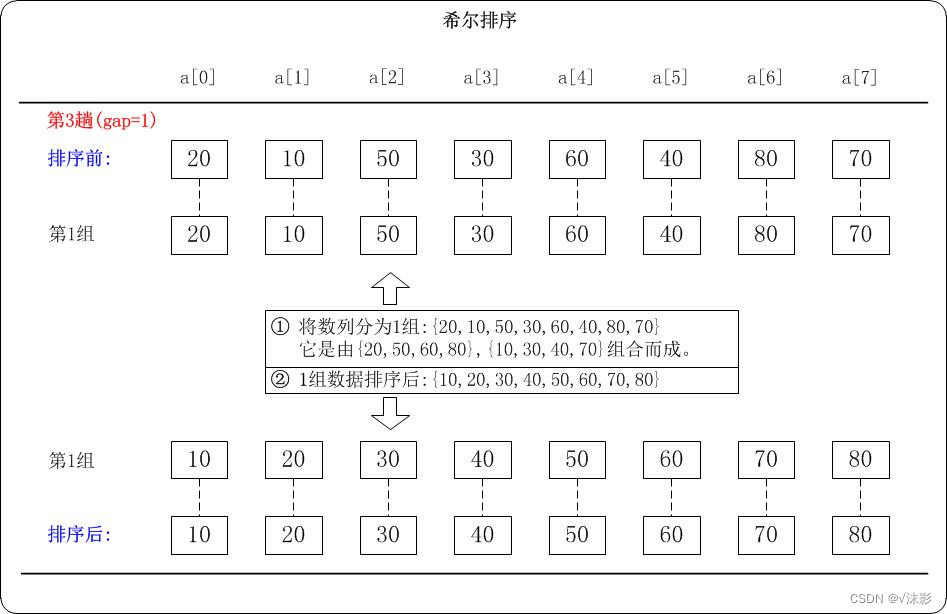
- 对于n个待排序的数列,取一个小于n的整数gap(gap被称为步长)将待排序元素分成若干个组子序列,所有距离为gap的倍数的记录放在同一个组中;
- 对各组内的元素进行直接插入排序,这一趟排序完成之后,每一个组的元素都是有序的;
- 减小gap的值,并重复执行上述的分组和排序,当gap=1时,整个数列就是有序的。
#pragma region 希尔排序
//基于插入排序
void ShellSort(int* arr, int size)
{int temp;int j;//gap为步长 每次减为原来的一半for (int gap = size / 2; gap > 0; gap /= 2){for (int i = gap; i < size; ++i){temp = arr[i];j = i - gap;while (j >= 0 && arr[j] > temp){arr[j + gap] = arr[j];j -= gap;}arr[j + gap] = temp;}}
}
#pragma endregion
选择排序
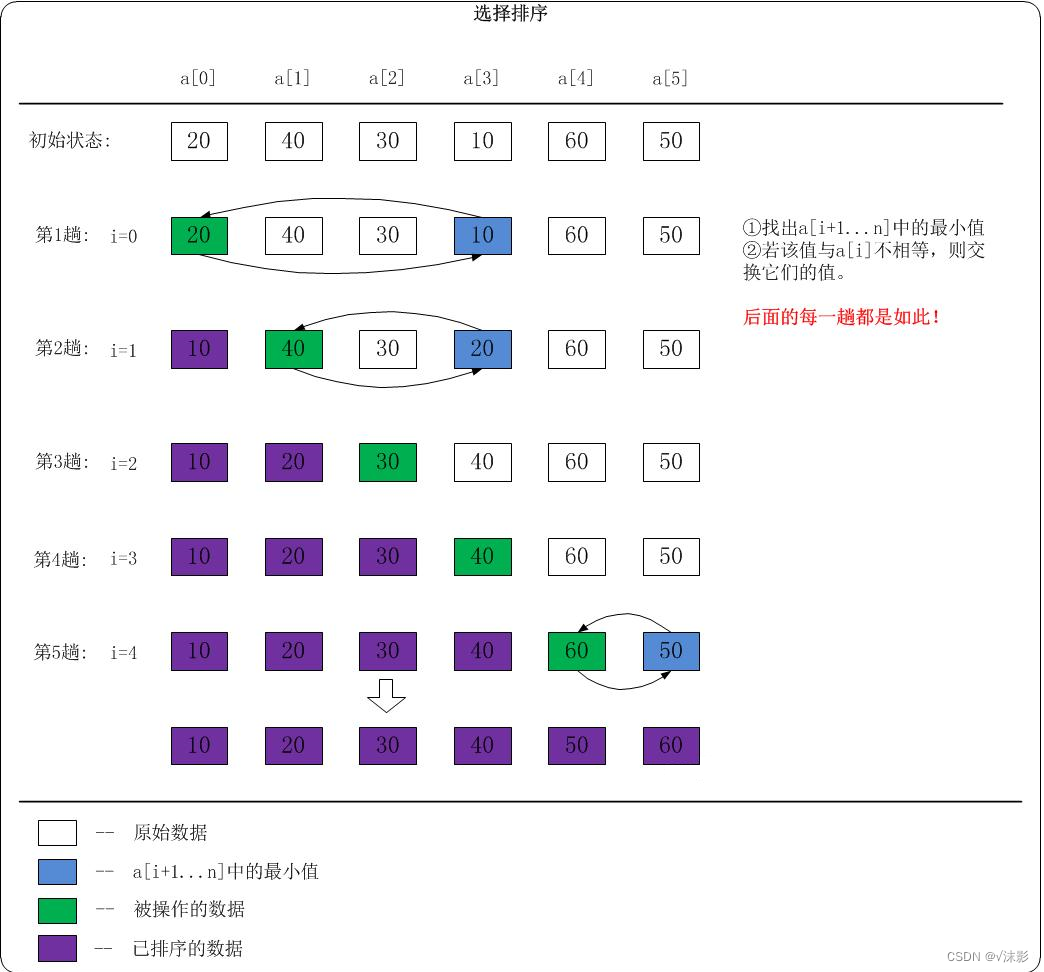
- 未排序的数列中找到最小(or最大)元素,然后将其存放到数列的起始位置;
- 从剩余未排序的元素中继续寻找最小(or最大)元素,然后放到已排序序列的末尾;
- 以此类推,直到所有元素均排序完毕;
#pragma region 选择排序
void SelectionSort(int* arr, int size)
{for (int i = 0; i < size - 1; ++i)//有序区的末尾位置for (int j = i + 1; j < size; ++j)//无序区if (arr[i]>arr[j])swap(arr[i], arr[j]);
}
#pragma endregion
归并排序
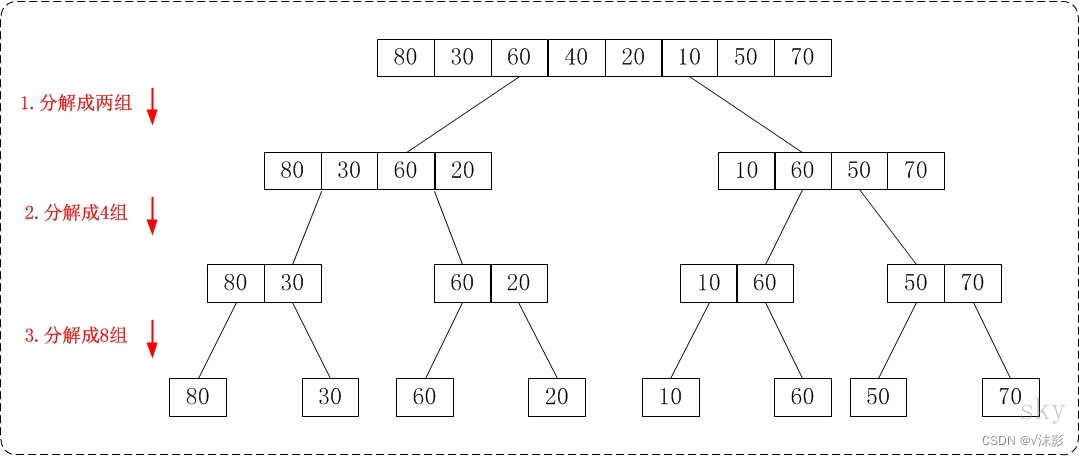
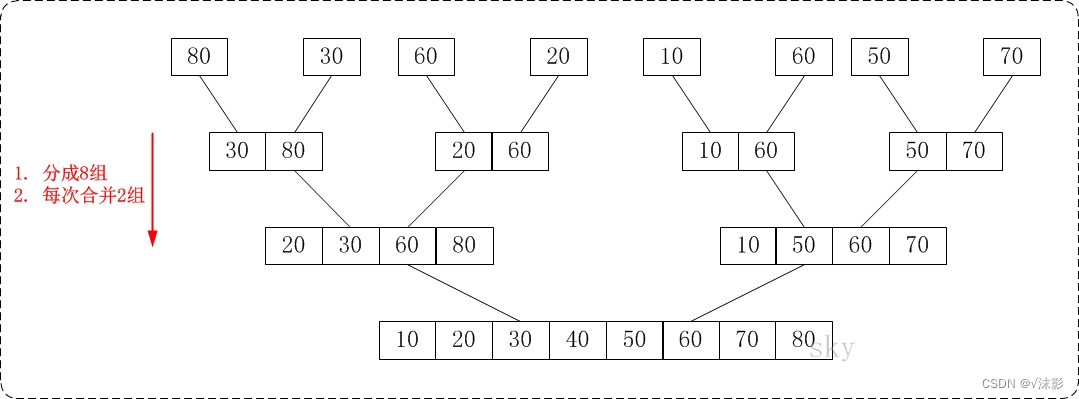
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
#pragma region 归并排序void Merge(int* arr, int left, int mid, int right)
{int low = left;//左半部分起始位置 (low,mid) int hight = mid + 1;//右半部分起始位置 (hight,right)int len = right - left + 1;vector<int> temp(len);//辅助数组int index = 0;//辅助数组下标while (low <= mid && hight <= right){//挑选两部分最小的元素放到辅助数组中if (arr[low] < arr[hight]){temp[index] = arr[low];low++;index++;}else{temp[index] = arr[hight];hight++;index++;}}//剩余直接放到辅助数组中while (low <= mid){temp[index] = arr[low];index++;low++;}while (hight <= right){temp[index] = arr[hight];index++;hight++;}//更新原始左边的元素for (int i = 0; i < len; ++i){arr[left + i] = temp[i];}
}void MergeSort(int* arr, int left, int right)
{if (left < right){int mid = (left + right) / 2; //分割MergeSort(arr, left, mid); //对左半部分进行归并MergeSort(arr, mid + 1, right);//对右半部分进行归并Merge(arr, left, mid, right);}
}
#pragma endregion
查找
根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素
顺序查找
关键字与队列中的数从最后一个开始逐个比较,直到找出与给定关键字相同的数为止
#pragma region 顺序查找
int SequenceSearch(int* arr, int len, int val)
{for (int i = 0; i < len; ++i){if (val == arr[i]){return i;}}return -1;
}#pragma endregion
- 缺点:效率低下
- 时间复杂度:最坏情况下,关键词比较次数为n+1,最好情况就是1,所以时间复杂度为O(logn)
二分查找
首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。\\
#pragma region 二分查找
int BinarySearch(int* arr, int val, int low, int high)
{int mid = (high + low) / 2;if (arr[mid] == val)return mid;if (arr[mid] > val)return BinarySearch(arr, val, low, mid - 1);if (arr[mid] < val)return BinarySearch(arr, val, mid + 1, high);
}int BinarySearch1(int* arr, int val, int low, int high)
{int mid;while (low <= high){mid = (low + high) / 2;if (arr[mid] == val)return mid;if (arr[mid] > val)high = mid - 1;if (arr[mid] < val)low = mid + 1;}return -1;
}#pragma endregion
- 缺点:要求待查表为有序表
- 时间复杂度:最坏情况下,关键词比较次数为,最好情况就是1,所以二分查找的时间复杂度为o(lob2n)
插值查找
基于二分查找算法,将查找点的选择改进为自适应选择,可以提高查找效率
#pragma region 插值查找
int InsertionSearch(int* arr, int val, int low, int high)
{// arr[index]=val;// (index-low)/ (val-arr[low])//= (high-low)/(arr[high]-arr[low])int index = low + (val - arr[low]) / (arr[high] - arr[low]) *(high - low);if (arr[index] == val)return index;if (arr[index] > val)return BinarySearch(arr, val, low, index - 1);if (arr[index] < val)return BinarySearch(arr, val, index + 1, high);
}#pragma endregion
降序排序
//冒泡降序
void BubbleSort2(int* arr, int size)//改进版
{bool flag = false;for (int i = 0; i < size - 1; ++i){flag = false;for (int j = 0; j < size - 1 - i; ++j){if (arr[j] < arr[j + 1]){std::swap(arr[j], arr[j + 1]);flag = true;}}if (!flag)break; // 若没发生交换,则说明数列已有序。}
}//快速降序
void QuickSort(int* arr, int left, int right)
{if (left < right){int i, j, p;i = left;j = right;p = arr[i];while (i < j){while (i < j && arr[j] < p)j--; // 从右向左找第一个大于x的数if (i < j)arr[i++] = arr[j];while (i < j && arr[i] > p)i++; // 从左向右找第一个小于x的数if (i < j)arr[j--] = arr[i];}arr[i] = p;QuickSort(arr, left, i - 1); /* 递归调用 */QuickSort(arr, i + 1, right); /* 递归调用 */}
}
//插入降序
void InsertSort(int* arr, int size)
{int temp;int j;for (int i = 1; i < size; i++){temp = arr[i];j = i - 1;while (j >= 0 && arr[j] < temp){arr[j + 1] = arr[j];j--;}arr[j + 1] = temp;}
}
//桶排序降序
void BucketSort(int* arr, int size, int max)
{int i, j;// 创建一个容量为max的数组buckets,并且将buckets中的所有数据都初始化为0。vector<int> buckets(max);// 1. 计数for (i = 0; i < size; i++)buckets[arr[i]]++;// 2. 排序for (i = max - 1, j = 0; i >= 0; i--)while ((buckets[i]--) >0)arr[j++] = i;
}